 Technology peripherals
Technology peripherals
 AI
AI
 Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?
Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?
Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?
Written in front&The author’s personal understanding
Three-dimensional Gaussian splatting (3DGS) is a revolutionary technology that has emerged in the fields of explicit radiation fields and computer graphics in recent years. This innovative method is characterized by the use of millions of 3D Gaussians, which is very different from the neural radiation field (NeRF) method, which mainly uses an implicit coordinate-based model to map spatial coordinates to pixel values. With its explicit scene representation and differentiable rendering algorithms, 3D GS not only guarantees real-time rendering capabilities, but also introduces an unprecedented level of control and scene editing. This positions 3D GS as a potential game-changer for next-generation 3D reconstruction and representation. To this end, we provide the first systematic overview of the latest developments and key contributions in the field of 3D GS. First, the basic principles and formulas for the emergence of 3D GS are explored in detail, laying the foundation for understanding its significance. Then the practicality of 3D GS is discussed in depth. By facilitating real-time performance, 3D GS opens up a host of applications, from virtual reality to interactive media and more. In addition, a comparative analysis of leading 3D GS models is conducted and evaluated on various benchmark tasks to highlight their performance and practicality. The review concludes by identifying current challenges and suggesting potential avenues for future research in this area. With this survey, we aim to provide both newcomers and experienced researchers with a valuable resource, stimulating further exploration and advancement in applicable and unambiguous representations of radiation fields.
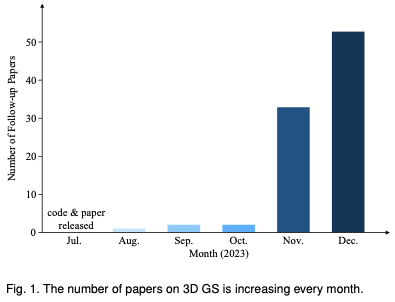
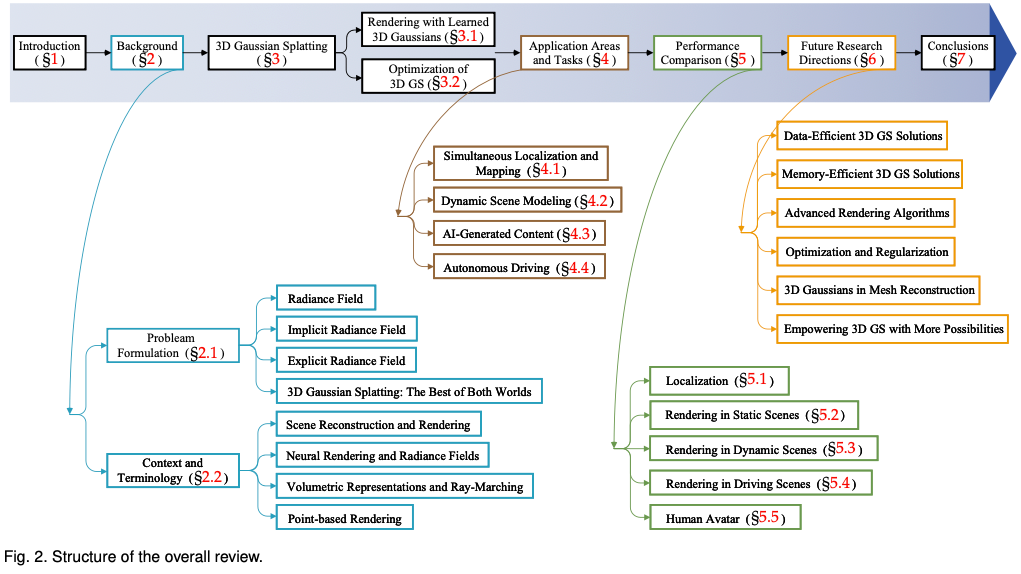
To help readers keep up with the rapid development of 3D GS, we provide the first survey review on 3D GS. We have systematically and timely collected the most important latest literature on this topic, mainly from arxiv. The goal of this article is to provide a comprehensive and up-to-date analysis of the initial development, theoretical foundations, and emerging applications of 3D GS, highlighting its revolutionary potential in the field. Given the nascent but rapidly evolving nature of 3D GS, this survey also aims to identify and discuss current challenges and future prospects in this field. We provide insights into ongoing research directions and potential advances that 3D GS may facilitate. It is hoped that this review will not only provide academic knowledge but also stimulate further research and innovation in this field. The structure of this article is as follows: (Figure 2) Please note that all content is based on the latest literature and research results and aims to provide readers with comprehensive and timely information about 3D GS.
Background introduction
This section introduces the brief formula of the radiation field, which is a key concept in scene rendering. Radiation fields can be represented by two main types: implicit, like NeRF, which uses neural networks for direct but computationally demanding rendering; and explicit, like meshes, which employ discrete structures for faster access but less memory Higher usage. Next, we will further explore the connections to related areas such as scene reconstruction and rendering.
Problem Definition
Radiation field: A radiation field is a representation of the distribution of light in three-dimensional space. It captures how light interacts with surfaces in the environment and Material interactions. Mathematically, a radiation field can be described as a function that maps a point in space and a direction specified by spherical coordinates to non-negative radiation values. Radiation fields can be encapsulated by implicit or explicit representations, each of which has specific scene representation and rendering advantages.
Implicit radiation field: The implicit radiation field represents the light distribution in the scene without explicitly defining the geometry of the scene. In the era of deep learning, it often uses neural networks to learn continuous volumetric scene representations. The most prominent example is NeRF. In NeRF, an MLP network is used to map a set of spatial coordinates and viewing directions to color and density values. The radiance of any point is not stored explicitly but is calculated in real time by querying the neural network. Therefore, the function can be written as:
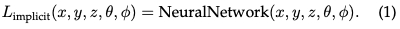
This format allows a compact, differentiable representation of complex scenes, although the computational load during rendering is higher due to the volume Light travels.
Explicit Radiation Field: In contrast, an explicit radiation field directly represents the light distribution in a discrete spatial structure, such as a grid of voxels or a set of points. Each element in the structure stores radiation information for its corresponding position in space. This approach allows more direct and often faster access to radiometric data, but at the cost of higher memory usage and potentially lower resolution. The general form of explicit radiation field representation can be written as:
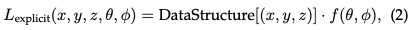
The DataStructure can be a grid or a point cloud, which is a function that modifies radiation based on the viewing direction.
The best of both worlds 3D Gaussian Splatting: 3D GS represents the transition from an implicit radiation field to an explicit radiation field. It exploits the advantages of both methods by leveraging 3D Gaussians as a flexible and efficient representation. These Gaussian coefficients are optimized to accurately represent the scene, combining the advantages of neural network-based optimization and explicit structured data storage. This hybrid approach aims to achieve high-quality rendering with faster training and real-time performance, especially for complex scenes and high-resolution output. The 3D Gaussian representation is formulated as:
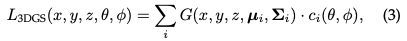
Context and Terminology
Many technologies and research disciplines are closely related to 3D GS, as follows It will be briefly described.
Scene Reconstruction and Rendering: Roughly speaking, scene reconstruction involves creating a 3D model of a scene from a collection of images or other data. Rendering is a more specific term that focuses on converting computer-readable information (for example, 3D objects in a scene) into pixel-based images. Early techniques were based on light fields to generate realistic images. Structure-from-motion (SfM) and multi-view stereo (MVS) algorithms further advance the field by estimating 3D structure from image sequences. These historical methods laid the foundation for more complex scene reconstruction and rendering techniques.
Neural Rendering and Radiant Fields: Neural rendering combines deep learning with traditional graphics techniques to create photorealistic images. Early attempts used convolutional neural networks (CNNs) to estimate hybrid weights or texture space solutions. A radiation field represents a function that describes the amount of light traveling in each direction through each point in space. NeRFs uses neural networks to model radiation fields, enabling detailed and realistic scene rendering.
Volume Representation and Ray-Marching: Volume representation models targets and scenes not only as surfaces, but also as volumes filled with materials or empty space. This method allows for more accurate rendering of phenomena such as fog, smoke, or translucent materials. Ray-Marching is a technique used with volumetric representations to render images by incrementally tracing the path of light through a volume. NeRF shares the same spirit of volumetric ray marching and introduces importance sampling and positional encoding to improve the quality of synthesized images. While providing high-quality results, volume ray traveling is computationally expensive, prompting the search for more efficient methods such as 3D GS.
Point-based rendering: Point-based rendering is a technique for visualizing 3D scenes using points instead of traditional polygons. This approach is particularly effective for rendering complex, unstructured, or sparse geometric data. Points can be enhanced with additional properties, such as learnable neural descriptors, and rendered efficiently, but this approach may suffer from issues such as holes or aliasing effects in rendering. 3D GS extends this concept by using anisotropic Gaussians to achieve a more continuous and cohesive representation of the scene.
3D Gaussian for Explicit Radiation Fields
3D GS is a breakthrough in real-time, high-resolution image rendering without relying on neural components.
Learned 3D Gaussians for new perspective synthesis
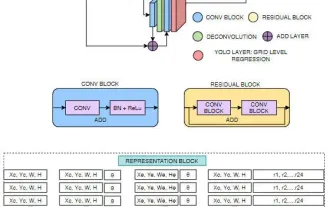
Consider a scene represented by (millions of) optimized 3D Gaussians. The goal is to generate an image based on a specified camera pose. Recall that NeRF accomplishes this task by computationally demanding volumetric ray travel, sampling a 3D space point for each pixel. This mode makes it difficult to achieve high-resolution image synthesis and cannot achieve real-time rendering speed. In stark contrast, 3D GS first projects these 3D Gaussians onto a pixel-based image plane, a process called “splatting” (Fig. 3a). 3D GS then sorts these Gaussians and calculates the value of each pixel. As shown in the figure, the rendering of NeRF and 3D GS can be viewed as the inverse processes of each other. In what follows, we start with the definition of a 3D Gaussian, which is the smallest element of scene representation in a 3D GS. Next we describe how to use these 3D Gaussians for differentiable rendering. Finally, the acceleration technology used in 3D GS is introduced, which is the key to fast rendering.
Properties of three-dimensional Gaussian: The characteristics of three-dimensional Gaussian are its center (position) μ, opacity α, three-dimensional covariance matrix ∑ and color c. For view-dependent appearance, c is represented by the spherical harmonics. All attributes are learnable and optimized via backpropagation.
Frustum Culling: Given a specified camera pose, this step determines which 3D Gaussians lie outside the camera's frustum. By doing this, 3D Gaussians outside a given view will not be involved in subsequent calculations, thus saving computational resources.
Splatting: **In this step, the 3D Gaussian (ellipsoid) is projected into the 2D image space (ellipsoid) for rendering. Given a viewing transformation W and a 3D covariance matrix Σ, the projected 2D covariance matrix Σ′ is calculated using the following formula:
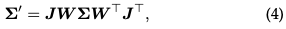
where J is the Jacobian matrix of the affine approximation of the projection transformation.
Rendering by Pixel: Before diving into the final version of 3D GS, we first detail its simpler form to gain a deeper understanding of how it works. 3D GS utilizes multiple technologies to facilitate parallel computing. Given the position of a pixel Alpha synthesis is then employed to calculate the final color for that pixel:
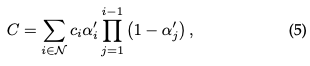
where is the learned color and the final opacity is the product of the learned opacity and the Gaussian value:
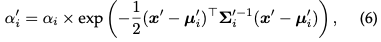
where x′ and μ are coordinates in the projection space. Considering that generating the required sorted lists is difficult to parallelize, the described rendering process may be slower compared to NeRF, which is a legitimate concern. In fact, this concern is valid; rendering speed can be significantly affected when using this simple pixel-by-pixel approach. In order to achieve real-time rendering, 3DGS made some concessions to accommodate parallel computing.
Tiles (Patches): To avoid the computational cost of deriving Gaussian coefficients for each pixel, 3D GS transfers accuracy from pixel level to patch level detail. Specifically, 3D GS initially divides the image into multiple non-overlapping blocks, called “tiles” in the original paper. Figure 3b provides an illustration of tiles. Each tile consists of 16×16 pixels. 3D GS further determines which tiles intersect these projected Gaussian maps. Assuming that the projected Gaussian may cover multiple tiles, the logical approach consists in copying the Gaussian, assigning each copy the identifier of the relevant tile (i.e., tile ID).
Parallel rendering: After copying, 3D GS combines the individual tile IDs with the depth values obtained from the view transformation of each Gaussian. This produces an unsorted list of bytes, where the high-order bits represent the tile ID and the low-order bits represent the depth. By doing this, the sorted list can be used directly for rendering (i.e. alpha compositing). Figures 3c and 3d provide visual demonstrations of these concepts. It’s worth emphasizing that rendering each tile and pixel occurs independently, making this process ideal for parallel computing. Another benefit is that each tile's pixels have access to common shared memory and maintain a uniform read sequence, allowing alpha compositing to be performed in parallel with greater efficiency. In the official implementation of the original paper, the framework treats the processing of tiles and pixels respectively as similar to blocks and threads in the CUDA programming architecture.
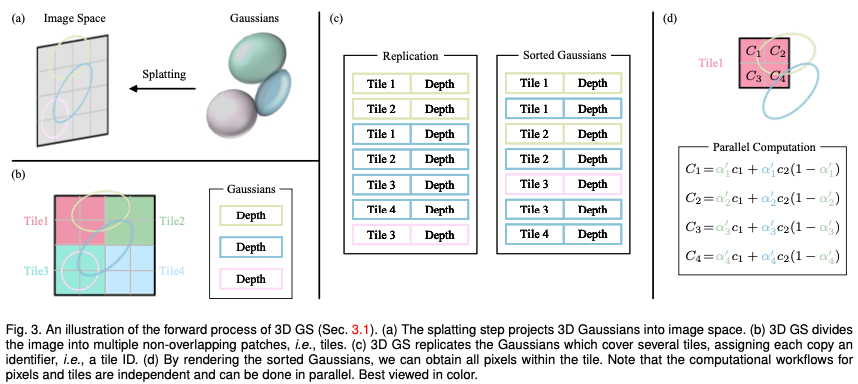
In short, 3D GS introduces several approximations in the forward processing stage to improve computational efficiency while maintaining a high standard of image synthesis quality.
Optimization of 3D Gaussian Splatting
At the core of 3D GS is an optimization process designed to build large collections of 3D Gaussians that accurately capture the essence of the scene, thereby promoting freedom Viewpoint rendering. On the one hand, the properties of 3D Gaussians should be optimized through differentiable rendering to adapt to the texture of a given scene. On the other hand, the number of 3D Gaussians that can represent a given scene well is not known in advance. One promising approach is to have neural networks automatically learn 3D Gaussian densities. We will cover how to optimize the properties of each Gaussian and how to control the density of Gaussians. These two processes are interleaved in the optimization workflow. Since there are many manually set hyperparameters during optimization, we omit the symbols of most hyperparameters for the sake of clarity.
Parameter optimization
Loss function: Once the synthesis of the image is completed, the loss is calculated as the difference between the rendered image and the GT:
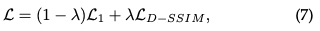
The loss function of 3D-GS is slightly different from that of NeRFs. Due to time-consuming ray-marching, NeRF is usually calculated at the pixel level rather than the image level.
Parameter update: Most characteristics of 3D Gaussian can be optimized directly through backpropagation. It should be noted that directly optimizing the covariance matrix Σ leads to a non-positive semidefinite matrix, which does not comply with the physical interpretation usually associated with the covariance matrix. To avoid this problem, 3D GS chooses to optimize the quaternion q and the 3D vector s. q and s represent rotation and scaling respectively. This approach allows the covariance matrix Σ to be reconstructed as follows:

Density Control
Initialization: 3D GS starts with an initial set of SfM or randomly initialized sparse points. Then, point densification and pruning are used to control the density of the three-dimensional Gaussians.
Point densification: In the point densification stage, 3D GS adaptively increases the Gaussian density to better capture the details of the scene. This process pays particular attention to areas where geometric features are missing or where the Gaussian distribution is too scattered. Densification is performed after a certain number of iterations, targeting Gaussians that exhibit large view-space position gradients (i.e., above a certain threshold). It involves cloning a small Gaussian in under-reconstructed areas, or splitting a large Gaussian in over-reconstructed areas. For cloning, a copy of the Gaussian is created and moved towards the position gradient. For splitting, two smaller Gaussians replace one larger Gaussian, reducing their size by a specific factor. This step seeks the optimal distribution and representation of Gaussians in 3D space, thereby improving the overall quality of the reconstruction.
Point pruning: The point pruning stage involves removing redundant or less influential Gaussians, which can be regarded as a regularization process to some extent. This step is performed by eliminating almost transparent Gaussians (α below a specified threshold) and Gaussians that are too large in world space or view space. Furthermore, to prevent an unreasonable increase in the density of Gaussians near the input camera, the alpha value of the Gaussians is set close to zero after a certain number of iterations. This allows controlling the necessary increase in density of Gaussians while eliminating excess Gaussians. This process not only helps save computational resources but also ensures that the representation of the scene by the Gaussians in the model remains accurate and efficient.
Application Areas and Tasks
The transformative potential of 3D GS extends far beyond its theoretical and computational advances. This section delves into various pioneering application areas where 3D GS is having a significant impact, such as robotics, scene reconstruction and representation, AI-generated content, autonomous driving, and even other scientific disciplines. The application of 3D GS demonstrates its versatility and revolutionary potential. Here, we outline some of the most notable application areas, providing insight into how 3D GS is forming new frontiers in each area.
SLAM
SLAM is a core computational problem in robotics and autonomous systems. It involves the challenge of a robot or device understanding its position in an unknown environment while mapping the layout of the environment. SLAM is critical in a variety of applications, including self-driving cars, augmented reality, and robot navigation. The core of SLAM is to create a map of the unknown environment and determine the location of the device on the map in real time. Therefore, SLAM poses a huge challenge to computationally intensive scene representation technology and is also a good test bed for 3D GS.
3D GS enters the SLAM field as an innovative scene representation method. Traditional SLAM systems typically use point/surface clouds or voxel meshes to represent the environment. In contrast, 3D GS utilizes anisotropic Gaussians to better represent the environment. This representation provides several benefits: 1) Efficiency: Adaptively control the density of 3D Gaussians to compactly represent spatial data and reduce computational load. 2) Accuracy: Anisotropic Gaussian allows for more detailed and accurate environment modeling, especially suitable for complex or dynamically changing scenes. 3) Adaptability: 3D GS can adapt to various scales and complex environments, making it suitable for different SLAM applications. Several innovative studies have used 3D Gaussian splashing in SLAM, demonstrating the potential and versatility of this paradigm.
Dynamic scene modeling
Dynamic scene modeling refers to the process of capturing and representing the three-dimensional structure and appearance of a scene that changes over time. This involves creating a digital model that accurately reflects the geometry, motion and visual aspects of the objects in the scene. Dynamic scene modeling is critical in a variety of applications, including virtual and augmented reality, 3D animation, and computer vision. 4D Gaussian Scattering (4D GS) extends the concept of 3D GS to dynamic scenes. It incorporates the temporal dimension, allowing the representation and rendering of scenes that change over time. This paradigm provides significant improvements in rendering dynamic scenes in real-time while maintaining high-quality visual output.
AIGC
AIGC refers to digital content autonomously created or significantly altered by artificial intelligence systems, particularly in the fields of computer vision, natural language processing, and machine learning. AIGC is characterized by its ability to simulate, extend or enhance artificially generated content, enabling applications ranging from photorealistic image synthesis to dynamic narrative creation. The significance of AIGC lies in its transformative potential in various fields, including entertainment, education and technological development. It is a key element in the evolving digital content creation landscape, providing a scalable, customizable and often more efficient alternative to traditional methods.
This unambiguous feature of 3D GS facilitates real-time rendering capabilities and an unprecedented level of control and editing, making it highly relevant for AIGC applications. 3D GS's explicit scene representation and differentiable rendering algorithm fully meet AIGC's requirements for generating high-fidelity, real-time and editable content, which is crucial for applications in virtual reality, interactive media and other fields.
Autonomous Driving
Autonomous driving is designed to allow vehicles to navigate and operate without human intervention. These vehicles are equipped with a suite of sensors, including cameras, LiDAR and radar, combined with advanced algorithms, machine learning models and powerful computing power. The central goal is to sense the environment, make informed decisions, and execute maneuvers safely and efficiently. Autonomous driving has the potential to transform transportation, providing key benefits such as improving road safety by reducing human error, enhancing mobility for those unable to drive, and optimizing traffic flow, thereby reducing congestion and environmental impact.
Self-driving cars need to sense and interpret their surrounding environment in order to drive safely. This includes reconstructing driving scenes in real time, accurately identifying static and dynamic objects, and understanding their spatial relationships and motion. In dynamic driving scenarios, the environment is constantly changing due to moving objects such as other vehicles, pedestrians or animals. Accurately reconstructing these scenes in real time is critical for safe navigation, but is a challenge due to the complexity and variability of the elements involved. In autonomous driving, 3D GS can be used to reconstruct scenes by blending data points, such as those obtained from sensors such as LiDAR, into a cohesive and continuous representation. This is particularly useful for handling different densities of data points and ensuring smooth and accurate reconstruction of static backgrounds and dynamic objects in a scene. So far, there are few works that use 3D Gaussian to model dynamic driving/street scenes and show excellent performance in scene reconstruction compared with existing methods.
Performance Comparison
This section provides more empirical evidence by showing the performance of several 3D GS algorithms we discussed previously. The diverse applications of 3D GS in many tasks, coupled with the customized algorithm design for each task, make a uniform comparison of all 3D GS algorithms within a single task or dataset impractical. Therefore, we select three representative tasks in the 3D GS field for in-depth performance evaluation. Performances are derived primarily from the original papers unless otherwise stated.
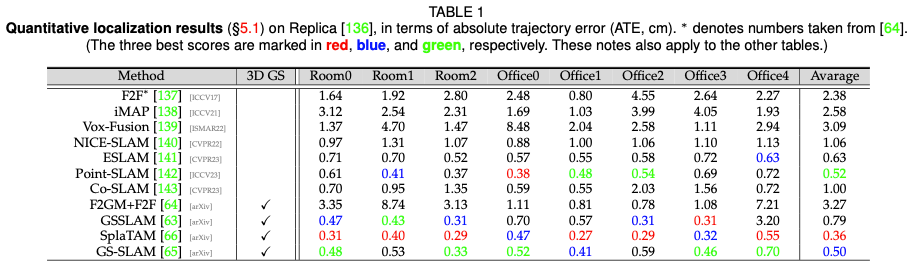
Positioning performance
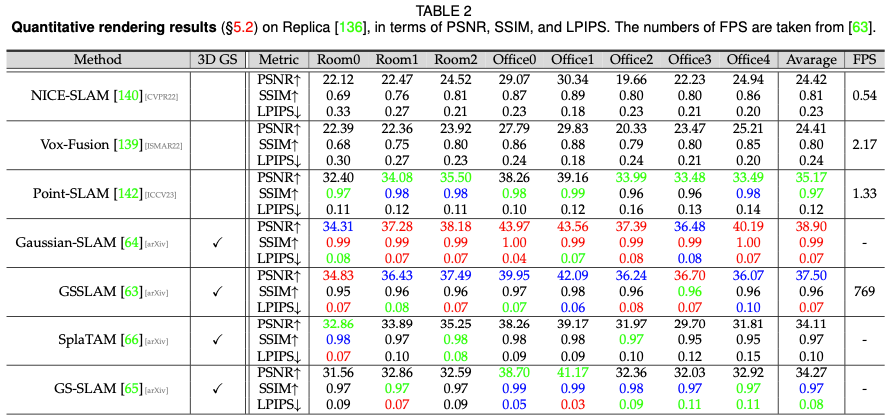
Static scene rendering performance
Dynamic scene rendering performance
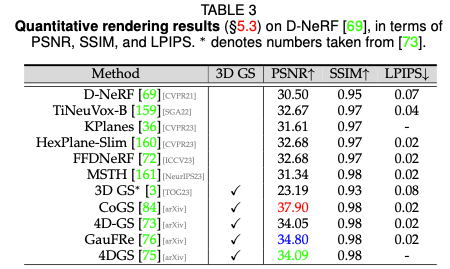
Driving scene rendering performance
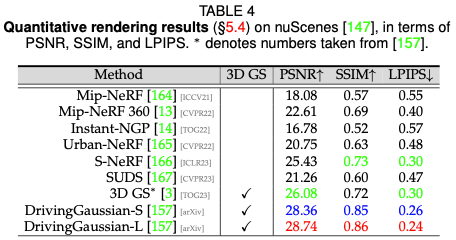
Digital Human Performance
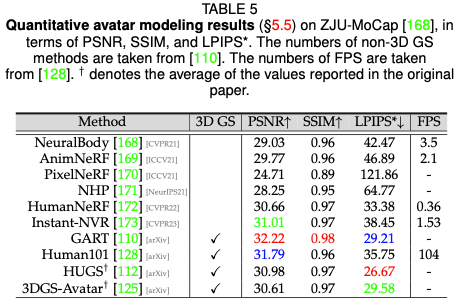
Future Research Direction
Although 3D The follow-up work on GS has made significant progress, but we believe there are still some challenges that need to be overcome.
- Data Efficient 3D GS Solutions: Generating novel views and reconstructing scenes from limited data points is of great interest, especially since they have the potential to enhance realism and user experience with minimal input . Recent advances have explored the use of depth information, dense probability distributions, and pixel-to-Gaussian mapping to facilitate this capability. However, further exploration in this area is still urgently needed. In addition, a significant problem of 3D GS is the occurrence of artifacts in areas with insufficient observational data. This challenge is a common limitation in radiation field rendering, as sparse data often leads to inaccurate reconstructions. Therefore, developing new data interpolation or integration methods in these sparse regions represents a promising avenue for future research.
- Memory-efficient 3D GS solution: While 3D GS demonstrates extraordinary capabilities, its scalability poses significant challenges, especially when collocated with NeRF-based methods. The latter benefits from the simplicity of storing only the parameters of the learned MLP. This scalability problem becomes increasingly severe in the context of large-scale scene management, where computational and memory requirements increase significantly. Therefore, there is an urgent need to optimize memory utilization during the training phase and model storage. Exploring more efficient data structures and investigating advanced compression techniques are promising avenues to address these limitations.
- Advanced rendering algorithm: The current rendering pipeline of 3D GS is forward and can be further optimized. For example, a simple visibility algorithm can cause drastic switching of Gaussian depth/blending order. This highlights an important opportunity for future research: implementing more advanced rendering algorithms. These improved methods should aim to more accurately simulate the complex interactions of light and material properties in a given scene. A promising approach might involve assimilating and adapting established principles from traditional computer graphics to the specific context of 3D GS. Notable in this regard are the ongoing efforts to integrate enhanced rendering techniques or hybrid models into the current computational framework of 3D GS. In addition, the exploration of inverse rendering and its applications provides fertile ground for research.
- Optimization and regularization: Although anisotropic Gaussian is good for representing complex geometric shapes, it can produce visual artifacts. For example, those large 3D Gaussians, especially in areas with view-dependent appearance, can cause pop-in artifacts, where visual elements suddenly appear or disappear, breaking immersion. There is considerable exploration potential in regularization and optimization of 3D GS. Introducing anti-aliasing can mitigate sudden changes in Gaussian depth and blending order. Enhancements to the optimization algorithm may provide better control over the Gaussian coefficients in space. Additionally, incorporating regularization into the optimization process can speed up convergence, smooth visual noise, or improve image quality. Furthermore, such a large number of hyperparameters affects the generalization of 3D GS, which urgently needs solutions.
- 3D Gaussians in Mesh Reconstruction: The potential of 3D GS in mesh reconstruction and its place in the spectrum of volume and surface representations have yet to be fully explored. There is an urgent need to study how Gaussian primitives are suitable for mesh reconstruction tasks. This exploration could bridge the gap between volumetric rendering and traditional surface-based methods, providing insights into new rendering techniques and applications.
- Empowering 3D GS with more possibilities: Despite the huge potential of 3D GS, the full range of applications of 3D GS remains largely unexplored. One promising avenue to explore is to enhance 3D Gaussians with additional properties, such as linguistic and physical properties tailored for specific applications. Furthermore, recent research has begun to reveal the capabilities of 3D GS in several areas, such as camera pose estimation, capture of hand-object interactions, and quantification of uncertainty. These preliminary findings provide important opportunities for interdisciplinary scholars to further explore 3D GS.
Conclusion
To our knowledge, this review provides the first comprehensive overview of 3D GS, a revolutionary explicit radiation field and computer Graphics technology. It depicts a paradigm shift from traditional NeRF methods, highlighting the advantages of 3D GS in real-time rendering and enhanced controllability. Our detailed analysis demonstrates the advantages of 3D GS in real-world applications, especially those requiring real-time performance. We provide insights into future research directions and unsolved challenges in the field. Overall, 3D GS is a transformative technology that is expected to have a significant impact on the future development of 3D reconstruction and representation. This survey is intended to serve as a foundational resource to drive further exploration and progress in this rapidly developing field.

Original link: https://mp.weixin.qq.com/s/jH4g4Cx87nPUYN8iKaKcBA
The above is the detailed content of Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?
Jan 17, 2024 pm 02:57 PM
Why is Gaussian Splatting so popular in autonomous driving that NeRF is starting to be abandoned?
Jan 17, 2024 pm 02:57 PM
Written above & the author’s personal understanding Three-dimensional Gaussiansplatting (3DGS) is a transformative technology that has emerged in the fields of explicit radiation fields and computer graphics in recent years. This innovative method is characterized by the use of millions of 3D Gaussians, which is very different from the neural radiation field (NeRF) method, which mainly uses an implicit coordinate-based model to map spatial coordinates to pixel values. With its explicit scene representation and differentiable rendering algorithms, 3DGS not only guarantees real-time rendering capabilities, but also introduces an unprecedented level of control and scene editing. This positions 3DGS as a potential game-changer for next-generation 3D reconstruction and representation. To this end, we provide a systematic overview of the latest developments and concerns in the field of 3DGS for the first time.
 How to solve the long tail problem in autonomous driving scenarios?
Jun 02, 2024 pm 02:44 PM
How to solve the long tail problem in autonomous driving scenarios?
Jun 02, 2024 pm 02:44 PM
Yesterday during the interview, I was asked whether I had done any long-tail related questions, so I thought I would give a brief summary. The long-tail problem of autonomous driving refers to edge cases in autonomous vehicles, that is, possible scenarios with a low probability of occurrence. The perceived long-tail problem is one of the main reasons currently limiting the operational design domain of single-vehicle intelligent autonomous vehicles. The underlying architecture and most technical issues of autonomous driving have been solved, and the remaining 5% of long-tail problems have gradually become the key to restricting the development of autonomous driving. These problems include a variety of fragmented scenarios, extreme situations, and unpredictable human behavior. The "long tail" of edge scenarios in autonomous driving refers to edge cases in autonomous vehicles (AVs). Edge cases are possible scenarios with a low probability of occurrence. these rare events
 Choose camera or lidar? A recent review on achieving robust 3D object detection
Jan 26, 2024 am 11:18 AM
Choose camera or lidar? A recent review on achieving robust 3D object detection
Jan 26, 2024 am 11:18 AM
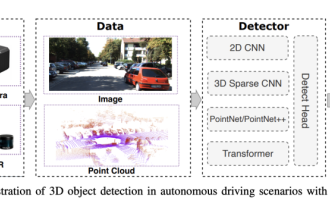
0.Written in front&& Personal understanding that autonomous driving systems rely on advanced perception, decision-making and control technologies, by using various sensors (such as cameras, lidar, radar, etc.) to perceive the surrounding environment, and using algorithms and models for real-time analysis and decision-making. This enables vehicles to recognize road signs, detect and track other vehicles, predict pedestrian behavior, etc., thereby safely operating and adapting to complex traffic environments. This technology is currently attracting widespread attention and is considered an important development area in the future of transportation. one. But what makes autonomous driving difficult is figuring out how to make the car understand what's going on around it. This requires that the three-dimensional object detection algorithm in the autonomous driving system can accurately perceive and describe objects in the surrounding environment, including their locations,
 CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
CLIP-BEVFormer: Explicitly supervise the BEVFormer structure to improve long-tail detection performance
Mar 26, 2024 pm 12:41 PM
Written above & the author’s personal understanding: At present, in the entire autonomous driving system, the perception module plays a vital role. The autonomous vehicle driving on the road can only obtain accurate perception results through the perception module. The downstream regulation and control module in the autonomous driving system makes timely and correct judgments and behavioral decisions. Currently, cars with autonomous driving functions are usually equipped with a variety of data information sensors including surround-view camera sensors, lidar sensors, and millimeter-wave radar sensors to collect information in different modalities to achieve accurate perception tasks. The BEV perception algorithm based on pure vision is favored by the industry because of its low hardware cost and easy deployment, and its output results can be easily applied to various downstream tasks.
 This article is enough for you to read about autonomous driving and trajectory prediction!
Feb 28, 2024 pm 07:20 PM
This article is enough for you to read about autonomous driving and trajectory prediction!
Feb 28, 2024 pm 07:20 PM
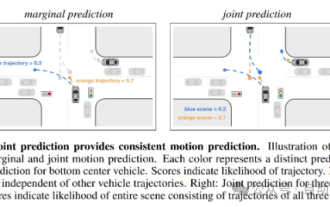
Trajectory prediction plays an important role in autonomous driving. Autonomous driving trajectory prediction refers to predicting the future driving trajectory of the vehicle by analyzing various data during the vehicle's driving process. As the core module of autonomous driving, the quality of trajectory prediction is crucial to downstream planning control. The trajectory prediction task has a rich technology stack and requires familiarity with autonomous driving dynamic/static perception, high-precision maps, lane lines, neural network architecture (CNN&GNN&Transformer) skills, etc. It is very difficult to get started! Many fans hope to get started with trajectory prediction as soon as possible and avoid pitfalls. Today I will take stock of some common problems and introductory learning methods for trajectory prediction! Introductory related knowledge 1. Are the preview papers in order? A: Look at the survey first, p
 Let's talk about end-to-end and next-generation autonomous driving systems, as well as some misunderstandings about end-to-end autonomous driving?
Apr 15, 2024 pm 04:13 PM
Let's talk about end-to-end and next-generation autonomous driving systems, as well as some misunderstandings about end-to-end autonomous driving?
Apr 15, 2024 pm 04:13 PM
In the past month, due to some well-known reasons, I have had very intensive exchanges with various teachers and classmates in the industry. An inevitable topic in the exchange is naturally end-to-end and the popular Tesla FSDV12. I would like to take this opportunity to sort out some of my thoughts and opinions at this moment for your reference and discussion. How to define an end-to-end autonomous driving system, and what problems should be expected to be solved end-to-end? According to the most traditional definition, an end-to-end system refers to a system that inputs raw information from sensors and directly outputs variables of concern to the task. For example, in image recognition, CNN can be called end-to-end compared to the traditional feature extractor + classifier method. In autonomous driving tasks, input data from various sensors (camera/LiDAR
 SIMPL: A simple and efficient multi-agent motion prediction benchmark for autonomous driving
Feb 20, 2024 am 11:48 AM
SIMPL: A simple and efficient multi-agent motion prediction benchmark for autonomous driving
Feb 20, 2024 am 11:48 AM
Original title: SIMPL: ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Paper link: https://arxiv.org/pdf/2402.02519.pdf Code link: https://github.com/HKUST-Aerial-Robotics/SIMPL Author unit: Hong Kong University of Science and Technology DJI Paper idea: This paper proposes a simple and efficient motion prediction baseline (SIMPL) for autonomous vehicles. Compared with traditional agent-cent
 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
Target detection is a relatively mature problem in autonomous driving systems, among which pedestrian detection is one of the earliest algorithms to be deployed. Very comprehensive research has been carried out in most papers. However, distance perception using fisheye cameras for surround view is relatively less studied. Due to large radial distortion, standard bounding box representation is difficult to implement in fisheye cameras. To alleviate the above description, we explore extended bounding box, ellipse, and general polygon designs into polar/angular representations and define an instance segmentation mIOU metric to analyze these representations. The proposed model fisheyeDetNet with polygonal shape outperforms other models and simultaneously achieves 49.5% mAP on the Valeo fisheye camera dataset for autonomous driving





