 Technology peripherals
Technology peripherals
 AI
AI
 Google Mathematical AI publishes an article in Nature: Proving beyond Wu Wenjun's 1978 law theorem, demonstrating world-class geometric level
Google Mathematical AI publishes an article in Nature: Proving beyond Wu Wenjun's 1978 law theorem, demonstrating world-class geometric level
Google Mathematical AI publishes an article in Nature: Proving beyond Wu Wenjun's 1978 law theorem, demonstrating world-class geometric level
Google DeepMind releases Nature again, the Alpha series of AI returns, and the level of mathematics improves by leaps and bounds.
AlphaGeometry, no need for human demonstration to reach the geometric level of IMO gold medal players.

It feels like AlphaZero learned the game "Mastering the game of Go without human knowledge" back then.
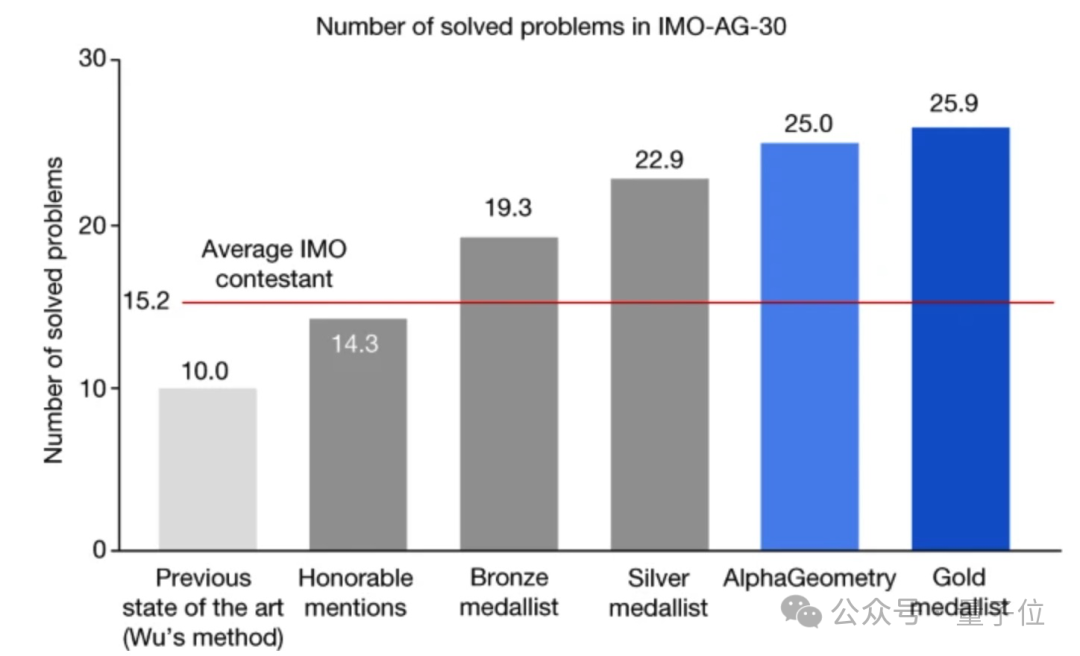
AlphaGeometry got 25 of the 30 IMO difficulty geometric theorem proving questions right, while the average human gold medal player got 25.9 right. In addition, the previous SOTA method (Wu Wenjun method in 1978) could only get 10 correct.
IMO gold medalist陈伊婷(Evan Chen) is responsible for evaluating the answers generated by the AI. He commented:
AlphaGeometry's output is impressive, both reliable and clean. Past AI solutions have been hit-and-miss, resulting in output that sometimes required manual review.
AlphaGeometry's solutions have a verifiable structure that can be verified by both machines and understood by humans. It uses classic geometry rules like angles and similar triangles just like students.
In addition to the outstanding results, there are three key points in this study that have attracted the attention of the industry:
- No need for human demonstration, that is, only AI synthetic data training is used, continuing AlphaZero’s self-learning Go method.
- Large model combined with other AI methods, similar to AlphaGo and OpenAI Q* rumors.
- Unlike many previous methods, AlphaGeometry can generate human-readable proofs, and both the model and code are open source.
#The team believes that AlphaGeometry provides a potential framework for achieving advanced reasoning capabilities and discovering new knowledge.
This may help advance theorem proving in artificial intelligence - seen as a key step in building AGI.

In addition, during the communication process with the author's team, Qubits inquired whether AlphaGeometry would really be allowed to participate in an IMO competition, just like the AlphaGo challenge back then. Like the human Go champion.
They said they are working hard to improve the system's capabilities and also need to enable AI to solve a wider range of mathematical problems beyond geometry.
AI proves that geometry also draws auxiliary lines
Previously, the AI system could not solve geometric problems well, and it was stuck due to the lack of high-quality training data.
Humans learning geometry can use paper and pen to use existing knowledge on images to discover new and more complex geometric properties and relationships.
The Google team generated 1 billion random geometric object graphs for this purpose, as well as all the relationships between their points and lines, and finally screened out 100 million unique theorems and proofs of different difficulties. AlphaGeometry completely performed on these data Train from scratch.

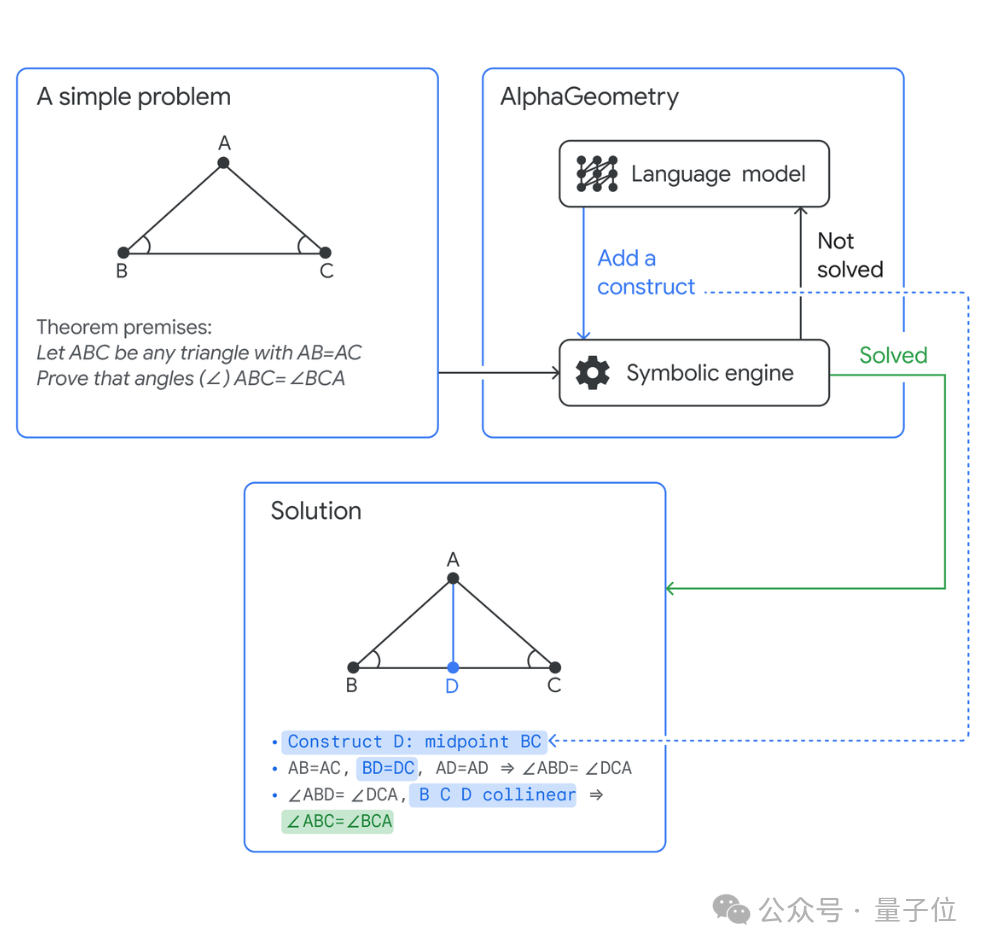
The system consists of two modules that cooperate with each other to find complex geometric proofs.
- Language model, predicts the geometric structure that can be used to solve the problem (that is, adding auxiliary lines) .
- Symbolic reasoning engine, uses logical rules to derive conclusions.
First author Trieu Trinh introduced that the operation process of AlphaGeometry is similar to that the human brain is divided into two types: fast and slow.
This is the concept of "System 1, System 2" popularized in the best-selling book "Thinking Fast and Slow" by Nobel Prize winner Daniel Kahneman.
System 1 provides quick, intuitive ideas, and System 2 provides more thoughtful, rational decisions.
On the one hand, language models are good at identifying patterns and relationships in data and can quickly predict potentially useful auxiliary structures, but often lack the ability to rigorously reason or explain their decisions.
On the other hand, symbolic reasoning engines are based on formal logic and use explicit rules to draw conclusions. They are rational and explainable, but they are slow and inflexible, especially when dealing with large, complex problems alone.
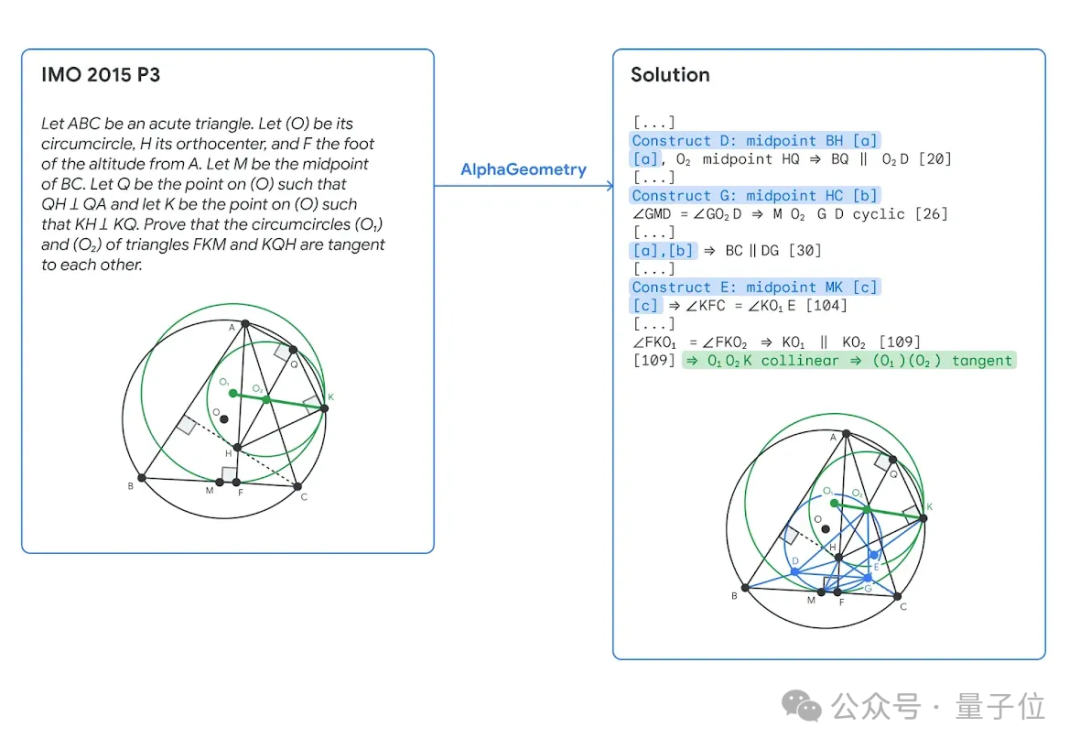
For example, when solving an IMO 2015 competition question, the blue part is the auxiliary structure added by AlphaGeometry's language model, and the green part is the simplified version of the final proof, with a total of 109 steps.
During the process of solving the problem, AlphaGeometry also discovered an unused prerequisite in the 2004 IMO competition question, and thus discovered a broader version of the theorem.
It can be proved that P, B, and C are collinear without the condition that O is the midpoint of BC.
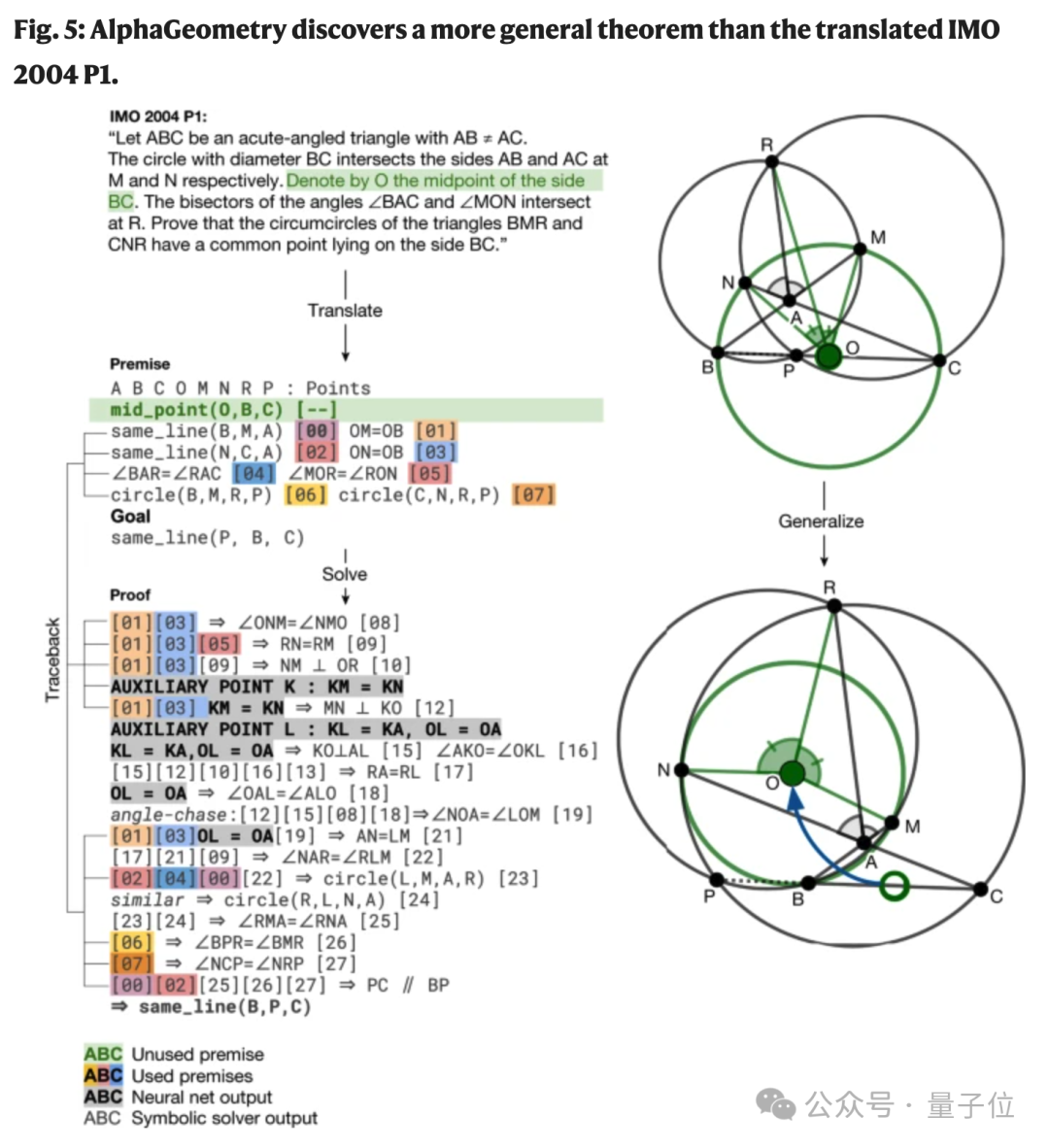
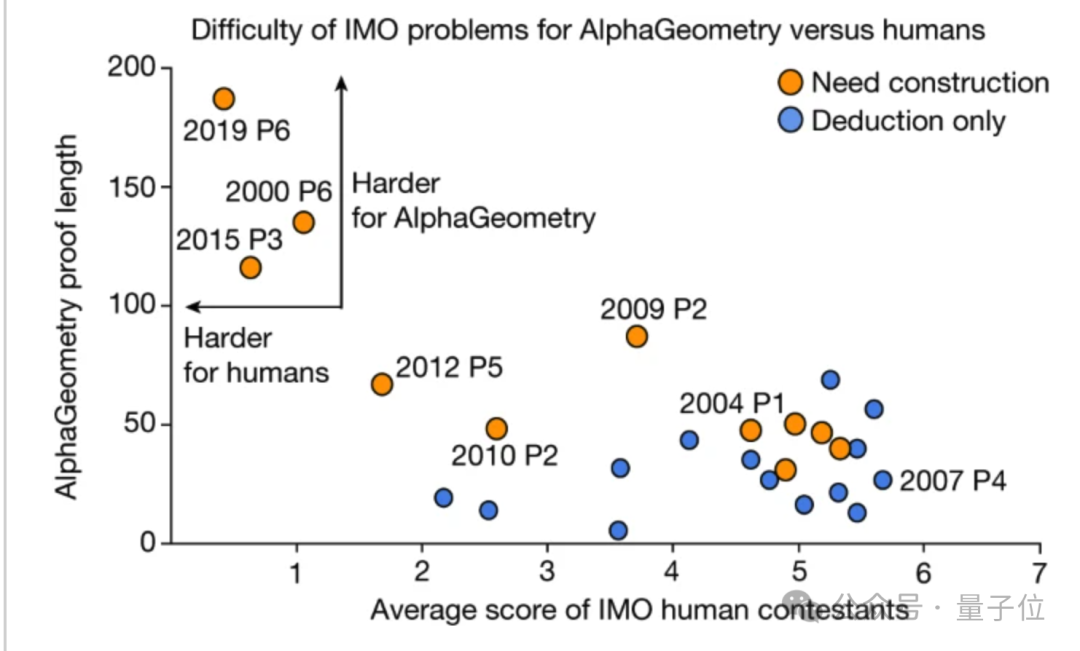
In addition, the study also found that for the three problems with the lowest human scores, AlphaGeometry also requires a very long proving process and the addition of a lot of auxiliary structures to solve.
But on the relatively easy questions, there was no significant correlation between the average human score and the length of the proof generated by the AI (p = −0.06).
One More Thing
Regarding the connection and difference between AlphaGeometry and AlphaGo, during the communication process with the team, Google scientistQuoc Le Introduction:
They all search in a very complex decision space, but AlphaGo’s method is more traditional(Note: Neural network is responsible for pattern recognition), The neural network in AlphaGeometry is responsible for suggesting the next action to be taken and guiding the search algorithm to move in the right direction in the decision space.
Although this result is named after the Alpha series, and the first unit is also Google DeepMind, the author is actually a former Google Brain member.
Quoc Le master needs no introduction. Trieu Trinh, the first author, and Thang Luong, the corresponding author, have both worked at Google for six or seven years. Thang Luong himself was also an IMO player in high school.
Among the two Chinese authors, He He is an assistant professor at New York University. Wu Yuhuai previously participated in the research of Google's large mathematical model Minerva, and has now left Google to join Musk's team and become one of the co-founders of xAI.
Paper address: https://www.nature.com/articles/s41586-023-06747-5.
Reference link:
[1]https://www.nature.com/articles/d4186-024-00141 -5.
[2]https://deepmind.google/discover/blog/alphageometry-an-olympiad-level-ai-system-for-geometry.
The above is the detailed content of Google Mathematical AI publishes an article in Nature: Proving beyond Wu Wenjun's 1978 law theorem, demonstrating world-class geometric level. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How to comment deepseek
Feb 19, 2025 pm 05:42 PM
How to comment deepseek
Feb 19, 2025 pm 05:42 PM
DeepSeek is a powerful information retrieval tool. Its advantage is that it can deeply mine information, but its disadvantages are that it is slow, the result presentation method is simple, and the database coverage is limited. It needs to be weighed according to specific needs.
 How to search deepseek
Feb 19, 2025 pm 05:39 PM
How to search deepseek
Feb 19, 2025 pm 05:39 PM
DeepSeek is a proprietary search engine that only searches in a specific database or system, faster and more accurate. When using it, users are advised to read the document, try different search strategies, seek help and feedback on the user experience in order to make the most of their advantages.
 Sesame Open Door Exchange Web Page Registration Link Gate Trading App Registration Website Latest
Feb 28, 2025 am 11:06 AM
Sesame Open Door Exchange Web Page Registration Link Gate Trading App Registration Website Latest
Feb 28, 2025 am 11:06 AM
This article introduces the registration process of the Sesame Open Exchange (Gate.io) web version and the Gate trading app in detail. Whether it is web registration or app registration, you need to visit the official website or app store to download the genuine app, then fill in the user name, password, email, mobile phone number and other information, and complete email or mobile phone verification.
 Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download Address
Feb 28, 2025 am 10:51 AM
Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download Address
Feb 28, 2025 am 10:51 AM
It is crucial to choose a formal channel to download the app and ensure the safety of your account.
 Why can't the Bybit exchange link be directly downloaded and installed?
Feb 21, 2025 pm 10:57 PM
Why can't the Bybit exchange link be directly downloaded and installed?
Feb 21, 2025 pm 10:57 PM
Why can’t the Bybit exchange link be directly downloaded and installed? Bybit is a cryptocurrency exchange that provides trading services to users. The exchange's mobile apps cannot be downloaded directly through AppStore or GooglePlay for the following reasons: 1. App Store policy restricts Apple and Google from having strict requirements on the types of applications allowed in the app store. Cryptocurrency exchange applications often do not meet these requirements because they involve financial services and require specific regulations and security standards. 2. Laws and regulations Compliance In many countries, activities related to cryptocurrency transactions are regulated or restricted. To comply with these regulations, Bybit Application can only be used through official websites or other authorized channels
 gate.io exchange official registration portal
Feb 20, 2025 pm 04:27 PM
gate.io exchange official registration portal
Feb 20, 2025 pm 04:27 PM
Gate.io is a leading cryptocurrency exchange that offers a wide range of crypto assets and trading pairs. Registering Gate.io is very simple. You just need to visit its official website or download the app, click "Register", fill in the registration form, verify your email, and set up two-factor verification (2FA), and you can complete the registration. With Gate.io, users can enjoy a safe and convenient cryptocurrency trading experience.
 Binance binance official website latest version login portal
Feb 21, 2025 pm 05:42 PM
Binance binance official website latest version login portal
Feb 21, 2025 pm 05:42 PM
To access the latest version of Binance website login portal, just follow these simple steps. Go to the official website and click the "Login" button in the upper right corner. Select your existing login method. If you are a new user, please "Register". Enter your registered mobile number or email and password and complete authentication (such as mobile verification code or Google Authenticator). After successful verification, you can access the latest version of Binance official website login portal.
 The latest download address of Bitget in 2025: Steps to obtain the official app
Feb 25, 2025 pm 02:54 PM
The latest download address of Bitget in 2025: Steps to obtain the official app
Feb 25, 2025 pm 02:54 PM
This guide provides detailed download and installation steps for the official Bitget Exchange app, suitable for Android and iOS systems. The guide integrates information from multiple authoritative sources, including the official website, the App Store, and Google Play, and emphasizes considerations during download and account management. Users can download the app from official channels, including app store, official website APK download and official website jump, and complete registration, identity verification and security settings. In addition, the guide covers frequently asked questions and considerations, such as





