Definition and application of OLS regression

Ordinary Least Squares (OLS) regression is an optimization strategy designed to find the closest straight line to the data points in a linear regression model. OLS is widely regarded as the most effective optimization method in linear regression models because of its ability to provide unbiased estimates of alpha and beta. By minimizing the sum of squares of the residuals, OLS can find the optimal parameter values so that the regression line has the highest fitting degree to the data points. This method not only helps us understand the relationship between independent variables and dependent variables, but also allows for predictive and inferential analysis. Overall, OLS regression is a simple yet powerful tool that can help us explain and predict
How OLS is applied to linear regression
Linear regression is a method used in supervised machine learning Algorithm for the task. It is mainly applied to regression problems, not classification problems. Regression problems involve predicting continuous values, while classification problems predict categories. Therefore, the goal of the linear regression algorithm is to predict a continuous target variable by building a linear model. Unlike classification, the target variable is not a categorical value, but a numerical or continuous value. Through the linear regression algorithm, we can predict a continuous number based on the linear relationship of the input variables to model and predict the problem.
Regression tasks can be divided into two categories: one is a task that uses only one feature to predict the target, and the other is a task that uses multiple features to predict the target.
How to find OLS in a linear regression model
The goal of simple linear regression is to minimize the error term by adjusting the parameters. Specifically, the model adopts the minimization of the squared error as the optimization objective. We don't want positive and negative errors to cancel each other out, as they will both penalize our model. Therefore, this process is called ordinary least squares (OLS) error.
In summary, OLS is an optimization strategy used to fit straight lines of data points. Although OLS is not the only optimization strategy, it is one of the most popular because it provides unbiased estimators of the actual values of alpha and beta.
According to the Gauss-Markov theorem and the assumptions of the linear regression model, the OLS estimator is based on the linearity of the parameters, random sampling of observations, zero conditional mean, no multicollinearity and error homoskedasticity. is considered to be the best unbiased linear estimator.
The above is the detailed content of Definition and application of OLS regression. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1386
1386
 52
52
 Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
This site reported on June 27 that Jianying is a video editing software developed by FaceMeng Technology, a subsidiary of ByteDance. It relies on the Douyin platform and basically produces short video content for users of the platform. It is compatible with iOS, Android, and Windows. , MacOS and other operating systems. Jianying officially announced the upgrade of its membership system and launched a new SVIP, which includes a variety of AI black technologies, such as intelligent translation, intelligent highlighting, intelligent packaging, digital human synthesis, etc. In terms of price, the monthly fee for clipping SVIP is 79 yuan, the annual fee is 599 yuan (note on this site: equivalent to 49.9 yuan per month), the continuous monthly subscription is 59 yuan per month, and the continuous annual subscription is 499 yuan per year (equivalent to 41.6 yuan per month) . In addition, the cut official also stated that in order to improve the user experience, those who have subscribed to the original VIP
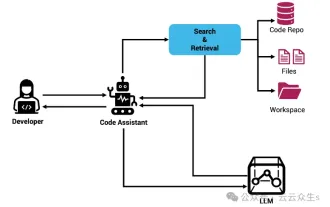 Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Improve developer productivity, efficiency, and accuracy by incorporating retrieval-enhanced generation and semantic memory into AI coding assistants. Translated from EnhancingAICodingAssistantswithContextUsingRAGandSEM-RAG, author JanakiramMSV. While basic AI programming assistants are naturally helpful, they often fail to provide the most relevant and correct code suggestions because they rely on a general understanding of the software language and the most common patterns of writing software. The code generated by these coding assistants is suitable for solving the problems they are responsible for solving, but often does not conform to the coding standards, conventions and styles of the individual teams. This often results in suggestions that need to be modified or refined in order for the code to be accepted into the application
 Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Large Language Models (LLMs) are trained on huge text databases, where they acquire large amounts of real-world knowledge. This knowledge is embedded into their parameters and can then be used when needed. The knowledge of these models is "reified" at the end of training. At the end of pre-training, the model actually stops learning. Align or fine-tune the model to learn how to leverage this knowledge and respond more naturally to user questions. But sometimes model knowledge is not enough, and although the model can access external content through RAG, it is considered beneficial to adapt the model to new domains through fine-tuning. This fine-tuning is performed using input from human annotators or other LLM creations, where the model encounters additional real-world knowledge and integrates it
 Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
To learn more about AIGC, please visit: 51CTOAI.x Community https://www.51cto.com/aigc/Translator|Jingyan Reviewer|Chonglou is different from the traditional question bank that can be seen everywhere on the Internet. These questions It requires thinking outside the box. Large Language Models (LLMs) are increasingly important in the fields of data science, generative artificial intelligence (GenAI), and artificial intelligence. These complex algorithms enhance human skills and drive efficiency and innovation in many industries, becoming the key for companies to remain competitive. LLM has a wide range of applications. It can be used in fields such as natural language processing, text generation, speech recognition and recommendation systems. By learning from large amounts of data, LLM is able to generate text
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A
 SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
Editor | KX In the field of drug research and development, accurately and effectively predicting the binding affinity of proteins and ligands is crucial for drug screening and optimization. However, current studies do not take into account the important role of molecular surface information in protein-ligand interactions. Based on this, researchers from Xiamen University proposed a novel multi-modal feature extraction (MFE) framework, which for the first time combines information on protein surface, 3D structure and sequence, and uses a cross-attention mechanism to compare different modalities. feature alignment. Experimental results demonstrate that this method achieves state-of-the-art performance in predicting protein-ligand binding affinities. Furthermore, ablation studies demonstrate the effectiveness and necessity of protein surface information and multimodal feature alignment within this framework. Related research begins with "S
 SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
According to news from this site on August 1, SK Hynix released a blog post today (August 1), announcing that it will attend the Global Semiconductor Memory Summit FMS2024 to be held in Santa Clara, California, USA from August 6 to 8, showcasing many new technologies. generation product. Introduction to the Future Memory and Storage Summit (FutureMemoryandStorage), formerly the Flash Memory Summit (FlashMemorySummit) mainly for NAND suppliers, in the context of increasing attention to artificial intelligence technology, this year was renamed the Future Memory and Storage Summit (FutureMemoryandStorage) to invite DRAM and storage vendors and many more players. New product SK hynix launched last year




