Reinforcement learning policy gradient algorithm

The policy gradient algorithm is an important reinforcement learning algorithm. Its core idea is to search for the best strategy by directly optimizing the policy function. Compared with the method of indirectly optimizing the value function, the policy gradient algorithm has better convergence and stability, and can handle continuous action space problems, so it is widely used. The advantage of this algorithm is that it can directly learn the policy parameters without the need for an estimated value function. This enables the policy gradient algorithm to cope with the complex problems of high-dimensional state space and continuous action space. In addition, the policy gradient algorithm can also approximate the gradient through sampling, thereby improving computational efficiency. In short, the policy gradient algorithm is a powerful and flexible method. In the policy gradient algorithm, we need to define a policy function\pi(a|s), which gives The probability of taking action a in state s. Our goal is to optimize this policy function so that it produces the maximum expected reward in the sense of long-term cumulative reward. Specifically, we need to maximize the expected return J(\theta) of the policy function:
J(\theta)=\mathbb{E}_{\tau\sim p_\ theta(\tau)}[R(\tau)]
Among them, \theta is the parameter of the strategy function, \tau represents a trajectory, and p_\theta(\tau) is the strategy The function generates the probability distribution of trajectory \tau, and R(\tau) is the return of trajectory \tau.
In order to maximize the expected return J(\theta), we need to optimize the policy function and use the gradient ascent algorithm. Specifically, we need to calculate the gradient of the policy function\nabla_\theta J(\theta), and then update the parameters of the policy function\theta according to the direction of the gradient. The gradient of the policy function can be calculated using importance sampling and logarithmic gradient techniques.
\nabla_\theta J(\theta)=\mathbb{E}_{\tau\sim p_\theta(\tau)}[\sum_{t=0}^ {T-1}\nabla_\theta\log\pi(a_t|s_t)R(\tau)]
Where, T is the length of the trajectory, \log\pi(a_t |s_t) is the logarithm of the policy function, which represents the logarithm of the probability of taking action a_t in state s_t, and R(\tau) is the reward of the trajectory.
The policy gradient algorithm can use different optimization methods to update the parameters of the policy function. Among them, gradient-based optimization method is a commonly used method. Specifically, we can use the stochastic gradient ascent algorithm (SGA) to update the parameters of the policy function, the formula is as follows:
\theta_{t 1}=\theta_t \alpha\nabla_\ theta\hat{J}(\theta_t)
where \alpha is the learning rate, \hat{J}(\theta_t) is the expectation estimated using the average return of a batch of trajectories Return J(\theta_t). In practical applications, we can use neural networks to represent the policy function, then use the backpropagation algorithm to calculate the gradient of the policy function, and use the optimizer to update the parameters of the policy function.
The policy gradient algorithm has many variants, such as the baseline policy gradient algorithm, Actor-Critic algorithm, TRPO algorithm and PPO algorithm, etc. These algorithms all use different techniques to improve the performance and stability of the policy gradient algorithm. For example, the baseline policy gradient algorithm reduces variance by introducing a baseline function, the Actor-Critic algorithm improves efficiency by introducing a value function, the TRPO algorithm ensures convergence by limiting the update amplitude of the policy function, and the PPO algorithm uses techniques such as shearing and cropping To balance the update of the policy function and ensure stability.
The policy gradient algorithm is widely used in practice and has been successfully used in many fields, such as robot control, game playing, natural language processing, etc. It has many advantages, such as the ability to handle continuous action space problems, better convergence and stability, etc. However, the policy gradient algorithm also has some problems, such as slow convergence and vulnerability to local optimal solutions. Therefore, future research needs to further improve the policy gradient algorithm to improve its performance and application range.
The above is the detailed content of Reinforcement learning policy gradient algorithm. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1376
1376
 52
52
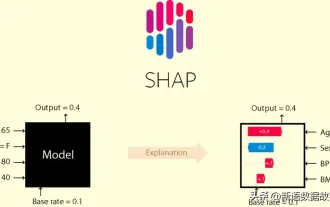 This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
In the fields of machine learning and data science, model interpretability has always been a focus of researchers and practitioners. With the widespread application of complex models such as deep learning and ensemble methods, understanding the model's decision-making process has become particularly important. Explainable AI|XAI helps build trust and confidence in machine learning models by increasing the transparency of the model. Improving model transparency can be achieved through methods such as the widespread use of multiple complex models, as well as the decision-making processes used to explain the models. These methods include feature importance analysis, model prediction interval estimation, local interpretability algorithms, etc. Feature importance analysis can explain the decision-making process of a model by evaluating the degree of influence of the model on the input features. Model prediction interval estimate
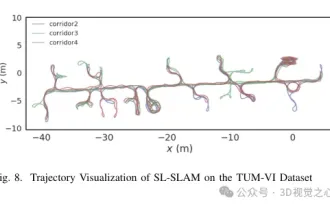 Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Written previously, today we discuss how deep learning technology can improve the performance of vision-based SLAM (simultaneous localization and mapping) in complex environments. By combining deep feature extraction and depth matching methods, here we introduce a versatile hybrid visual SLAM system designed to improve adaptation in challenging scenarios such as low-light conditions, dynamic lighting, weakly textured areas, and severe jitter. sex. Our system supports multiple modes, including extended monocular, stereo, monocular-inertial, and stereo-inertial configurations. In addition, it also analyzes how to combine visual SLAM with deep learning methods to inspire other research. Through extensive experiments on public datasets and self-sampled data, we demonstrate the superiority of SL-SLAM in terms of positioning accuracy and tracking robustness.
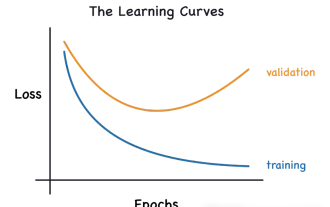 Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves. Underfitting and overfitting 1. Overfitting If a model is overtrained on the data so that it learns noise from it, then the model is said to be overfitting. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score. Slightly modified: "Cause of overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set as a training set may not represent the correct representation of all data." 2. Underfitting Heru
 The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
In the 1950s, artificial intelligence (AI) was born. That's when researchers discovered that machines could perform human-like tasks, such as thinking. Later, in the 1960s, the U.S. Department of Defense funded artificial intelligence and established laboratories for further development. Researchers are finding applications for artificial intelligence in many areas, such as space exploration and survival in extreme environments. Space exploration is the study of the universe, which covers the entire universe beyond the earth. Space is classified as an extreme environment because its conditions are different from those on Earth. To survive in space, many factors must be considered and precautions must be taken. Scientists and researchers believe that exploring space and understanding the current state of everything can help understand how the universe works and prepare for potential environmental crises
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Translator | Reviewed by Li Rui | Chonglou Artificial intelligence (AI) and machine learning (ML) models are becoming increasingly complex today, and the output produced by these models is a black box – unable to be explained to stakeholders. Explainable AI (XAI) aims to solve this problem by enabling stakeholders to understand how these models work, ensuring they understand how these models actually make decisions, and ensuring transparency in AI systems, Trust and accountability to address this issue. This article explores various explainable artificial intelligence (XAI) techniques to illustrate their underlying principles. Several reasons why explainable AI is crucial Trust and transparency: For AI systems to be widely accepted and trusted, users need to understand how decisions are made
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Machine learning is an important branch of artificial intelligence that gives computers the ability to learn from data and improve their capabilities without being explicitly programmed. Machine learning has a wide range of applications in various fields, from image recognition and natural language processing to recommendation systems and fraud detection, and it is changing the way we live. There are many different methods and theories in the field of machine learning, among which the five most influential methods are called the "Five Schools of Machine Learning". The five major schools are the symbolic school, the connectionist school, the evolutionary school, the Bayesian school and the analogy school. 1. Symbolism, also known as symbolism, emphasizes the use of symbols for logical reasoning and expression of knowledge. This school of thought believes that learning is a process of reverse deduction, through existing
 Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
May 30, 2024 pm 01:24 PM
Is Flash Attention stable? Meta and Harvard found that their model weight deviations fluctuated by orders of magnitude
May 30, 2024 pm 01:24 PM
MetaFAIR teamed up with Harvard to provide a new research framework for optimizing the data bias generated when large-scale machine learning is performed. It is known that the training of large language models often takes months and uses hundreds or even thousands of GPUs. Taking the LLaMA270B model as an example, its training requires a total of 1,720,320 GPU hours. Training large models presents unique systemic challenges due to the scale and complexity of these workloads. Recently, many institutions have reported instability in the training process when training SOTA generative AI models. They usually appear in the form of loss spikes. For example, Google's PaLM model experienced up to 20 loss spikes during the training process. Numerical bias is the root cause of this training inaccuracy,




