Improved RMSprop algorithm

RMSprop is a widely used optimizer for updating the weights of neural networks. It was proposed by Geoffrey Hinton et al. in 2012 and is the predecessor of the Adam optimizer. The emergence of the RMSprop optimizer is mainly to solve some problems encountered in the SGD gradient descent algorithm, such as gradient disappearance and gradient explosion. By using the RMSprop optimizer, the learning rate can be effectively adjusted and the weights adaptively updated, thereby improving the training effect of the deep learning model.
The core idea of the RMSprop optimizer is to perform a weighted average of gradients so that gradients at different time steps have different effects on the update of weights. Specifically, RMSprop computes an exponentially weighted average of the squared gradients of each parameter and divides it by the square root of the average gradient. This square root serves as the denominator to normalize the historical gradient of each parameter, thereby making the update amount of each parameter smoother. In addition, RMSprop can also adjust the learning rate so that it gradually decreases during the training process to improve the model's convergence speed and generalization ability. In this way, RMSprop can effectively handle changes in gradients and help the model better adapt to different data distributions and optimization goals.
Specifically, the update formula of the RMSprop optimizer is as follows:
\begin{aligned}
v_t&=\gamma v_{t-1}+(1-\gamma)(\nabla J(\theta_t))^2\
\theta_{t+1}&=\theta_t-\frac{\eta}{\sqrt{v_t}+\epsilon}\nabla J(\theta_t)
\end{aligned}Where, v_t represents the The exponentially weighted average of the squared gradients of t time steps, usually calculated using the decay rate \gamma=0.9. The learning rate \eta is used to control the step size of parameter update, and \epsilon is a small constant used to prevent division by 0 from occurring. These parameters play an important role in the gradient descent algorithm. By adjusting their values, the optimization process can be finely adjusted and optimized.
The main advantage of the RMSprop optimizer is that it can adaptively adjust the learning rate of each parameter, thereby reducing oscillations and instability during the training process. Compared with traditional gradient descent algorithms, RMSprop can converge faster and have better generalization capabilities. In addition, RMSprop can also handle sparse gradients, making it more efficient when processing large data sets.
However, RMSprop also has some shortcomings. First, the learning rate of RMSprop may be too small, causing the model to converge slowly. Second, RMSprop may be affected by noisy gradients, resulting in poor model performance. In addition, the performance of RMSprop is also affected by hyperparameters such as initial learning rate, decay rate, constant $\epsilon$, etc., and requires empirical parameter adjustment.
Can the rmsprop optimizer prevent overfitting?
The RMSprop optimizer can help alleviate overfitting problems in some cases , but it does not completely solve overfitting. The RMSprop optimizer adaptively adjusts the learning rate of each parameter to converge to the optimal solution faster. This helps prevent the model from overfitting on the training set, but does not guarantee that the model will not overfit on the test set. Therefore, in order to effectively alleviate the overfitting problem, other techniques such as regularization, dropout, etc. are usually required.
Usage of rmsprop optimizer
The RMSprop optimizer is a common gradient descent optimizer that can be used to train neural networks. The following are the general steps for using the RMSprop optimizer:
1. Import the required libraries and datasets
2. Build the neural network model
3. Initialize the RMSprop optimizer, specify the learning rate and other hyperparameters
4. Compile the model, specify the loss function and evaluation indicators
5. Train the model, specify the training data set, batch size, number of training cycles and other parameters
6. Evaluate the model performance and use the test Data set for evaluation
7. Adjust model architecture, hyperparameters, etc. to further improve model performance
The following is an implementation using Keras API Example of RMSprop optimizer:
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import RMSprop
from keras.datasets import mnist
# Load MNIST dataset
(train_images, train_labels), (test_images, test_labels) = mnist.load_data()
# Preprocess the data
train_images = train_images.reshape((60000, 784))
train_images = train_images.astype('float32') / 255
test_images = test_images.reshape((10000, 784))
test_images = test_images.astype('float32') / 255
# Build the model
model = Sequential()
model.add(Dense(512, activation='relu', input_shape=(784,)))
model.add(Dense(10, activation='softmax'))
# Initialize RMSprop optimizer
optimizer = RMSprop(lr=0.001, rho=0.9)
# Compile the model
model.compile(optimizer=optimizer,
loss='categorical_crossentropy',
metrics=['accuracy'])
# Train the model
model.fit(train_images, train_labels, epochs=5, batch_size=128)
# Evaluate the model
test_loss, test_acc = model.evaluate(test_images, test_labels)
print('Test accuracy:', test_acc)In the above code, we first load the MNIST dataset and preprocess it. We then use Keras to build a neural network model with two fully connected layers and optimize it using the RMSprop optimizer. We specified a learning rate of 0.001 and a rho parameter of 0.9. Next, we compile the model using cross-entropy as the loss function and accuracy as the evaluation metric. We then trained the model using the training dataset, specifying the number of training epochs as 5 and the batch size as 128. Finally, we evaluate the model performance using the test dataset and output the test accuracy.
The above is the detailed content of Improved RMSprop algorithm. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1387
1387
 52
52
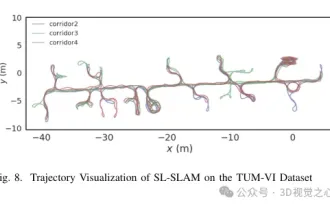 Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Written previously, today we discuss how deep learning technology can improve the performance of vision-based SLAM (simultaneous localization and mapping) in complex environments. By combining deep feature extraction and depth matching methods, here we introduce a versatile hybrid visual SLAM system designed to improve adaptation in challenging scenarios such as low-light conditions, dynamic lighting, weakly textured areas, and severe jitter. sex. Our system supports multiple modes, including extended monocular, stereo, monocular-inertial, and stereo-inertial configurations. In addition, it also analyzes how to combine visual SLAM with deep learning methods to inspire other research. Through extensive experiments on public datasets and self-sampled data, we demonstrate the superiority of SL-SLAM in terms of positioning accuracy and tracking robustness.
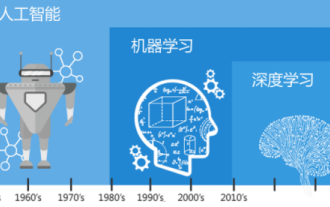 Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
In today's wave of rapid technological changes, Artificial Intelligence (AI), Machine Learning (ML) and Deep Learning (DL) are like bright stars, leading the new wave of information technology. These three words frequently appear in various cutting-edge discussions and practical applications, but for many explorers who are new to this field, their specific meanings and their internal connections may still be shrouded in mystery. So let's take a look at this picture first. It can be seen that there is a close correlation and progressive relationship between deep learning, machine learning and artificial intelligence. Deep learning is a specific field of machine learning, and machine learning
 Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Almost 20 years have passed since the concept of deep learning was proposed in 2006. Deep learning, as a revolution in the field of artificial intelligence, has spawned many influential algorithms. So, what do you think are the top 10 algorithms for deep learning? The following are the top algorithms for deep learning in my opinion. They all occupy an important position in terms of innovation, application value and influence. 1. Deep neural network (DNN) background: Deep neural network (DNN), also called multi-layer perceptron, is the most common deep learning algorithm. When it was first invented, it was questioned due to the computing power bottleneck. Until recent years, computing power, The breakthrough came with the explosion of data. DNN is a neural network model that contains multiple hidden layers. In this model, each layer passes input to the next layer and
 A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
The bidirectional LSTM model is a neural network used for text classification. Below is a simple example demonstrating how to use bidirectional LSTM for text classification tasks. First, we need to import the required libraries and modules: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
Editor | Radish Skin Since the release of the powerful AlphaFold2 in 2021, scientists have been using protein structure prediction models to map various protein structures within cells, discover drugs, and draw a "cosmic map" of every known protein interaction. . Just now, Google DeepMind released the AlphaFold3 model, which can perform joint structure predictions for complexes including proteins, nucleic acids, small molecules, ions and modified residues. The accuracy of AlphaFold3 has been significantly improved compared to many dedicated tools in the past (protein-ligand interaction, protein-nucleic acid interaction, antibody-antigen prediction). This shows that within a single unified deep learning framework, it is possible to achieve
 How to use CNN and Transformer hybrid models to improve performance
Jan 24, 2024 am 10:33 AM
How to use CNN and Transformer hybrid models to improve performance
Jan 24, 2024 am 10:33 AM
Convolutional Neural Network (CNN) and Transformer are two different deep learning models that have shown excellent performance on different tasks. CNN is mainly used for computer vision tasks such as image classification, target detection and image segmentation. It extracts local features on the image through convolution operations, and performs feature dimensionality reduction and spatial invariance through pooling operations. In contrast, Transformer is mainly used for natural language processing (NLP) tasks such as machine translation, text classification, and speech recognition. It uses a self-attention mechanism to model dependencies in sequences, avoiding the sequential computation in traditional recurrent neural networks. Although these two models are used for different tasks, they have similarities in sequence modeling, so
 TensorFlow deep learning framework model inference pipeline for portrait cutout inference
Mar 26, 2024 pm 01:00 PM
TensorFlow deep learning framework model inference pipeline for portrait cutout inference
Mar 26, 2024 pm 01:00 PM
Overview In order to enable ModelScope users to quickly and conveniently use various models provided by the platform, a set of fully functional Python libraries are provided, which includes the implementation of ModelScope official models, as well as the necessary tools for using these models for inference, finetune and other tasks. Code related to data pre-processing, post-processing, effect evaluation and other functions, while also providing a simple and easy-to-use API and rich usage examples. By calling the library, users can complete tasks such as model reasoning, training, and evaluation by writing just a few lines of code. They can also quickly perform secondary development on this basis to realize their own innovative ideas. The algorithm model currently provided by the library is:
 Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Convolutional neural networks perform well in image denoising tasks. It utilizes the learned filters to filter the noise and thereby restore the original image. This article introduces in detail the image denoising method based on convolutional neural network. 1. Overview of Convolutional Neural Network Convolutional neural network is a deep learning algorithm that uses a combination of multiple convolutional layers, pooling layers and fully connected layers to learn and classify image features. In the convolutional layer, the local features of the image are extracted through convolution operations, thereby capturing the spatial correlation in the image. The pooling layer reduces the amount of calculation by reducing the feature dimension and retains the main features. The fully connected layer is responsible for mapping learned features and labels to implement image classification or other tasks. The design of this network structure makes convolutional neural networks useful in image processing and recognition.




