 Backend Development
Backend Development
 Python Tutorial
Python Tutorial
 Parse the Ford-Fulkerson algorithm and implement it through Python
Parse the Ford-Fulkerson algorithm and implement it through Python
Parse the Ford-Fulkerson algorithm and implement it through Python
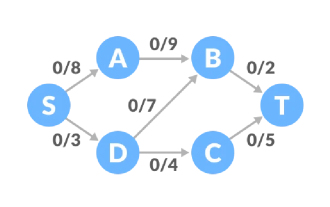
The Ford-Fulkerson algorithm is a greedy algorithm used to calculate the maximum flow in the network. The principle is to find an augmenting path with a positive remaining capacity. As long as the augmenting path is found, you can continue to add paths and calculate traffic. Until the augmenting path no longer exists, the maximum flow rate can be obtained.
Terminology of Ford-Fulkerson algorithm
Remaining capacity: It is the capacity minus the flow. In the Ford-Fulkerson algorithm, the remaining capacity is a positive number before it can continue to be used as a path.
Residual network: It is a network with the same vertices and edges, using residual capacity as capacity.
Augmented path: It is the path from the source point to the receiving point in the residual graph, with a final capacity of 0.
Ford-Fulkerson algorithm principle example
The concept may not be very clear. Let’s look at an example. The initial traffic of all edges of the flow network is 0, and there is a corresponding capacity upper limit. Set The starting point is S and the receiving point is T.
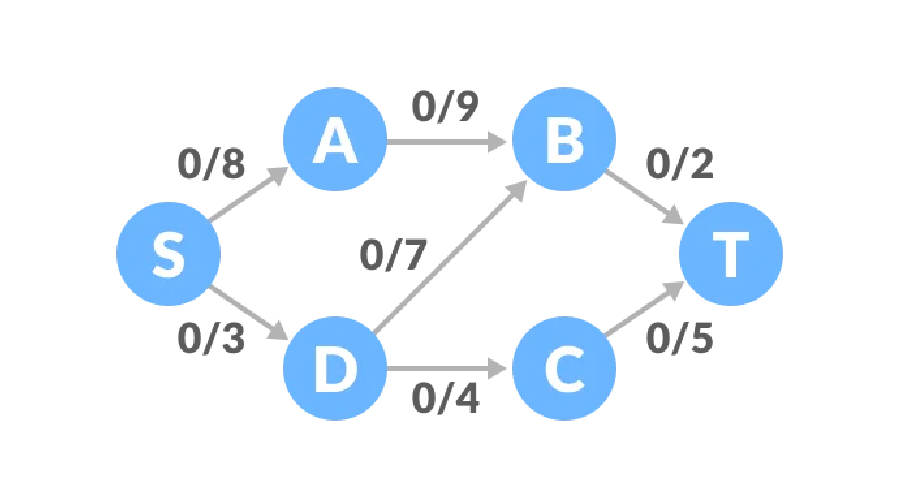
Path one, the remaining capacity of the S-A-B-T path is 8, 9, 2, and the minimum value is 2, so the traffic of path one is 2. At this time The network diagram has a flow rate of 2.
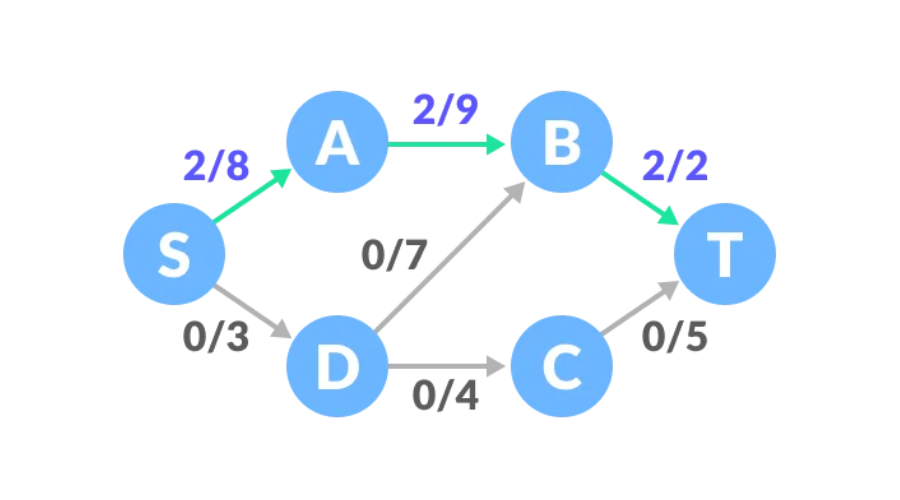
Path two, the remaining capacity of the S-D-C-T path is 3, 4, 5, and the minimum value is 3, so we can increase the traffic by 3. At this time The traffic of the network is 5.
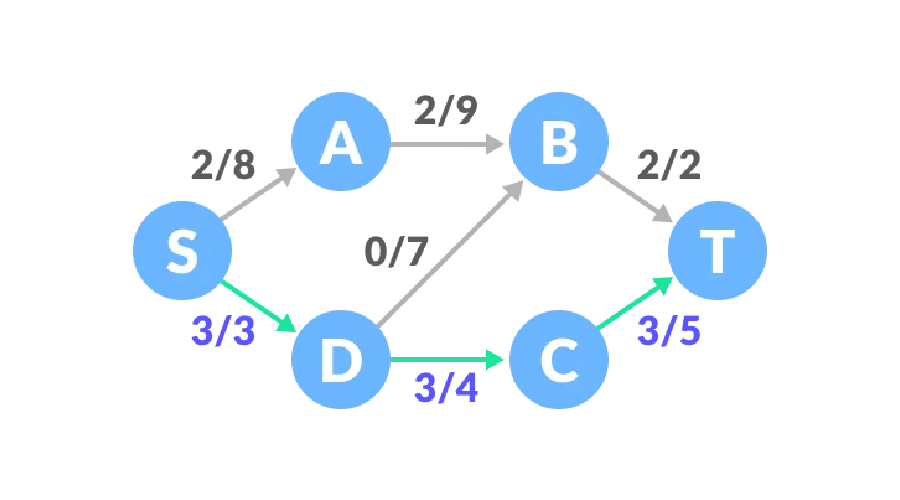
Path three, the remaining capacity of the S-A-B-D-C-T path is 6, 7, 7, 1, 2, and the minimum value is 1, so the traffic increases by 1, which The network traffic at this time is 6.
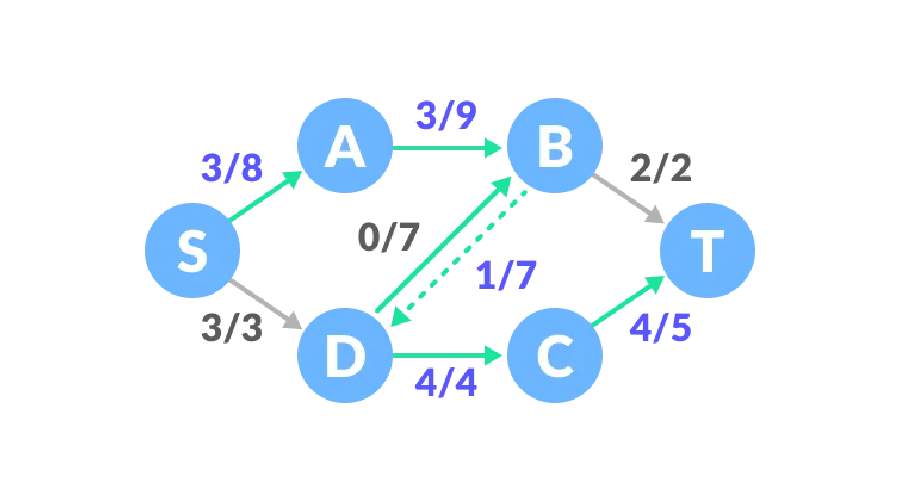
At this point, there is no positive remaining capacity, and the maximum flow of the flow network is 6.
Python implements Ford-Fulkerson algorithm
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def searching_algo_BFS(self, s, t, parent):
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
def ford_fulkerson(self, source, sink):
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0
sink = 5
print("Max Flow: %d " % g.ford_fulkerson(source, sink))The above is the detailed content of Parse the Ford-Fulkerson algorithm and implement it through Python. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 How to implement greedy algorithm in C#
Sep 19, 2023 am 11:48 AM
How to implement greedy algorithm in C#
Sep 19, 2023 am 11:48 AM
How to implement the greedy algorithm in C# The greedy algorithm (Greedy algorithm) is a commonly used problem-solving method. It selects the current optimal solution every time in the hope of obtaining the global optimal solution. In C#, we can use greedy algorithms to solve many practical problems. This article will introduce how to implement the greedy algorithm in C# and provide specific code examples. 1. Basic principles of greedy algorithm The basic idea of greedy algorithm is to choose the current optimal solution every time, regardless of the possible impact of subsequent steps. This kind of thinking
 How to implement an efficient solution to the least coin change problem in PHP using the greedy algorithm?
Sep 19, 2023 am 10:22 AM
How to implement an efficient solution to the least coin change problem in PHP using the greedy algorithm?
Sep 19, 2023 am 10:22 AM
How to implement an efficient solution to the least coin change problem in PHP using the greedy algorithm? Introduction: In daily life, we often need to make change, especially when shopping or trading. To use as few coins as possible, the change amount should be combined using as few coins as possible. In computer programming, we can use a greedy algorithm to solve this problem to get an efficient solution. This article will introduce how to use the greedy algorithm in PHP to achieve an efficient solution to the minimum coin change problem, and provide corresponding code examples.
 Parse the Ford-Fulkerson algorithm and implement it through Python
Jan 22, 2024 pm 08:09 PM
Parse the Ford-Fulkerson algorithm and implement it through Python
Jan 22, 2024 pm 08:09 PM
The Ford-Fulkerson algorithm is a greedy algorithm used to calculate the maximum flow rate in a network. The principle is to find an augmenting path with a positive remaining capacity. As long as the augmenting path is found, you can continue to add paths and calculate traffic. Until the augmenting path no longer exists, the maximum flow rate can be obtained. The term remaining capacity of the Ford-Fulkerson algorithm is to subtract the flow from the capacity. In the Ford-Fulkerson algorithm, the remaining capacity is a positive number before it can continue to be used as a path. Residual network: It is a network with the same vertices and edges, using residual capacity as capacity. Augmented path: It is the path from the source point to the receiving point in the residual graph, with a final capacity of 0. A possible outline of the Ford-Fulkerson algorithm principle example
 How to implement greedy algorithm using Python?
Sep 19, 2023 am 11:43 AM
How to implement greedy algorithm using Python?
Sep 19, 2023 am 11:43 AM
How to implement greedy algorithm using Python? Greedy Algorithm is a simple and effective algorithm suitable for solving problems with optimal substructure properties. It takes the best choice in the current state in each step of selection, hoping to find the global optimal solution. In this article, we will introduce how to use Python to implement the greedy algorithm, with specific code examples. 1. The basic idea of the greedy algorithm The basic idea of the greedy algorithm is to select the optimal solution in the current state at each step, and then
 How to write a greedy algorithm using PHP
Jul 07, 2023 pm 03:45 PM
How to write a greedy algorithm using PHP
Jul 07, 2023 pm 03:45 PM
How to use PHP to write a greedy algorithm Greedy algorithm (Greedy algorithm) is a simple and effective algorithm used to solve a type of optimization problem. Its basic idea is to make the choice at each step that seems best at the moment, without regard to future consequences. This article will introduce how to write a greedy algorithm using PHP and provide relevant code examples. 1. Problem Description Before explaining the greedy algorithm, let us first define a specific problem for a better understanding. Suppose there is a set of tasks, each task has a start
 Greedy algorithm and its implementation in C++
Aug 22, 2023 am 10:04 AM
Greedy algorithm and its implementation in C++
Aug 22, 2023 am 10:04 AM
The greedy algorithm is a commonly used algorithm idea and is widely used in many problems. The core idea is to only consider the immediate optimal solution when making a decision at each step, without considering the long-term impact. In C++, the implementation of greedy algorithms often involves basic operations such as sorting and data processing. Below, we will introduce the idea of greedy algorithm and its implementation in C++ for several typical problems. 1. Activity Scheduling Problem Given a set of activities, each activity has its start time and end time, and a person can only participate in one activity at a time.
 How to implement greedy algorithm using java
Sep 19, 2023 am 11:13 AM
How to implement greedy algorithm using java
Sep 19, 2023 am 11:13 AM
How to use Java to implement greedy algorithm Greedy algorithm (GreedyAlgorithm) is an algorithmic idea for solving problems. Its characteristic is to select the current optimal solution at each step, hoping to eventually reach the global optimal solution through each local optimal solution. The simple and efficient characteristics of the greedy algorithm make it a commonly used algorithm when solving some optimization problems or certain specific problems. This article will introduce how to implement the greedy algorithm using Java and provide specific code examples. 1. The basic idea of greedy algorithm The basis of greedy algorithm
 C/C++ program for greedy algorithm to find the minimum number of coins
Sep 19, 2023 pm 11:01 PM
C/C++ program for greedy algorithm to find the minimum number of coins
Sep 19, 2023 pm 11:01 PM
The greedy algorithm is an algorithm used to find the optimal solution to a given problem. The greedy algorithm works by finding a local optimal solution for each part (the optimal solution to one part of the problem), thus showing that a global optimal solution can be found. In this problem, we will use the Greedy Algorithm algorithm to find the minimum number of coins/notes that can make up a given sum. For this we will consider all valid coins or banknotes, i.e. denominations {1,2,5,10,20,50,100,200,500,2000}. We need to return the number of coins/notes needed to make up the sum. Let us give a few examples to understand the context better - Example 1 - Input: 1231 Output: 7 Description - We need two 500 rupee notes



