Applying machine learning to implement moving averages

The concept of moving average
Moving average is a technical analysis method commonly used in machine learning. It is a statistical technique for analyzing time series data by calculating the average of consecutive data points within a sliding window. The main function of the moving average is to smooth the fluctuations of data, thereby reducing the impact of short-term fluctuations and noise on the data. By using moving averages, we can more easily identify trends and patterns in our data. This is very helpful in predicting future data trends and behavior. Therefore, moving averages are an important technical analysis tool in machine learning.
The moving average technique requires setting the window size, also known as the span, which determines the number of data points used in the calculation. The choice of window size has an impact on the smoothness of the average. A larger window size will result in a smoother average, but will respond slower to data changes. In contrast, a smaller window size provides a more sensitive response but is also susceptible to short-term fluctuations in the data. Therefore, there is a trade-off between smoothness and responsiveness. In addition, moving averages are sensitive to outliers and may not accurately reflect the underlying pattern of the data. Therefore, when using moving average techniques, you need to be aware of slow responses to changes in data and possible hysteresis.
Moving averages and optimization algorithms in machine learning
In machine learning, our goal is to adjust the parameters of the model to make the error between the model's prediction results and the actual target value minimize. To measure the size of the error, we summarize the performance of the model using an objective function, which is usually a mathematical expression. To achieve the goal of minimizing the objective function, we use an optimization algorithm to tune the parameters of the model.
One of the challenges of optimization is determining the appropriate learning rate, which determines the stride size in each iteration. A common solution is to use a moving average to adjust the learning rate.
Moving average involves calculating an exponentially weighted moving average of the objective function over time.
For example, first we define the necessary parameters.
Suppose J(t) is the objective function of iteration time t, and J_avg(t) is the moving average of iteration time t. In each iteration, the moving average is updated by the following equation:
J_avg(t 1)=beta*J_avg(t) (1-beta)*J(t 1)
Required To illustrate, in the above equation, Beta is a parameter that determines the weight given to the previous average. If Beta is close to 1, the moving average will change more slowly and rely more on past data. And if Beta is close to 0, the moving average changes will be more sensitive and focus more on the current iteration. Therefore, choosing an appropriate Beta value will directly affect the behavior of the moving average and the optimization process.
The learning rate is set to be inversely proportional to the square root of the moving average, so that when the average is large, the smaller it is, indicating that the model is close to the minimum; the smaller the average, the model is close to the minimum, and the model is far from minimum value. Calculate the learning rate using the following equation:
learning_rate=alpha/sqrt(J_avg(t))
where Alpha is the constant factor that determines the initial learning rate.
Now we can use the Python moving average algorithm, the code is as follows:
import numpy as np def moving_average_schedule(x_0,gradient,J,T,alpha,beta): J_avg=J(x_0) x=x_0 for t in range(T): learning_rate=alpha/np.sqrt(J_avg) x=x-learning_rate*gradient(x) J_avg=beta*J_avg+(1-beta)*J(x) return x
So far we have obtained the optimization parameters. Among them, x_0 is the initial optimization parameter, gradient(x) is a function that returns the gradient of the objective function at x, J(x) is a function that returns the value of the objective function at x, T is the number of iterations, and alpha determines the initial learning The constant factor of rate, beta is the moving average parameter. The final result x is the optimized parameter after T iterations.
In general, moving averages are a simple and effective way to schedule learning rates in optimization algorithms. Using the moving average of the objective function, the learning rate can be dynamically adjusted according to the convergence of the optimization process, which helps to improve the stability and efficiency of the optimization.
The above is the detailed content of Applying machine learning to implement moving averages. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 15 recommended open source free image annotation tools
Mar 28, 2024 pm 01:21 PM
15 recommended open source free image annotation tools
Mar 28, 2024 pm 01:21 PM
Image annotation is the process of associating labels or descriptive information with images to give deeper meaning and explanation to the image content. This process is critical to machine learning, which helps train vision models to more accurately identify individual elements in images. By adding annotations to images, the computer can understand the semantics and context behind the images, thereby improving the ability to understand and analyze the image content. Image annotation has a wide range of applications, covering many fields, such as computer vision, natural language processing, and graph vision models. It has a wide range of applications, such as assisting vehicles in identifying obstacles on the road, and helping in the detection and diagnosis of diseases through medical image recognition. . This article mainly recommends some better open source and free image annotation tools. 1.Makesens
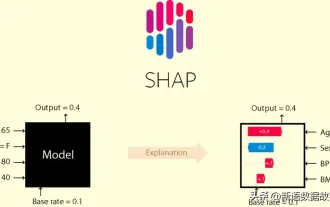 This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
This article will take you to understand SHAP: model explanation for machine learning
Jun 01, 2024 am 10:58 AM
In the fields of machine learning and data science, model interpretability has always been a focus of researchers and practitioners. With the widespread application of complex models such as deep learning and ensemble methods, understanding the model's decision-making process has become particularly important. Explainable AI|XAI helps build trust and confidence in machine learning models by increasing the transparency of the model. Improving model transparency can be achieved through methods such as the widespread use of multiple complex models, as well as the decision-making processes used to explain the models. These methods include feature importance analysis, model prediction interval estimation, local interpretability algorithms, etc. Feature importance analysis can explain the decision-making process of a model by evaluating the degree of influence of the model on the input features. Model prediction interval estimate
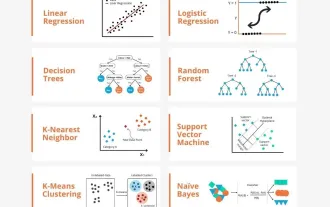 Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
Transparent! An in-depth analysis of the principles of major machine learning models!
Apr 12, 2024 pm 05:55 PM
In layman’s terms, a machine learning model is a mathematical function that maps input data to a predicted output. More specifically, a machine learning model is a mathematical function that adjusts model parameters by learning from training data to minimize the error between the predicted output and the true label. There are many models in machine learning, such as logistic regression models, decision tree models, support vector machine models, etc. Each model has its applicable data types and problem types. At the same time, there are many commonalities between different models, or there is a hidden path for model evolution. Taking the connectionist perceptron as an example, by increasing the number of hidden layers of the perceptron, we can transform it into a deep neural network. If a kernel function is added to the perceptron, it can be converted into an SVM. this one
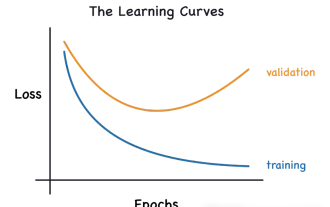 Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
Identify overfitting and underfitting through learning curves
Apr 29, 2024 pm 06:50 PM
This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves. Underfitting and overfitting 1. Overfitting If a model is overtrained on the data so that it learns noise from it, then the model is said to be overfitting. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score. Slightly modified: "Cause of overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set as a training set may not represent the correct representation of all data." 2. Underfitting Heru
 The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
The evolution of artificial intelligence in space exploration and human settlement engineering
Apr 29, 2024 pm 03:25 PM
In the 1950s, artificial intelligence (AI) was born. That's when researchers discovered that machines could perform human-like tasks, such as thinking. Later, in the 1960s, the U.S. Department of Defense funded artificial intelligence and established laboratories for further development. Researchers are finding applications for artificial intelligence in many areas, such as space exploration and survival in extreme environments. Space exploration is the study of the universe, which covers the entire universe beyond the earth. Space is classified as an extreme environment because its conditions are different from those on Earth. To survive in space, many factors must be considered and precautions must be taken. Scientists and researchers believe that exploring space and understanding the current state of everything can help understand how the universe works and prepare for potential environmental crises
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Explainable AI: Explaining complex AI/ML models
Jun 03, 2024 pm 10:08 PM
Translator | Reviewed by Li Rui | Chonglou Artificial intelligence (AI) and machine learning (ML) models are becoming increasingly complex today, and the output produced by these models is a black box – unable to be explained to stakeholders. Explainable AI (XAI) aims to solve this problem by enabling stakeholders to understand how these models work, ensuring they understand how these models actually make decisions, and ensuring transparency in AI systems, Trust and accountability to address this issue. This article explores various explainable artificial intelligence (XAI) techniques to illustrate their underlying principles. Several reasons why explainable AI is crucial Trust and transparency: For AI systems to be widely accepted and trusted, users need to understand how decisions are made
 Outlook on future trends of Golang technology in machine learning
May 08, 2024 am 10:15 AM
Outlook on future trends of Golang technology in machine learning
May 08, 2024 am 10:15 AM
The application potential of Go language in the field of machine learning is huge. Its advantages are: Concurrency: It supports parallel programming and is suitable for computationally intensive operations in machine learning tasks. Efficiency: The garbage collector and language features ensure that the code is efficient, even when processing large data sets. Ease of use: The syntax is concise, making it easy to learn and write machine learning applications.






