Convolution kernel in neural network

In neural networks, filters usually refer to the convolution kernels in convolutional neural networks. The convolution kernel is a small matrix used to perform convolution operations on the input image to extract features in the image. The convolution operation can be regarded as a filtering operation. By performing a convolution operation on the input data, the spatial structure information in the data can be captured. This operation is widely used in the fields of image processing and computer vision, and can be used for tasks such as edge detection, feature extraction, and target recognition. By adjusting the size and weight of the convolution kernel, the characteristics of the filter can be changed to adapt to different feature extraction needs.
In a convolutional neural network, each convolutional layer contains multiple filters, and each filter is responsible for extracting different features. These features can be used to identify objects, textures, edges and other information in images. When training a neural network, the weights of the filters are optimized so that the neural network can better identify features in the input image.
In addition to filters in convolutional neural networks, there are other types of filters, such as pooling filters and local response normalization filters. The pooling filter downsamples the input data to reduce the data dimension and improve computing efficiency. The local response normalization filter enhances the sensitivity of the neural network to small changes in the input data. These filters help the neural network better understand the characteristics of the input data and improve performance.
How neural network filters work
In neural networks, filters refer to the convolution kernels in convolutional neural networks. Their role is to perform convolution operations on input data to extract features in the data. The convolution operation is essentially a filtering operation. By performing a convolution operation on the input data, we can capture the spatial structure information in the data. This operation can be viewed as a weighted summation of the convolution kernel and the input data. Through different filters, we can capture different characteristics of the data, thereby achieving effective processing and analysis of the data.
In a convolutional neural network, each convolutional layer contains multiple filters that can extract different features. The weights of these filters are optimized during training to enable the neural network to more accurately identify features in the input data.
Convolutional neural networks use multiple filters to extract multiple different features at the same time to understand the input data more comprehensively. These filters are key components of neural networks for tasks such as image classification and target detection.
What is the function of the neural network filter
The main function of the filter in the neural network is to extract features from the input data.
In a convolutional neural network, each convolutional layer contains multiple filters, and each filter can extract different features. By using multiple filters, convolutional neural networks are able to extract multiple different features simultaneously to better understand the input data. During the training process, the weights of the filters are continuously optimized so that the neural network can better identify features in the input data.
Filters play a vital role in deep learning. They can capture spatial structural information in the input data, such as features such as edges, texture, and shape. By stacking multiple convolutional layers, we can build a deep neural network to extract more high-level features, such as various attributes and relationships of objects. These features play an important role in tasks such as image classification, target detection, and image generation. Therefore, filters in neural networks play an important role in deep learning.
The size and step size of the neural network filter
The size and step size of the filter in the neural network are two important parameters in the convolutional neural network.
The size of the filter refers to the size of the convolution kernel, which is usually a square or rectangular matrix. In a convolutional neural network, each convolutional layer contains multiple filters, and each filter can extract different features. The size of the filter affects the receptive field of the convolution operation, that is, the size of the area where the convolution operation can see the input data. Usually, the size of the convolution kernel is a hyperparameter, and the optimal size needs to be determined through experiments.
The step size refers to the step size of the convolution kernel moving on the input data. The size of the step size determines the output size of the convolution operation. When the stride is 1, the output size of the convolution operation is the same as the input size. When the stride is greater than 1, the output size of the convolution operation shrinks. The step size is also a hyperparameter, and experiments are required to determine the optimal size.
Normally, the size and step size of the filter are two important parameters in the convolutional neural network, and they will directly affect the performance and computational efficiency of the neural network. When training a neural network, experiments are needed to determine the optimal filter size and step size to improve the performance of the neural network.
The above is the detailed content of Convolution kernel in neural network. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 Explore the concepts, differences, advantages and disadvantages of RNN, LSTM and GRU
Jan 22, 2024 pm 07:51 PM
Explore the concepts, differences, advantages and disadvantages of RNN, LSTM and GRU
Jan 22, 2024 pm 07:51 PM
In time series data, there are dependencies between observations, so they are not independent of each other. However, traditional neural networks treat each observation as independent, which limits the model's ability to model time series data. To solve this problem, Recurrent Neural Network (RNN) was introduced, which introduced the concept of memory to capture the dynamic characteristics of time series data by establishing dependencies between data points in the network. Through recurrent connections, RNN can pass previous information into the current observation to better predict future values. This makes RNN a powerful tool for tasks involving time series data. But how does RNN achieve this kind of memory? RNN realizes memory through the feedback loop in the neural network. This is the difference between RNN and traditional neural network.
 Calculating floating point operands (FLOPS) for neural networks
Jan 22, 2024 pm 07:21 PM
Calculating floating point operands (FLOPS) for neural networks
Jan 22, 2024 pm 07:21 PM
FLOPS is one of the standards for computer performance evaluation, used to measure the number of floating point operations per second. In neural networks, FLOPS is often used to evaluate the computational complexity of the model and the utilization of computing resources. It is an important indicator used to measure the computing power and efficiency of a computer. A neural network is a complex model composed of multiple layers of neurons used for tasks such as data classification, regression, and clustering. Training and inference of neural networks requires a large number of matrix multiplications, convolutions and other calculation operations, so the computational complexity is very high. FLOPS (FloatingPointOperationsperSecond) can be used to measure the computational complexity of neural networks to evaluate the computational resource usage efficiency of the model. FLOP
 A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
The bidirectional LSTM model is a neural network used for text classification. Below is a simple example demonstrating how to use bidirectional LSTM for text classification tasks. First, we need to import the required libraries and modules: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 Definition and structural analysis of fuzzy neural network
Jan 22, 2024 pm 09:09 PM
Definition and structural analysis of fuzzy neural network
Jan 22, 2024 pm 09:09 PM
Fuzzy neural network is a hybrid model that combines fuzzy logic and neural networks to solve fuzzy or uncertain problems that are difficult to handle with traditional neural networks. Its design is inspired by the fuzziness and uncertainty in human cognition, so it is widely used in control systems, pattern recognition, data mining and other fields. The basic architecture of fuzzy neural network consists of fuzzy subsystem and neural subsystem. The fuzzy subsystem uses fuzzy logic to process input data and convert it into fuzzy sets to express the fuzziness and uncertainty of the input data. The neural subsystem uses neural networks to process fuzzy sets for tasks such as classification, regression or clustering. The interaction between the fuzzy subsystem and the neural subsystem makes the fuzzy neural network have more powerful processing capabilities and can
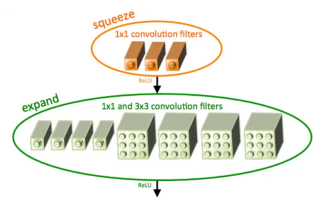 Introduction to SqueezeNet and its characteristics
Jan 22, 2024 pm 07:15 PM
Introduction to SqueezeNet and its characteristics
Jan 22, 2024 pm 07:15 PM
SqueezeNet is a small and precise algorithm that strikes a good balance between high accuracy and low complexity, making it ideal for mobile and embedded systems with limited resources. In 2016, researchers from DeepScale, University of California, Berkeley, and Stanford University proposed SqueezeNet, a compact and efficient convolutional neural network (CNN). In recent years, researchers have made several improvements to SqueezeNet, including SqueezeNetv1.1 and SqueezeNetv2.0. Improvements in both versions not only increase accuracy but also reduce computational costs. Accuracy of SqueezeNetv1.1 on ImageNet dataset
 Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Convolutional neural networks perform well in image denoising tasks. It utilizes the learned filters to filter the noise and thereby restore the original image. This article introduces in detail the image denoising method based on convolutional neural network. 1. Overview of Convolutional Neural Network Convolutional neural network is a deep learning algorithm that uses a combination of multiple convolutional layers, pooling layers and fully connected layers to learn and classify image features. In the convolutional layer, the local features of the image are extracted through convolution operations, thereby capturing the spatial correlation in the image. The pooling layer reduces the amount of calculation by reducing the feature dimension and retains the main features. The fully connected layer is responsible for mapping learned features and labels to implement image classification or other tasks. The design of this network structure makes convolutional neural networks useful in image processing and recognition.
 Steps to write a simple neural network using Rust
Jan 23, 2024 am 10:45 AM
Steps to write a simple neural network using Rust
Jan 23, 2024 am 10:45 AM
Rust is a systems-level programming language focused on safety, performance, and concurrency. It aims to provide a safe and reliable programming language suitable for scenarios such as operating systems, network applications, and embedded systems. Rust's security comes primarily from two aspects: the ownership system and the borrow checker. The ownership system enables the compiler to check code for memory errors at compile time, thus avoiding common memory safety issues. By forcing checking of variable ownership transfers at compile time, Rust ensures that memory resources are properly managed and released. The borrow checker analyzes the life cycle of the variable to ensure that the same variable will not be accessed by multiple threads at the same time, thereby avoiding common concurrency security issues. By combining these two mechanisms, Rust is able to provide
 causal convolutional neural network
Jan 24, 2024 pm 12:42 PM
causal convolutional neural network
Jan 24, 2024 pm 12:42 PM
Causal convolutional neural network is a special convolutional neural network designed for causality problems in time series data. Compared with conventional convolutional neural networks, causal convolutional neural networks have unique advantages in retaining the causal relationship of time series and are widely used in the prediction and analysis of time series data. The core idea of causal convolutional neural network is to introduce causality in the convolution operation. Traditional convolutional neural networks can simultaneously perceive data before and after the current time point, but in time series prediction, this may lead to information leakage problems. Because the prediction results at the current time point will be affected by the data at future time points. The causal convolutional neural network solves this problem. It can only perceive the current time point and previous data, but cannot perceive future data.




