
二叉树是一种树状数据结构,其中每个父节点最多可以有两个子节点。
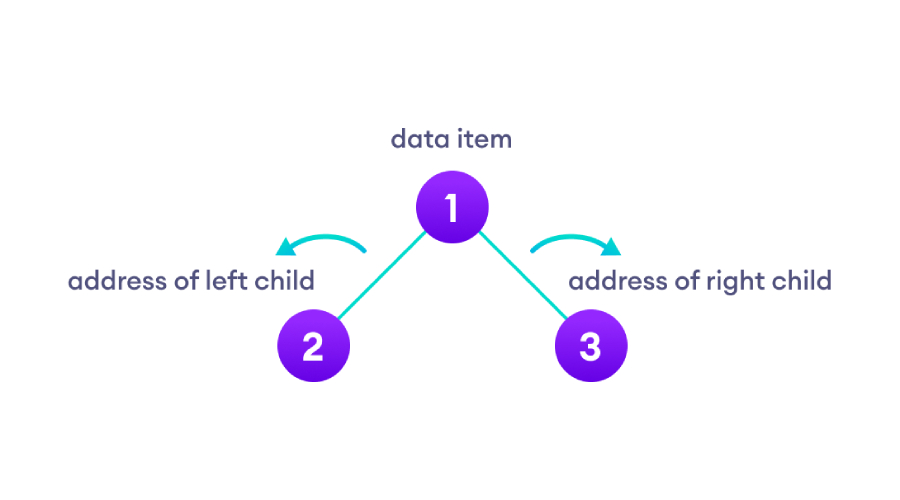
完全二叉树是一种特殊类型的二叉树,其父节点存在2种情况,要么有2个子节点,要么没有子节点,详情如下图:
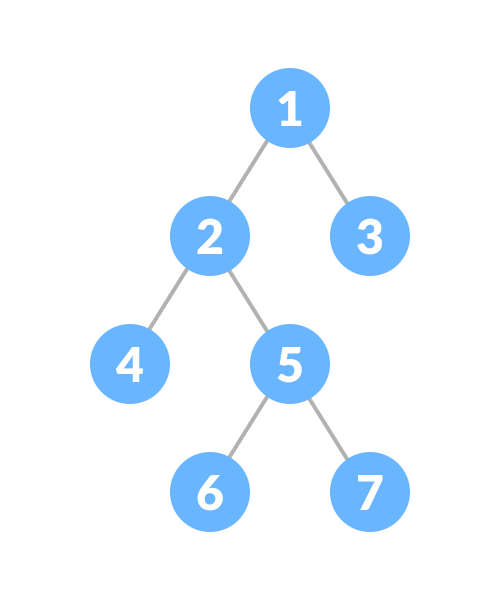
1、叶数为i+1
2、节点总数为2i+1
3、内部节点数为(n–1)/2
4、叶数为(n+1)/2
5、节点总数为2l–1
6、内部节点数为l–1
7、叶子的数量最多2^λ-1
class Node:
def __init__(self,item):
self.item=item
self.leftChild=None
self.rightChild=None
def isFullTree(root):
if root is None:
return True
if root.leftChild is None and root.rightChild is None:
return True
if root.leftChild is not None and root.rightChild is not None:
return(isFullTree(root.leftChild)and isFullTree(root.rightChild))
return False
root=Node(1)
root.rightChild=Node(3)
root.leftChild=Node(2)
root.leftChild.leftChild=Node(4)
root.leftChild.rightChild=Node(5)
root.leftChild.rightChild.leftChild=Node(6)
root.leftChild.rightChild.rightChild=Node(7)
if isFullTree(root):
print("The tree is a full binary tree")
else:
print("The tree is not a full binary tree")完美二叉树的每个内部节点都恰好有两个子节点,并且所有叶节点都在同一级别,如下图:
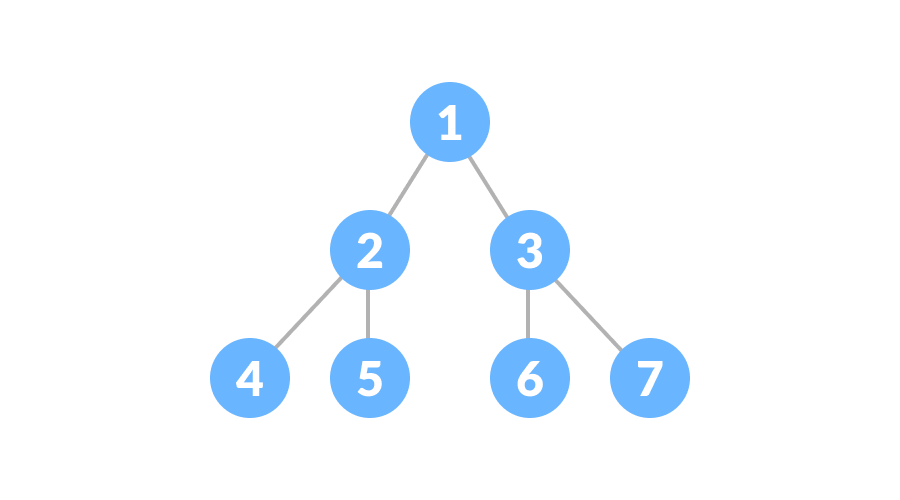
1、高度为h的完美二叉树有2^(h+1)–1个节点
2、具有n个节点的完美二叉树的高度为log(n+1)–1=Θ(ln(n))。
3、高度为h的完美二叉树具有2^h节点
4、完美二叉树中节点的平均深度为Θ(ln(n))。
class newNode:
def __init__(self,k):
self.key=k
self.right=self.left=None
def calculateDepth(node):
d=0
while(node is not None):
d+=1
node=node.left
return d
def is_perfect(root,d,level=0):
if(root is None):
return True
if(root.left is None and root.right is None):
return(d==level+1)
if(root.left is None or root.right is None):
return False
return(is_perfect(root.left,d,level+1)and
is_perfect(root.right,d,level+1))
root=None
root=newNode(1)
root.left=newNode(2)
root.right=newNode(3)
root.left.left=newNode(4)
root.left.right=newNode(5)
if(is_perfect(root,calculateDepth(root))):
print("The tree is a perfect binary tree")
else:
print("The tree is not a perfect binary tree")退化或病态树只具有左或右单个子节点的二叉树,如下图:
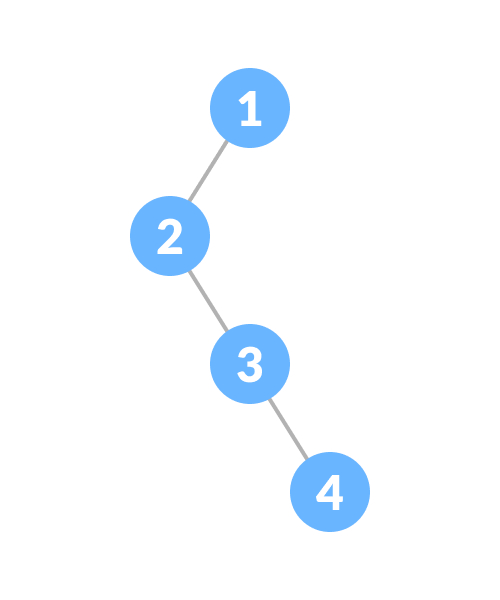
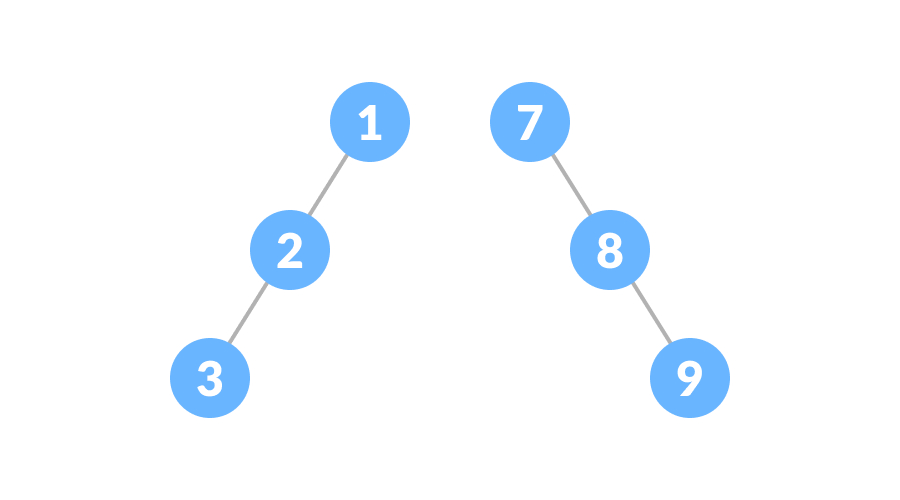
倾斜二叉树要么由左节点支配,要么由右节点支配。因此,有左二叉树和右二叉树两种类型,如下图:
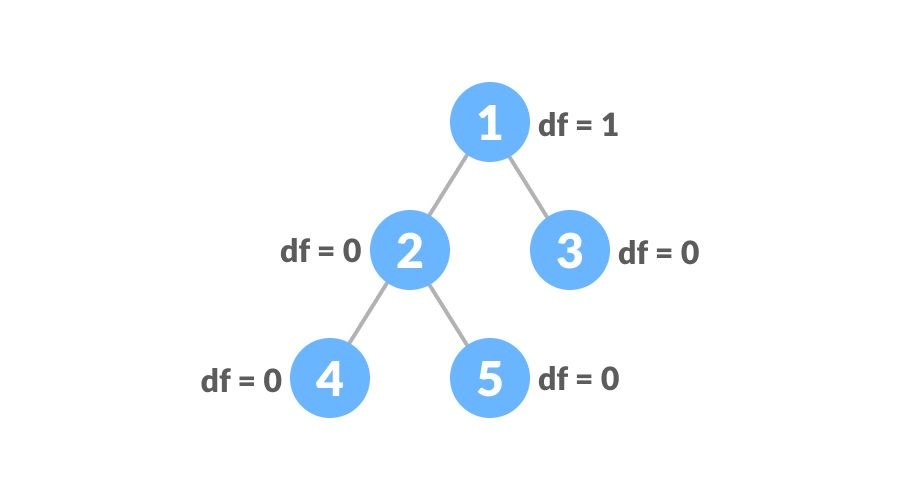
平衡二叉树每个节点的左子树和右子树的高度之差为0或1,如下图:
class Node: def __init__(self,data): self.data=data self.left=self.right=None class Height: def __init__(self): self.height=0 def isHeightBalanced(root,height): left_height=Height() right_height=Height() if root is None: return True l=isHeightBalanced(root.left,left_height) r=isHeightBalanced(root.right,right_height) height.height=max(left_height.height,right_height.height)+1 if abs(left_height.height-right_height.height)<=1: return l and r return False height=Height() root=Node(1) root.left=Node(2) root.right=Node(3) root.left.left=Node(4) root.left.right=Node(5) if isHeightBalanced(root,height): print('The tree is balanced') else: print('The tree is not balanced')
The above is the detailed content of How to judge different types of binary trees using Python. For more information, please follow other related articles on the PHP Chinese website!




