What exactly does error mean in the residual module?

The residual module is a commonly used technique in deep learning, used to solve the problems of gradient disappearance and gradient explosion, and improve the accuracy and stability of the model. Its core is residual connection, which adds input data and output data to form a cross-layer connection, making it easier for the model to learn residual information. Error refers to the error at the residual junction. In the following, this concept will be explained in detail.
In deep learning, error usually refers to the difference between the predicted value of the training data and the true value, also known as the loss. In the residual module, the error calculation method is different from that of the ordinary neural network model, including the following two aspects:
1. Residual calculation error
The residual connection in the residual module implements cross-layer connections by adding input data and output data. At the residual join, we need to calculate the residual, which is the difference between the input data and the output data. In order to measure the error in residual calculation, indicators such as square error or mean square error are generally used. The squared error is the square of the difference between the predicted value and the true value, while the mean squared error is the average of the squared errors. By reducing the residual calculation error, we can know that the smaller the difference at the residual connection, the better the fitting effect of the model.
2. Residual propagation error
In the residual module, the residual connection not only adds the input data to the output data, Also propagates errors back to previous levels. Residual propagation error therefore refers to the error involved in propagating errors from the output layer back to previous layers. In traditional neural networks, errors can only be propagated forward from the output layer, while in the residual module, errors can be propagated forward and backward from the residual connection. This propagation method can make it easier for the model to learn the residual difference information, thereby improving the accuracy and stability of the model.
Therefore, during the training process, it is necessary to minimize the error at the residual connection while ensuring that the error can be effectively propagated back to the previous layers. In order to achieve this goal, the back propagation algorithm can be used to calculate the error gradient, and the model parameters can be updated through the optimization algorithm, so that the error is gradually reduced and the accuracy of the model is gradually improved.
It should be noted that the error under the residual module is relative to the ordinary neural network. It emphasizes the difference between input and output, while the ordinary neural network emphasizes The difference between input and prediction. Therefore, when designing and optimizing the residual module, it is necessary to consider how to effectively utilize the residual information to improve the expression and generalization capabilities of the model, thereby achieving better performance.
The above is the detailed content of What exactly does error mean in the residual module?. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
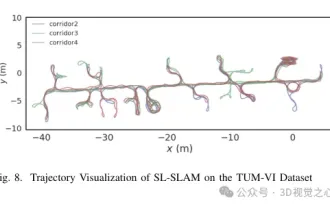 Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Beyond ORB-SLAM3! SL-SLAM: Low light, severe jitter and weak texture scenes are all handled
May 30, 2024 am 09:35 AM
Written previously, today we discuss how deep learning technology can improve the performance of vision-based SLAM (simultaneous localization and mapping) in complex environments. By combining deep feature extraction and depth matching methods, here we introduce a versatile hybrid visual SLAM system designed to improve adaptation in challenging scenarios such as low-light conditions, dynamic lighting, weakly textured areas, and severe jitter. sex. Our system supports multiple modes, including extended monocular, stereo, monocular-inertial, and stereo-inertial configurations. In addition, it also analyzes how to combine visual SLAM with deep learning methods to inspire other research. Through extensive experiments on public datasets and self-sampled data, we demonstrate the superiority of SL-SLAM in terms of positioning accuracy and tracking robustness.
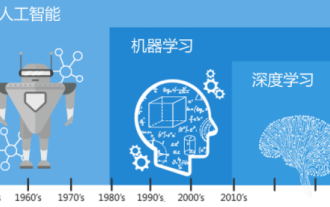 Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
Understand in one article: the connections and differences between AI, machine learning and deep learning
Mar 02, 2024 am 11:19 AM
In today's wave of rapid technological changes, Artificial Intelligence (AI), Machine Learning (ML) and Deep Learning (DL) are like bright stars, leading the new wave of information technology. These three words frequently appear in various cutting-edge discussions and practical applications, but for many explorers who are new to this field, their specific meanings and their internal connections may still be shrouded in mystery. So let's take a look at this picture first. It can be seen that there is a close correlation and progressive relationship between deep learning, machine learning and artificial intelligence. Deep learning is a specific field of machine learning, and machine learning
 Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Super strong! Top 10 deep learning algorithms!
Mar 15, 2024 pm 03:46 PM
Almost 20 years have passed since the concept of deep learning was proposed in 2006. Deep learning, as a revolution in the field of artificial intelligence, has spawned many influential algorithms. So, what do you think are the top 10 algorithms for deep learning? The following are the top algorithms for deep learning in my opinion. They all occupy an important position in terms of innovation, application value and influence. 1. Deep neural network (DNN) background: Deep neural network (DNN), also called multi-layer perceptron, is the most common deep learning algorithm. When it was first invented, it was questioned due to the computing power bottleneck. Until recent years, computing power, The breakthrough came with the explosion of data. DNN is a neural network model that contains multiple hidden layers. In this model, each layer passes input to the next layer and
 A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
A case study of using bidirectional LSTM model for text classification
Jan 24, 2024 am 10:36 AM
The bidirectional LSTM model is a neural network used for text classification. Below is a simple example demonstrating how to use bidirectional LSTM for text classification tasks. First, we need to import the required libraries and modules: importosimportnumpyasnpfromkeras.preprocessing.textimportTokenizerfromkeras.preprocessing.sequenceimportpad_sequencesfromkeras.modelsimportSequentialfromkeras.layersimportDense,Em
 AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
AlphaFold 3 is launched, comprehensively predicting the interactions and structures of proteins and all living molecules, with far greater accuracy than ever before
Jul 16, 2024 am 12:08 AM
Editor | Radish Skin Since the release of the powerful AlphaFold2 in 2021, scientists have been using protein structure prediction models to map various protein structures within cells, discover drugs, and draw a "cosmic map" of every known protein interaction. . Just now, Google DeepMind released the AlphaFold3 model, which can perform joint structure predictions for complexes including proteins, nucleic acids, small molecules, ions and modified residues. The accuracy of AlphaFold3 has been significantly improved compared to many dedicated tools in the past (protein-ligand interaction, protein-nucleic acid interaction, antibody-antigen prediction). This shows that within a single unified deep learning framework, it is possible to achieve
 How to use CNN and Transformer hybrid models to improve performance
Jan 24, 2024 am 10:33 AM
How to use CNN and Transformer hybrid models to improve performance
Jan 24, 2024 am 10:33 AM
Convolutional Neural Network (CNN) and Transformer are two different deep learning models that have shown excellent performance on different tasks. CNN is mainly used for computer vision tasks such as image classification, target detection and image segmentation. It extracts local features on the image through convolution operations, and performs feature dimensionality reduction and spatial invariance through pooling operations. In contrast, Transformer is mainly used for natural language processing (NLP) tasks such as machine translation, text classification, and speech recognition. It uses a self-attention mechanism to model dependencies in sequences, avoiding the sequential computation in traditional recurrent neural networks. Although these two models are used for different tasks, they have similarities in sequence modeling, so
 Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Image denoising using convolutional neural networks
Jan 23, 2024 pm 11:48 PM
Convolutional neural networks perform well in image denoising tasks. It utilizes the learned filters to filter the noise and thereby restore the original image. This article introduces in detail the image denoising method based on convolutional neural network. 1. Overview of Convolutional Neural Network Convolutional neural network is a deep learning algorithm that uses a combination of multiple convolutional layers, pooling layers and fully connected layers to learn and classify image features. In the convolutional layer, the local features of the image are extracted through convolution operations, thereby capturing the spatial correlation in the image. The pooling layer reduces the amount of calculation by reducing the feature dimension and retains the main features. The fully connected layer is responsible for mapping learned features and labels to implement image classification or other tasks. The design of this network structure makes convolutional neural networks useful in image processing and recognition.
 TensorFlow deep learning framework model inference pipeline for portrait cutout inference
Mar 26, 2024 pm 01:00 PM
TensorFlow deep learning framework model inference pipeline for portrait cutout inference
Mar 26, 2024 pm 01:00 PM
Overview In order to enable ModelScope users to quickly and conveniently use various models provided by the platform, a set of fully functional Python libraries are provided, which includes the implementation of ModelScope official models, as well as the necessary tools for using these models for inference, finetune and other tasks. Code related to data pre-processing, post-processing, effect evaluation and other functions, while also providing a simple and easy-to-use API and rich usage examples. By calling the library, users can complete tasks such as model reasoning, training, and evaluation by writing just a few lines of code. They can also quickly perform secondary development on this basis to realize their own innovative ideas. The algorithm model currently provided by the library is:




