Differences and connections: AIC and bBIC
Jan 23, 2024 pm 11:03 PM
AIC (Akaike Information Criterion) and BIC (Bayesian Information Criterion) are commonly used model selection criteria for comparing different models and selecting the model that best fits the data. The goal of both criteria is to find a balance between the goodness of fit and complexity of the model to avoid overfitting or underfitting problems. AIC was proposed by Hirotugu Akaike. It is based on the concept of information theory and considers the balance between the goodness of fit of the model and the number of parameters. The calculation formula of AIC is AIC = -2log(L) 2k, where L represents the maximum likelihood estimate of the model and k represents the number of parameters of the model. BIC was proposed by Gideon E. Schwarz and is based on Bayesian
AIC and BIC are indicators used to weigh the fitness and complexity of the model and can be applied to various Statistical models, including clustering methods. However, the specific forms of AIC and BIC may differ due to different types of clustering methods and assumptions about data distribution.
The main difference between AIC and BIC is how they weigh the trade-off between goodness of fit and complexity.
AIC is based on the maximum likelihood principle, which penalizes models with a large number of parameters relative to the size of the data.
Formula of AIC
AIC=2k-2ln(L)
The goal is to find the model with the lowest AIC value to balance goodness of fit and complexity. where k is the number of model parameters, which is the maximum likelihood of model L.
BIC is similar to AIC, but it penalizes models with a larger number of parameters more severely.
BIC formula
BIC=kln(n)-2ln(L)
where k is the n number of parameters in the model, is the number of data points, and L is Maximum likelihood of the model. The goal is to find the model with the lowest BIC value, as this indicates that the model has the best balance of goodness of fit and complexity.
Generally speaking, BIC will penalize models with a large number of parameters more severely than AIC, so BIC can be used when the goal is to find a more parsimonious model.
In the context of model selection, a parsimonious model is a model that has a small number of parameters but still fits the data well. The goal of parsimonious models is to simplify the model and reduce complexity while still capturing the essential characteristics of the data. When providing similar levels of accuracy, parsimonious models are preferred over more complex models because it is easier to interpret, less prone to overfitting, and more computationally efficient.
It is also important to note that both AIC and BIC can be used to compare different models and choose the best model for a given data set.
The above is the detailed content of Differences and connections: AIC and bBIC. For more information, please follow other related articles on the PHP Chinese website!

Hot Article

Hot tools Tags

Hot Article

Hot Article Tags

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
Jun 28, 2024 am 03:51 AM
Bytedance Cutting launches SVIP super membership: 499 yuan for continuous annual subscription, providing a variety of AI functions
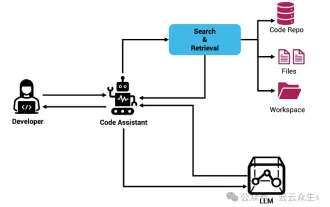 Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
Jun 10, 2024 am 11:08 AM
Context-augmented AI coding assistant using Rag and Sem-Rag
 Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
Jun 07, 2024 am 10:06 AM
Seven Cool GenAI & LLM Technical Interview Questions
 Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
Jun 11, 2024 pm 03:57 PM
Can fine-tuning really allow LLM to learn new things: introducing new knowledge may make the model produce more hallucinations
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
 SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
Jul 17, 2024 pm 06:37 PM
SOTA performance, Xiamen multi-modal protein-ligand affinity prediction AI method, combines molecular surface information for the first time
 Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
Jun 05, 2024 pm 08:51 PM
Five schools of machine learning you don't know about
 SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.
Aug 01, 2024 pm 09:40 PM
SK Hynix will display new AI-related products on August 6: 12-layer HBM3E, 321-high NAND, etc.







