ICLR 2024 | The first zero-order optimized deep learning framework, MSU and LLNL propose DeepZero

This article is a study on improving the scalability of zero-order optimization. The code has been open source and the paper has been accepted by ICLR 2024.

Today I’d like to introduce a paper titled “DeepZero: Scaling up Zeroth-Order Optimization for Deep Model Training” by Michigan State University and Lawrence Livermore National Laboratory collaboration is completed. This paper was recently accepted by the ICLR 2024 conference, and the research team has made the code open source. The main goal of this paper is to extend zero-order optimization techniques in deep learning model training. Zero-order optimization is an optimization method that does not rely on gradient information and can better handle high-dimensional parameter spaces and complex model structures. However, existing zero-order optimization methods face scale and efficiency challenges when dealing with deep learning models. To address these challenges, the research team proposed the DeepZero framework. This framework can efficiently handle the training of large-scale deep learning models by introducing new sampling strategies and adaptive adjustment mechanisms. DeepZero takes advantage of zero-order optimization and combines distributed computing and parallelization techniques to accelerate training over

• Paper address: https://arxiv.org/abs/2310.02025

• Project address: https://www.optml-group.com/posts/deepzero_iclr24

1. Background

Zeroth-Order (ZO) optimization has become a popular technology to solve machine learning (Machine Learning) problems, especially It is when the first-order (FO) information is difficult or impossible to obtain:

• Physics and chemistry and other disciplines: Machine learning models may be related to Complex simulator or experimental interactions where the underlying system is not differentiable.

• Black box learning scenario: When a deep learning (Deep Learning) model is integrated with a third-party API, such as adversarial attacks against the black box deep learning model and Defense, and black-box prompt learning of language model services.

• Hardware limitations: The principle backpropagation mechanism used to calculate first-order gradients may not be supported when implementing deep learning models on hardware systems .

However, currently the scalability of zero-order optimization remains an unsolved problem: its use is mainly limited to relatively small-scale machine learning problems, such as sample-level adversarial attacks. generate. As the dimensionality of the problem increases, the accuracy and efficiency of traditional zero-order methods decrease. This is because the gradient estimate based on zero-order finite difference is a biased estimate of the first-order gradient, and the deviation is more obvious in high-dimensional space. These challenges motivate the core question discussed in this article: How to extend zero-order optimization so that it can train deep learning models?

2. Zero-order gradient estimation: RGE or CGE?

The zero-order optimizer interacts with the objective function only by submitting inputs and receiving corresponding function values. There are two main gradient estimation methods: Coordinate Gradient Estimation (CGE) and Random Gradient Estimation (RGE), as shown below:

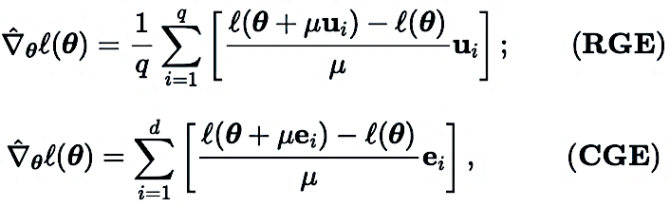
where 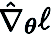represents an estimate of the first-order gradient of the optimization variable 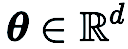(e.g., model parameters of a neural network).

In (RGE), 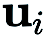represents a random perturbation vector, for example, drawn from a standard Gaussian distribution; 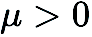is the perturbation size (also known as smoothing parameter); q is used to obtain the finite difference Number of random directions.

В (CGE) 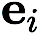представляет стандартный базисный вектор, 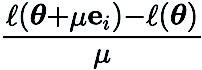обеспечивает оценку конечной разности частной производной 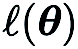в соответствующих координатах.

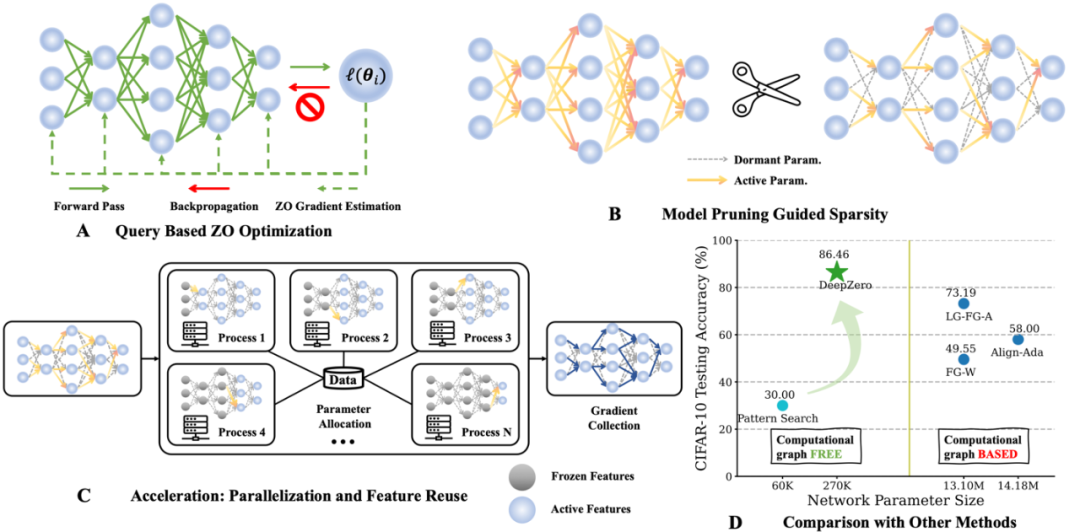
По сравнению с CGE, RGE позволяет сократить количество вычислений функций. Несмотря на высокую эффективность запросов, до сих пор неясно, сможет ли RGE обеспечить удовлетворительную точность при обучении глубоких моделей с нуля. С этой целью мы провели исследование, в ходе которого обучили небольшие сверточные нейронные сети (CNN) разного размера на CIFAR-10 с использованием RGE и CGE. Как показано на рисунке ниже, CGE может достичь точности тестирования, сравнимой с обучением оптимизации первого порядка, и значительно лучше, чем RGE, а также более эффективен по времени, чем RGE.

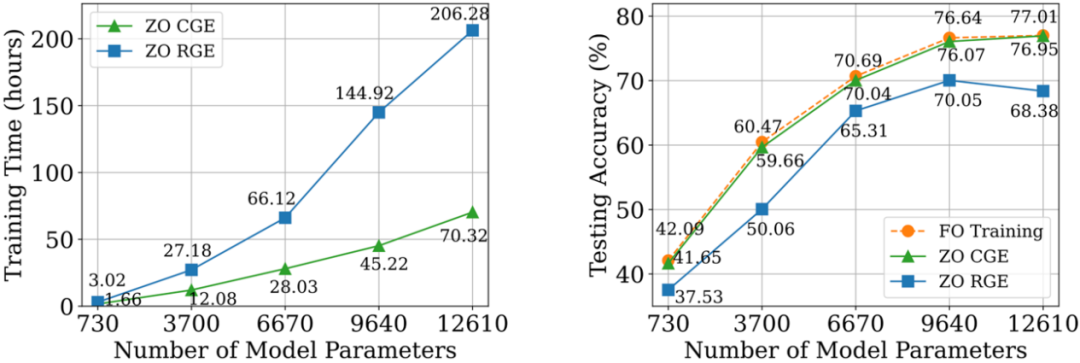
Основываясь на преимуществах CGE перед RGE с точки зрения точности и вычислительной эффективности, Мы выбираем CGE в качестве предпочтительного средства оценки градиента нулевого порядка. Однако сложность запросов CGE остается узким местом, поскольку она масштабируется с размером модели.

3. Фреймворк глубокого обучения нулевого порядка: DeepZero

Насколько нам известно, предыдущая работа не показала, что оптимизация ZO не эффективна при обучении глубоких нейронов сетей (DNN) Может существенно снизить эффективность работы. Чтобы преодолеть это препятствие, мы разработали DeepZero, принципиальную структуру глубокого обучения для оптимизации нулевого порядка, которая может расширить оптимизацию нулевого порядка до обучения нейронных сетей с нуля.

a) Отсечение модели нулевого порядка (ZO-GraSP): случайно инициализированная плотная нейронная сеть часто содержит высококачественную разреженную подсеть. Однако наиболее эффективные методы сокращения включают обучение модели в качестве промежуточного этапа. Следовательно, они не подходят для поиска разреженности посредством оптимизации нулевого порядка. Для решения вышеуказанных проблем нас вдохновил метод сокращения без обучения, называемый сокращением инициализации. Среди таких методов было выбрано сохранение градиентного сигнала (GraSP), которое представляет собой метод определения априорной разреженности нейронных сетей путем случайной инициализации градиентного потока сети.

b) Разреженный градиент: Чтобы сохранить преимущества точности обучения плотных моделей, в CGE мы включаем разреженность градиента вместо разреженности веса. Это гарантирует, что мы обучаем плотную модель в весовом пространстве, а не разреженную модель. В частности, мы используем ZO-GraSP для определения послойных коэффициентов сокращения (LPR), которые могут отражать сжимаемость DNN, а затем оптимизация нулевого порядка может обучаться плотно путем непрерывного итеративного обновления весов некоторых параметров модели. коэффициент градиента определяется LPR. c)

Повторное использование функций

: Поскольку CGE искажает каждый параметр поэлементно, он может повторно использовать функции непосредственно перед слоем возмущения и вместо этого выполнять оставшиеся операции прямого распространения начиная с входного слоя. Эмпирически, CGE с повторным использованием функций может сократить время обучения более чем в 2 раза. d)

Первый проход

: CGE поддерживает распараллеливание обучения модели. Это свойство развязки позволяет масштабировать прямое распространение между распределенными машинами, значительно увеличивая скорость обучения нулевого порядка.

4.Экспериментальный анализ

а) Классификация изображений

На наборе данных CIFAR-10 обучаем DeepZero ResNet -20 сравнивается с двумя вариантами, обученными с помощью оптимизации первого порядка:

(1) Dense ResNet-20, обученный с помощью оптимизации первого порядка

(2) Dense ResNet-20, полученный первым - оптимизация порядка Оптимизированное обучение разреженного ResNet-20

, полученного с помощью FO-GraSP, показано на рисунке ниже. Хотя в интервале разреженности от 80% до 99%, по сравнению с (1), модель, обученная с помощью DeepZero по-прежнему точный градусный разрыв. Это подчеркивает проблемы оптимизации ZO для глубокого обучения моделей, где желательны реализации с высокой разреженностью. Стоит отметить, что DeepZero превосходит (2) в интервале разрежённости от 90% до 99%,

демонстрируя превосходство разрежённости градиента над разрежённостью веса в DeepZero

.

б) Защита от черного ящика

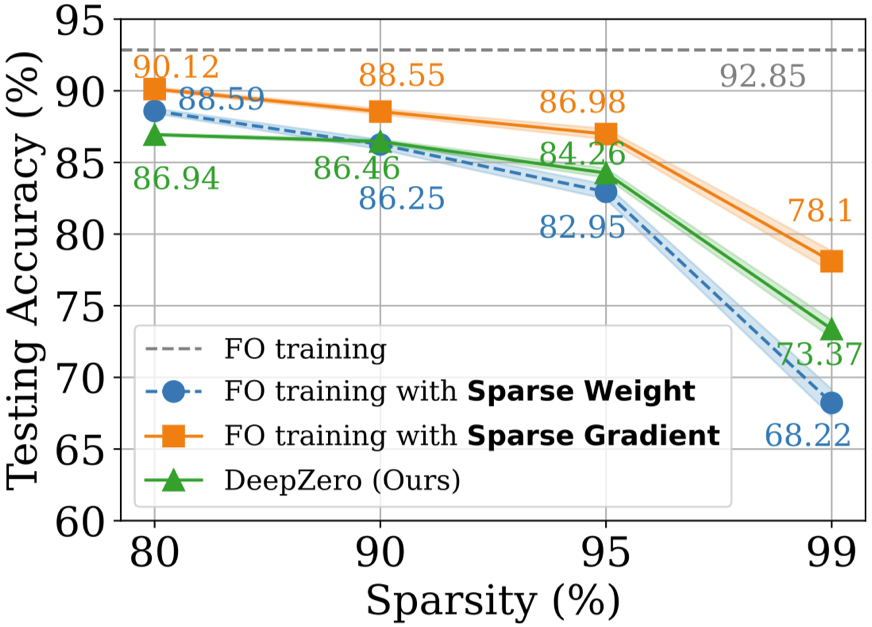
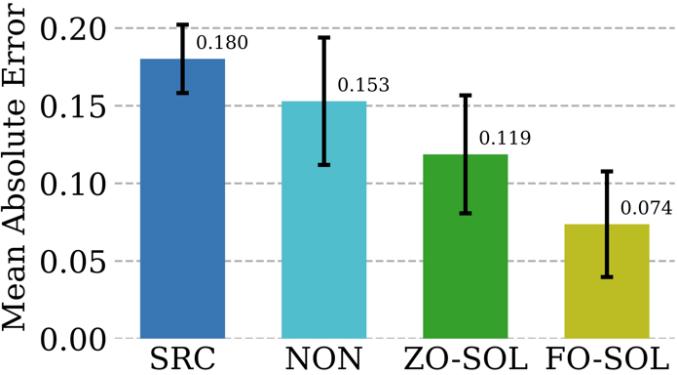
Проблема защиты «черного ящика» возникает, когда владелец модели не желает делиться деталями модели с защитником. Это создает проблему для существующих алгоритмов повышения надежности, которые напрямую улучшают модели белого ящика с использованием обучения оптимизации первого порядка. Чтобы преодолеть эту проблему, предлагается ZO-AE-DS, который вводит автоэнкодер (AE) между защитной операцией сглаживания шума белого ящика (DS) и классификатором изображений черного ящика для решения задач обучения ZO Dimensional. ZO-AE-DS имеет тот недостаток, что его трудно масштабировать до наборов данных с высоким разрешением (например, ImageNet), поскольку использование AE ставит под угрозу точность изображений, вводимых в классификатор изображений черного ящика, и приводит к снижению производительности защиты. Напротив, DeepZero может напрямую изучать защитные операции , интегрированные с классификатором черного ящика, без необходимости использования автокодировщика. Как показано в таблице ниже, DeepZero неизменно превосходит ZO-AE-DS по всем входным радиусам возмущений с точки зрения сертифицированной точности (CA).

#c) Глубокое обучение в сочетании с моделированием

Численные методы незаменимы при моделировании физической информации, но они сами существуют Есть проблемы: дискретизация неизбежно приводит к числовым ошибкам. Возможность исправления нейронных сетей посредством циклического интерактивного обучения с помощью итеративного решателя уравнений в частных производных (PDE) называется решателем в цикле (SOL). В то время как существующая работа сосредоточена на использовании или разработке дифференцируемых симуляторов для обучения моделей, мы расширяем SOL, используя DeepZero, чтобы обеспечить возможность использования с недифференцируемыми симуляторами или симуляторами черного ящика. В следующей таблице сравниваются характеристики исправления ошибок теста ZO-SOL (реализованного DeepZero) с тремя различными дифференцируемыми методами:

(1) SRC (моделирование с низкой точностью без исправления ошибок);

(2) NON (неинтерактивное обучение, выполняемое вне цикла моделирования с использованием предварительно сгенерированных данных моделирования с низкой и высокой точностью);

(3) FO-SOL (с учетом дифференцируемого времени моделирования, используется для обучения SOL первого порядка).

Ошибка для каждого тестового моделирования рассчитывается как средняя абсолютная ошибка (MAE) скорректированного моделирования по сравнению с высокоточным моделированием. Результаты показывают, что ZO-SOL, реализованный через DeepZero, по-прежнему превосходит SRC и NON и устраняет разрыв в производительности с FO-SOL даже при доступе только к симулятору на основе запросов. Производительность ZO-SOL по сравнению с NON подчеркивает перспективность ZO-SOL при интеграции симулятора черного ящика.

#####################################################) В этом документе представлена ​​структура глубокого обучения оптимизации нулевого порядка (DeepZero) для глубокого обучения сети. ). В частности, DeepZero объединяет оценку градиента координат, разреженность градиента, возникающую за счет сокращения модели нулевого порядка, повторное использование функций и распараллеливание переднего прохода в единый процесс обучения. Используя эти инновации, DeepZero продемонстрировал эффективность и результативность в решении задач, включая классификацию изображений и различные практические сценарии глубокого обучения «черный ящик». Кроме того, исследуется применимость DeepZero в других областях, таких как приложения, включающие недифференцируемые физические объекты, и обучение на устройствах, где не поддерживаются вычислительные графики и вычисления обратного распространения ошибки. #########Знакомство с автором#########Чжан Имэн, аспирантка в области компьютерных наук в лаборатории OPTML Мичиганского государственного университета, ее исследовательские интересы включают генеративный искусственный интеллект, мультимодальность. , Компьютерное зрение, Безопасный ИИ, Эффективный ИИ. ###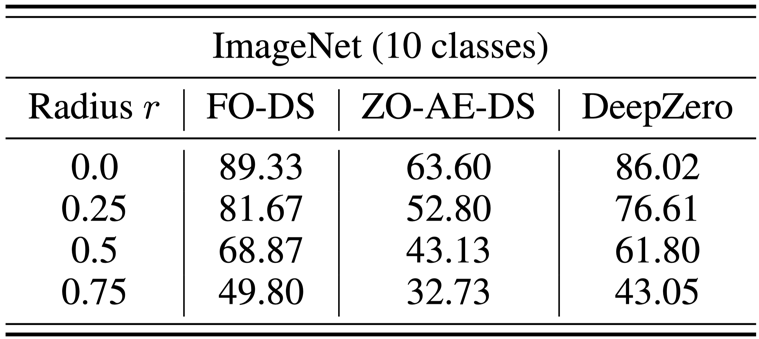

The above is the detailed content of ICLR 2024 | The first zero-order optimized deep learning framework, MSU and LLNL propose DeepZero. For more information, please follow other related articles on the PHP Chinese website!