 Technology peripherals
Technology peripherals
 AI
AI
 Teach you step by step how to implement a sparse mixed expert architecture language model (MoE) from scratch
Teach you step by step how to implement a sparse mixed expert architecture language model (MoE) from scratch
Teach you step by step how to implement a sparse mixed expert architecture language model (MoE) from scratch
This article introduces the method of implementing a sparse mixed expert language model (MoE), and explains the implementation process of the model in detail, including using sparse mixed experts to replace the traditional feedforwardNeural network, to achieve Top-k gating and top-k gating with noise, and using Kaiming He initialization technique. The authors also illustrate elements that remain unchanged from the makemore architecture, such as dataset processing, tokenization preprocessing, and language modeling tasks. Finally, a GitHub repository link is provided for the entire process of implementing the model. It is a rare practical textbook.
Introduction
Mixed expert models (MoE) began to receive widespread attention after their release, especially in sparse mixed expert language models. Although most components are similar to traditional transformers, there are some issues with the training stability of sparse mixed expert language models, despite appearing relatively simple.
This configurable small-scale sparse MoE implementation method was introduced in a blog on Hugging Face, which may be very helpful for researchers who want to quickly experiment with new methods. The blog also provides detailed code based on PyTorch, which can be found at this link: https://github.com/AviSoori1x/makeMoE/tree/main. Such small-scale implementations help researchers conduct rapid experiments in this field.
This website has compiled this for the benefit of readers.
This article makes several changes based on the makemore architecture:
Use sparse mixed experts instead of a separate feedforwardNeural network;
Top-k gating and noisy Top-k gating;
Parameter initialization uses the Kaiming He initialization method, but this article The key point is the customizable initialization method, including the selection of initialization methods such as Xavier/Glorot.
At the same time, the following modules are consistent with makemore:
Dataset, preprocessing (word segmentation) part, and Andrej’s original choice of language modeling Task - Generate text content in the style of Shakespeare
Casusal self-attention mechanism
Training loop
InferenceLogic
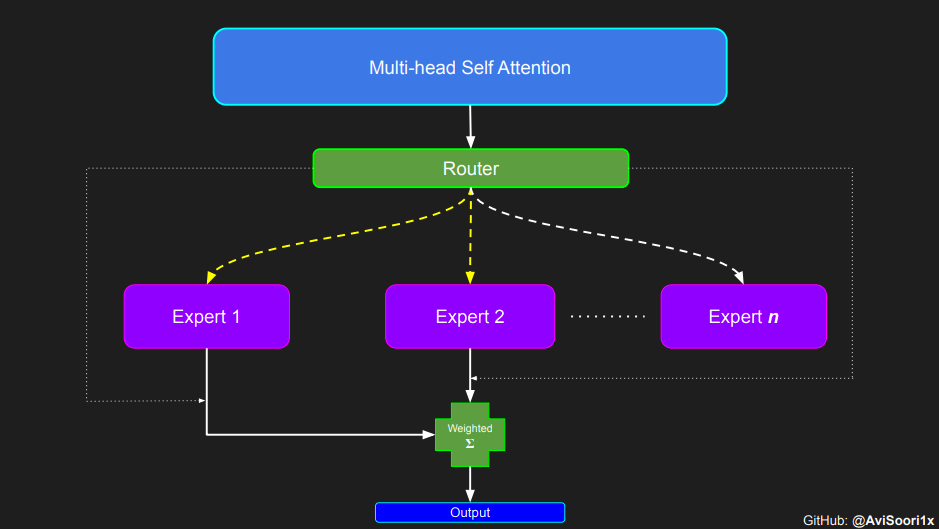
The implementation plan will be introduced step by step, starting with the attention mechanism.
Causal scaling dot product attention mechanism
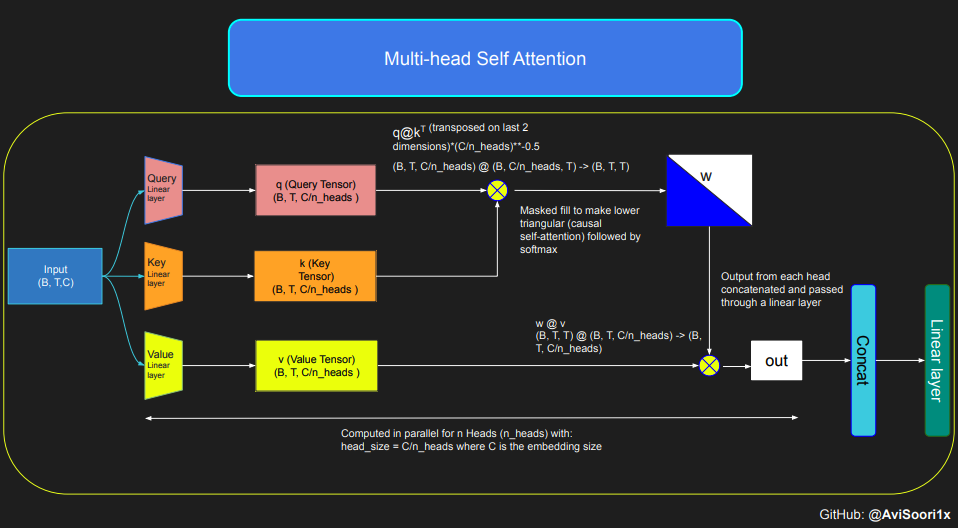
The following code shows the basic concept of the self-attention mechanism, and focuses on It is implemented using the classic scaled dot product self-attention. In this variant of self-attention, the query matrix, key matrix, and value matrix all come from the same input sequence. At the same time, in order to ensure the integrity of the autoregressive language generation process, especially in pure decoder models, a masking mechanism is used.
This masking mechanism is very critical because it can mask any information after the current token position, thereby guiding the model to only focus on the previous part of the sequence. This kind of attention that blocks the content behind the token is called causal self-attention. It is worth noting that the sparse mixed expert model is not limited to the decoder-only Transformer architecture. In fact, many important results in this field are centered around the T5 architecture, which also includes the encoder and decoder components in the Transformer model.
#This code is borrowed from Andrej Karpathy's makemore repository linked in the repo.The self attention layers in Sparse mixture of experts models are the same asin regular transformer modelstorch.manual_seed(1337)B,T,C = 4,8,32 # batch, time, channelsx = torch.randn(B,T,C)# let's see a single Head perform self-attentionhead_size = 16key = nn.Linear(C, head_size, bias=False)query = nn.Linear(C, head_size, bias=False)value = nn.Linear(C, head_size, bias=False)k = key(x) # (B, T, 16)q = query(x) # (B, T, 16)wei =q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)tril = torch.tril(torch.ones(T, T))#wei = torch.zeros((T,T))wei = wei.masked_fill(tril == 0, float('-inf'))wei = F.softmax(wei, dim=-1) #B,T,Tv = value(x) #B,T,Hout = wei @ v # (B,T,T) @ (B,T,H) -> (B,T,H)out.shape
torch.Size([4, 8, 16])
Then, the codes of causal self-attention and multi-head causal self-attention can be organized as follows. Multi-head self-attention applies multiple attention heads in parallel, with each attention head focusing solely on a part of the channel (embedding dimension). Multi-head self-attention essentially improves the learning process and increases the efficiency of model training due to its inherent parallel capabilities. The following code uses dropout for regularization to prevent overfitting.
#Causal scaled dot product self-Attention Headn_embd = 64n_head = 4n_layer = 4head_size = 16dropout = 0.1class Head(nn.Module):""" one head of self-attention """def __init__(self, head_size):super().__init__()self.key = nn.Linear(n_embd, head_size, bias=False)self.query = nn.Linear(n_embd, head_size, bias=False)self.value = nn.Linear(n_embd, head_size, bias=False)self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))self.dropout = nn.Dropout(dropout)def forward(self, x):B,T,C = x.shapek = self.key(x) # (B,T,C)q = self.query(x) # (B,T,C)# compute attention scores ("affinities")wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)wei = F.softmax(wei, dim=-1) # (B, T, T)wei = self.dropout(wei)# perform the weighted aggregation of the valuesv = self.value(x) # (B,T,C)out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C) return outThe implementation of multi-head self-attention is as follows:
#Multi-Headed Self Attentionclass MultiHeadAttention(nn.Module):""" multiple heads of self-attention in parallel """def __init__(self, num_heads, head_size):super().__init__()self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])self.proj = nn.Linear(n_embd, n_embd)self.dropout = nn.Dropout(dropout)def forward(self, x):out = torch.cat([h(x) for h in self.heads], dim=-1)out = self.dropout(self.proj(out)) return out
Create an expert module
That is, a simple multi-layer perceptron
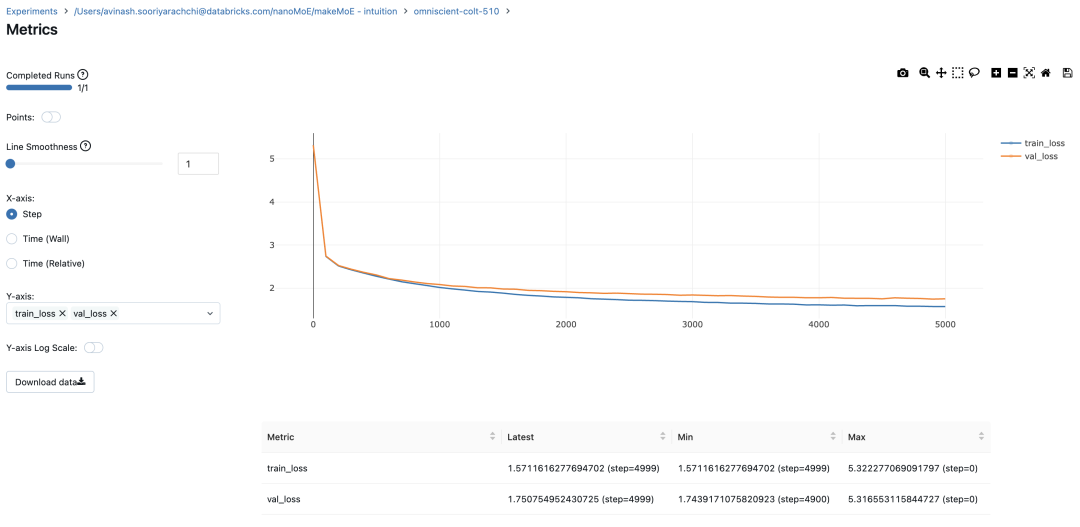
In the sparse mixed expert architecture, the self-attention mechanism within each transformer block remains unchanged. However, the structure of each block changes dramatically: the standard feedforward neural network is replaced by multiple sparsely activated feedforward networks (i.e. expert networks). The so-called "sparse activation" means that each token in the sequence is only assigned to a limited number of experts (usually one or two). 这有助于提高训练和推理速度,因为每次前向传递都会激活少数专家。不过,所有专家都必须存在 GPU 内存中,因此当参数总数达到数千亿甚至数万亿时,就会产生部署方面的问题。 Top-k 门控的一个例子 门控网络,也称为路由,确定哪个专家网络接收来自多头注意力的 token 的输出。举个例子解释路由的机制,假设有 4 个专家,token 需要被路由到前 2 个专家中。首先需要通过线性层将 token 输入到门控网络中。该层将对应于(Batch size,Tokens,n_embed)的输入张量从(2,4,32)维度,投影到对应于(Batch size、Tokens,num_expert)的新形状:(2、4,4)。其中 n_embed 是输入的通道维度,num_experts 是专家网络的计数。 接下来,沿最后一个维度,找出最大的前两个值及其相应的索引。 通过仅保留沿最后一个维度进行比较的前 k 大的值,来获得稀疏门控的输出。用负无穷值填充其余部分,在使用 softmax 激活函数。负无穷会被映射至零,而最大的前两个值会更加突出,且和为 1。要求和为 1 是为了对专家输出的内容进行加权。 使用有噪声的 top-k 门控以实现负载平衡 接下来使用下面这段代码来测试程序: 尽管最近发布的 mixtral 的论文没有提到这一点,但本文的作者相信有噪声的 Top-k 门控机制是训练 MoE 模型的一个重要工具。从本质上讲,不会希望所有的 token 都发送给同一组「受欢迎」的专家网络。人们需要的是能在开发和探索之间取得良好平衡。为此,为了负载平衡,从门控的线性层向 logits 激活函数添加标准正态噪声是有帮助的,这使训练更有效率。 再次尝试代码: 创建稀疏化的混合专家模块 在获得门控网络的输出结果之后,对于给定的 token,将前 k 个值选择性地与来自相应的前 k 个专家的输出相乘。这种选择性乘法的结果是一个加权和,该加权和构成 SparseMoe 模块的输出。这个过程的关键和难点是避免不必要的乘法运算,只为前 k 名专家进行正向转播。为每个专家执行前向传播将破坏使用稀疏 MoE 的目的,因为这个过程将不再是稀疏的。 运行以下代码来用样本测试上述实现,可以看到确实如此! 需要强调的是,如上代码所示,从路由 / 门控网络输出的 top_k 本身也很重要。索引确定了被激活的专家是哪些, 对应的值又决定了权重大小。下图进一步解释了加权求和的概念。 模块整合 将多头自注意力和稀疏混合专家相结合,形成稀疏混合专家 transformer 块。就像在 vanilla transformer 块中一样,也要使用残差以确保训练稳定,并避免梯度消失等问题。此外,要采用层归一化来进一步稳定学习过程。 最后,将所有内容整合在一起,形成稀疏混合专家语言模型。 参数初始化对于深度神经网络的高效训练非常重要。由于专家中存在 ReLU 激活,因此这里使用了 Kaiming He 初始化。也可以尝试在 transformer 中更常用的 Glorot 初始化。杰里米 - 霍华德(Jeremy Howard)的《Fastai》第 2 部分有一个从头开始实现这些功能的精彩讲座:https://course.fast.ai/Lessons/lesson17.html Glorot 参数初始化通常被用于 transformer 模型,因此这是一个可能提高模型性能的方法。 本文作者使用 mlflow 跟踪并记录重要指标和训练超参数。 记录训练和验证损失可以很好地指示训练的进展情况。该图显示,可能应该在 4500 次时停止(当验证损失稍微增加时) 接下来可以使用这个模型逐字符自回归地生成文本。 本文参考内容: 在实施过程中,作者大量参考了以下出版物: 混合专家模型:https://arxiv.org/pdf/2401.04088.pdf 超大型神经网络:稀疏门控混合专家层:https://arxiv.org/pdf/1701.06538.pdf 来自 Andrej Karpathy 的原始 makemore 实现:https://github.com/karpathy/makemore 还可以尝试以下几种方法,来提高模型性能: 提高混合专家模块的效率; 尝试不同的神经网络初始化策略; 从字符级到子词级的分词; 对专家数量和 k 的取值(每个 token 激活的专家数量)进行贝叶斯超参数搜索。这可以归类为神经架构搜索。 优化专家能力。 The above is the detailed content of Teach you step by step how to implement a sparse mixed expert architecture language model (MoE) from scratch. For more information, please follow other related articles on the PHP Chinese website!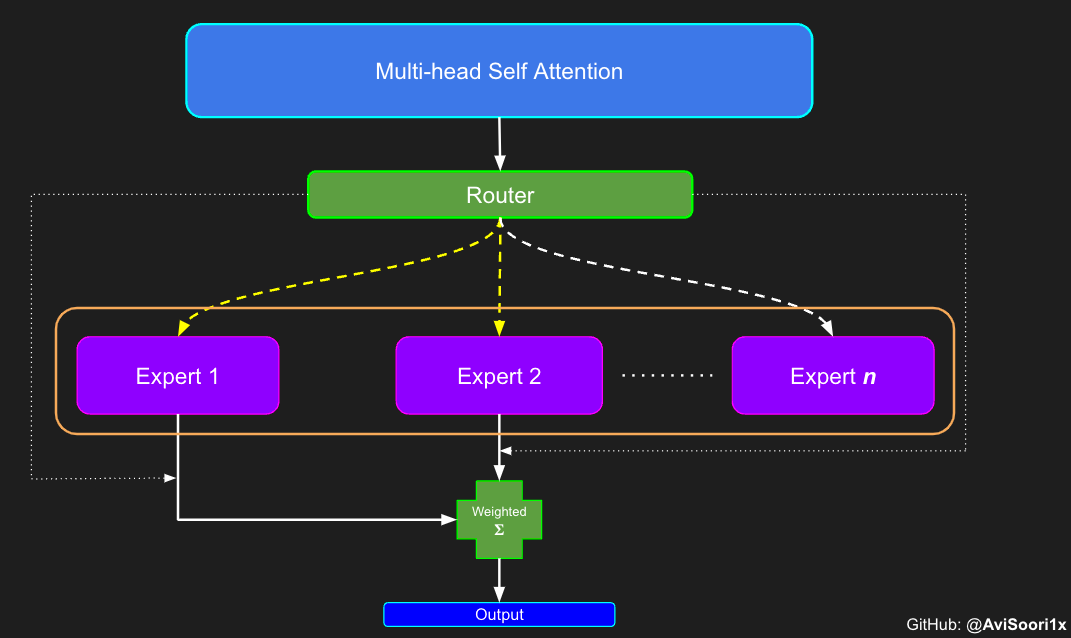
#Expert moduleclass Expert(nn.Module):""" An MLP is a simple linear layer followed by a non-linearity i.e. each Expert """def __init__(self, n_embd):super().__init__()self.net = nn.Sequential(nn.Linear(n_embd, 4 * n_embd),nn.ReLU(),nn.Linear(4 * n_embd, n_embd),nn.Dropout(dropout),)def forward(self, x): return self.net(x)
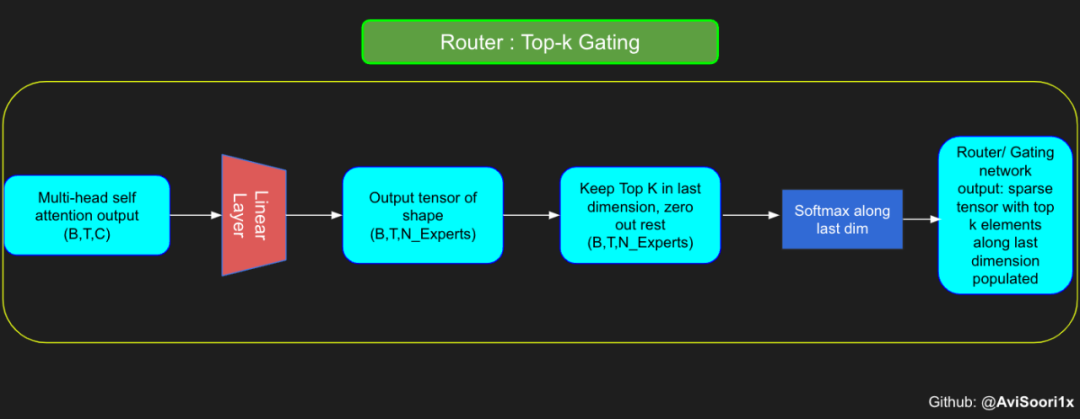
#Understanding how gating worksnum_experts = 4top_k=2n_embed=32#Example multi-head attention output for a simple illustrative example, consider n_embed=32, context_length=4 and batch_size=2mh_output = torch.randn(2, 4, n_embed)topkgate_linear = nn.Linear(n_embed, num_experts) # nn.Linear(32, 4)logits = topkgate_linear(mh_output)top_k_logits, top_k_indices = logits.topk(top_k, dim=-1)# Get top-k expertstop_k_logits, top_k_indices
#output:(tensor([[[ 0.0246, -0.0190],[ 0.1991,0.1513],[ 0.9749,0.7185],[ 0.4406, -0.8357]], [[ 0.6206, -0.0503],[ 0.8635,0.3784],[ 0.6828,0.5972],[ 0.4743,0.3420]]], grad_fn=<TopkBackward0>), tensor([[[2, 3],[2, 1],[3, 1],[2, 1]], [[0, 2], [0, 3], [3, 2], [3, 0]]]))
zeros = torch.full_like(logits, float('-inf')) #full_like clones a tensor and fills it with a specified value (like infinity) for masking or calculations.sparse_logits = zeros.scatter(-1, top_k_indices, top_k_logits)sparse_logits
#outputtensor([[[ -inf,-inf,0.0246, -0.0190], [ -inf,0.1513,0.1991,-inf], [ -inf,0.7185,-inf,0.9749], [ -inf, -0.8357,0.4406,-inf]],[[ 0.6206,-inf, -0.0503,-inf], [ 0.8635,-inf,-inf,0.3784], [ -inf,-inf,0.5972,0.6828], [ 0.3420,-inf,-inf,0.4743]]], grad_fn=<ScatterBackward0>)
gating_output= F.softmax(sparse_logits, dim=-1)gating_output
#ouputtensor([[[0.0000, 0.0000, 0.5109, 0.4891], [0.0000, 0.4881, 0.5119, 0.0000], [0.0000, 0.4362, 0.0000, 0.5638], [0.0000, 0.2182, 0.7818, 0.0000]],[[0.6617, 0.0000, 0.3383, 0.0000], [0.6190, 0.0000, 0.0000, 0.3810], [0.0000, 0.0000, 0.4786, 0.5214], [0.4670, 0.0000, 0.0000, 0.5330]]], grad_fn=<SoftmaxBackward0>)
# First define the top k router moduleclass TopkRouter(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(TopkRouter, self).__init__()self.top_k = top_kself.linear =nn.Linear(n_embed, num_experts) def forward(self, mh_ouput):# mh_ouput is the output tensor from multihead self attention blocklogits = self.linear(mh_output)top_k_logits, indices = logits.topk(self.top_k, dim=-1)zeros = torch.full_like(logits, float('-inf'))sparse_logits = zeros.scatter(-1, indices, top_k_logits)router_output = F.softmax(sparse_logits, dim=-1) return router_output, indices
#Testing this out:num_experts = 4top_k = 2n_embd = 32mh_output = torch.randn(2, 4, n_embd)# Example inputtop_k_gate = TopkRouter(n_embd, num_experts, top_k)gating_output, indices = top_k_gate(mh_output)gating_output.shape, gating_output, indices#And it works!!
#output(torch.Size([2, 4, 4]), tensor([[[0.5284, 0.0000, 0.4716, 0.0000],[0.0000, 0.4592, 0.0000, 0.5408],[0.0000, 0.3529, 0.0000, 0.6471],[0.3948, 0.0000, 0.0000, 0.6052]], [[0.0000, 0.5950, 0.4050, 0.0000], [0.4456, 0.0000, 0.5544, 0.0000], [0.7208, 0.0000, 0.0000, 0.2792], [0.0000, 0.0000, 0.5659, 0.4341]]], grad_fn=<SoftmaxBackward0>), tensor([[[0, 2],[3, 1],[3, 1],[3, 0]], [[1, 2], [2, 0], [0, 3], [2, 3]]]))
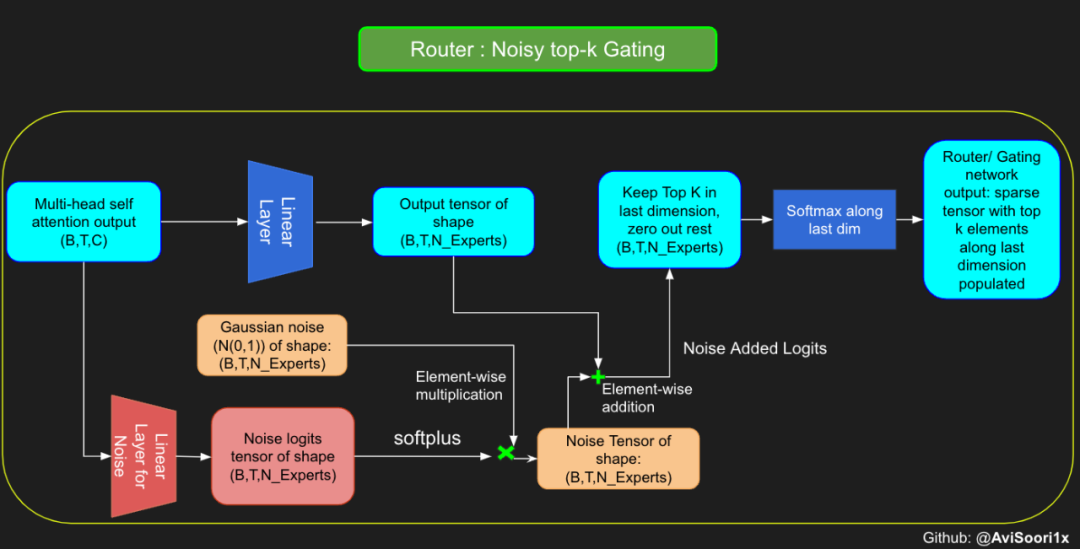
#Changing the above to accomodate noisy top-k gatingclass NoisyTopkRouter(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(NoisyTopkRouter, self).__init__()self.top_k = top_k#layer for router logitsself.topkroute_linear = nn.Linear(n_embed, num_experts)self.noise_linear =nn.Linear(n_embed, num_experts)def forward(self, mh_output):# mh_ouput is the output tensor from multihead self attention blocklogits = self.topkroute_linear(mh_output)#Noise logitsnoise_logits = self.noise_linear(mh_output)#Adding scaled unit gaussian noise to the logitsnoise = torch.randn_like(logits)*F.softplus(noise_logits)noisy_logits = logits + noisetop_k_logits, indices = noisy_logits.topk(self.top_k, dim=-1)zeros = torch.full_like(noisy_logits, float('-inf'))sparse_logits = zeros.scatter(-1, indices, top_k_logits)router_output = F.softmax(sparse_logits, dim=-1) return router_output, indices
#Testing this out, again:num_experts = 8top_k = 2n_embd = 16mh_output = torch.randn(2, 4, n_embd)# Example inputnoisy_top_k_gate = NoisyTopkRouter(n_embd, num_experts, top_k)gating_output, indices = noisy_top_k_gate(mh_output)gating_output.shape, gating_output, indices#It works!!
#output(torch.Size([2, 4, 8]), tensor([[[0.4181, 0.0000, 0.5819, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.4693, 0.5307, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.0000, 0.4985, 0.5015, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],[0.0000, 0.0000, 0.0000, 0.2641, 0.0000, 0.7359, 0.0000, 0.0000]], [[0.0000, 0.0000, 0.0000, 0.6301, 0.0000, 0.3699, 0.0000, 0.0000], [0.0000, 0.0000, 0.0000, 0.4766, 0.0000, 0.0000, 0.0000, 0.5234], [0.0000, 0.0000, 0.0000, 0.6815, 0.0000, 0.0000, 0.3185, 0.0000], [0.4482, 0.5518, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]], grad_fn=<SoftmaxBackward0>), tensor([[[2, 0],[1, 0],[2, 1],[5, 3]], [[3, 5], [7, 3], [3, 6], [1, 0]]]))
class SparseMoE(nn.Module):def __init__(self, n_embed, num_experts, top_k):super(SparseMoE, self).__init__()self.router = NoisyTopkRouter(n_embed, num_experts, top_k)self.experts = nn.ModuleList([Expert(n_embed) for _ in range(num_experts)])self.top_k = top_kdef forward(self, x):gating_output, indices = self.router(x)final_output = torch.zeros_like(x)# Reshape inputs for batch processingflat_x = x.view(-1, x.size(-1))flat_gating_output = gating_output.view(-1, gating_output.size(-1))# Process each expert in parallelfor i, expert in enumerate(self.experts):# Create a mask for the inputs where the current expert is in top-kexpert_mask = (indices == i).any(dim=-1)flat_mask = expert_mask.view(-1)if flat_mask.any():expert_input = flat_x[flat_mask]expert_output = expert(expert_input)# Extract and apply gating scoresgating_scores = flat_gating_output[flat_mask, i].unsqueeze(1)weighted_output = expert_output * gating_scores# Update final output additively by indexing and addingfinal_output[expert_mask] += weighted_output.squeeze(1) return final_output
import torchimport torch.nn as nn#Let's test this outnum_experts = 8top_k = 2n_embd = 16dropout=0.1mh_output = torch.randn(4, 8, n_embd)# Example multi-head attention outputsparse_moe = SparseMoE(n_embd, num_experts, top_k)final_output = sparse_moe(mh_output)print("Shape of the final output:", final_output.shape)Shape of the final output: torch.Size([4, 8, 16])
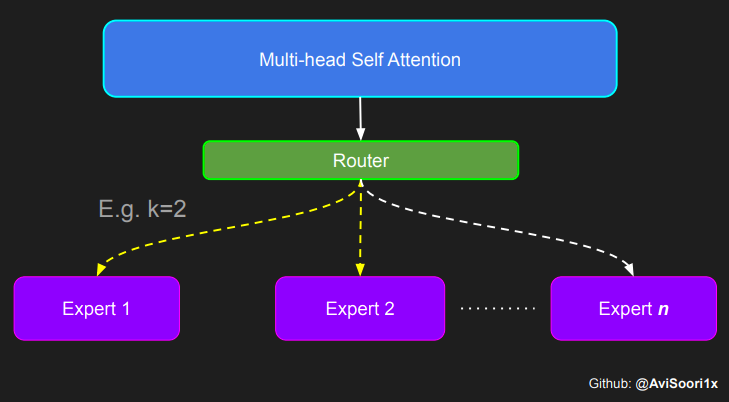
#Create a self attention + mixture of experts block, that may be repeated several number of timesclass Block(nn.Module):""" Mixture of Experts Transformer block: communication followed by computation (multi-head self attention + SparseMoE) """def __init__(self, n_embed, n_head, num_experts, top_k):# n_embed: embedding dimension, n_head: the number of heads we'd likesuper().__init__()head_size = n_embed // n_headself.sa = MultiHeadAttention(n_head, head_size)self.smoe = SparseMoE(n_embed, num_experts, top_k)self.ln1 = nn.LayerNorm(n_embed)self.ln2 = nn.LayerNorm(n_embed)def forward(self, x):x = x + self.sa(self.ln1(x))x = x + self.smoe(self.ln2(x)) return x
class SparseMoELanguageModel(nn.Module):def __init__(self):super().__init__()# each token directly reads off the logits for the next token from a lookup table self.token_embedding_table = nn.Embedding(vocab_size, n_embed) self.position_embedding_table = nn.Embedding(block_size, n_embed)self.blocks = nn.Sequential(*[Block(n_embed, n_head=n_head, num_experts=num_experts,top_k=top_k) for _ in range(n_layer)])self.ln_f = nn.LayerNorm(n_embed) # final layer normself.lm_head = nn.Linear(n_embed, vocab_size)def forward(self, idx, targets=None):B, T = idx.shape# idx and targets are both (B,T) tensor of integerstok_emb = self.token_embedding_table(idx) # (B,T,C)pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)x = tok_emb + pos_emb # (B,T,C)x = self.blocks(x) # (B,T,C)x = self.ln_f(x) # (B,T,C)logits = self.lm_head(x) # (B,T,vocab_size)if targets is None:loss = Noneelse:B, T, C = logits.shapelogits = logits.view(B*T, C)targets = targets.view(B*T)loss = F.cross_entropy(logits, targets)return logits, lossdef generate(self, idx, max_new_tokens):# idx is (B, T) array of indices in the current contextfor _ in range(max_new_tokens):# crop idx to the last block_size tokensidx_cond = idx[:, -block_size:]# get the predictionslogits, loss = self(idx_cond)# focus only on the last time steplogits = logits[:, -1, :] # becomes (B, C)# apply softmax to get probabilitiesprobs = F.softmax(logits, dim=-1) # (B, C)# sample from the distributionidx_next = torch.multinomial(probs, num_samples=1) # (B, 1)# append sampled index to the running sequenceidx = torch.cat((idx, idx_next), dim=1) # (B, T+1) return idx
def kaiming_init_weights(m):if isinstance (m, (nn.Linear)): init.kaiming_normal_(m.weight)model = SparseMoELanguageModel()model.apply(kaiming_init_weights)
#Using MLFlowm = model.to(device)# print the number of parameters in the modelprint(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')# create a PyTorch optimizeroptimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)#mlflow.set_experiment("makeMoE")with mlflow.start_run():#If you use mlflow.autolog() this will be automatically logged. I chose to explicitly log here for completenessparams = {"batch_size": batch_size , "block_size" : block_size, "max_iters": max_iters, "eval_interval": eval_interval,"learning_rate": learning_rate, "device": device, "eval_iters": eval_iters, "dropout" : dropout, "num_experts": num_experts, "top_k": top_k }mlflow.log_params(params)for iter in range(max_iters):# every once in a while evaluate the loss on train and val setsif iter % eval_interval == 0 or iter == max_iters - 1:losses = estimate_loss()print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")metrics = {"train_loss": losses['train'], "val_loss": losses['val']}mlflow.log_metrics(metrics, step=iter)# sample a batch of dataxb, yb = get_batch('train')# evaluate the losslogits, loss = model(xb, yb)optimizer.zero_grad(set_to_none=True)loss.backward()optimizer.step()8.996545 M parametersstep 0: train loss 5.3223, val loss 5.3166step 100: train loss 2.7351, val loss 2.7429step 200: train loss 2.5125, val loss 2.5233...step 4999: train loss 1.5712, val loss 1.7508
# generate from the model. Not great. Not too bad eithercontext = torch.zeros((1, 1), dtype=torch.long, device=device)print(decode(m.generate(context, max_new_tokens=2000)[0].tolist()))
DUKE VINCENVENTIO:If it ever fecond he town sue kigh now,That thou wold'st is steen 't.SIMNA:Angent her; no, my a born Yorthort,Romeoos soun and lawf to your sawe with ch a woft ttastly defy,To declay the soul art; and meart smad.CORPIOLLANUS:Which I cannot shall do from by born und ot cold warrike,What king we best anone wrave's going of heard and goodThus playvage; you have wold the grace....

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 A Diffusion Model Tutorial Worth Your Time, from Purdue University
Apr 07, 2024 am 09:01 AM
A Diffusion Model Tutorial Worth Your Time, from Purdue University
Apr 07, 2024 am 09:01 AM
Diffusion can not only imitate better, but also "create". The diffusion model (DiffusionModel) is an image generation model. Compared with the well-known algorithms such as GAN and VAE in the field of AI, the diffusion model takes a different approach. Its main idea is a process of first adding noise to the image and then gradually denoising it. How to denoise and restore the original image is the core part of the algorithm. The final algorithm is able to generate an image from a random noisy image. In recent years, the phenomenal growth of generative AI has enabled many exciting applications in text-to-image generation, video generation, and more. The basic principle behind these generative tools is the concept of diffusion, a special sampling mechanism that overcomes the limitations of previous methods.
 Generate PPT with one click! Kimi: Let the 'PPT migrant workers' become popular first
Aug 01, 2024 pm 03:28 PM
Generate PPT with one click! Kimi: Let the 'PPT migrant workers' become popular first
Aug 01, 2024 pm 03:28 PM
Kimi: In just one sentence, in just ten seconds, a PPT will be ready. PPT is so annoying! To hold a meeting, you need to have a PPT; to write a weekly report, you need to have a PPT; to make an investment, you need to show a PPT; even when you accuse someone of cheating, you have to send a PPT. College is more like studying a PPT major. You watch PPT in class and do PPT after class. Perhaps, when Dennis Austin invented PPT 37 years ago, he did not expect that one day PPT would become so widespread. Talking about our hard experience of making PPT brings tears to our eyes. "It took three months to make a PPT of more than 20 pages, and I revised it dozens of times. I felt like vomiting when I saw the PPT." "At my peak, I did five PPTs a day, and even my breathing was PPT." If you have an impromptu meeting, you should do it
 All CVPR 2024 awards announced! Nearly 10,000 people attended the conference offline, and a Chinese researcher from Google won the best paper award
Jun 20, 2024 pm 05:43 PM
All CVPR 2024 awards announced! Nearly 10,000 people attended the conference offline, and a Chinese researcher from Google won the best paper award
Jun 20, 2024 pm 05:43 PM
In the early morning of June 20th, Beijing time, CVPR2024, the top international computer vision conference held in Seattle, officially announced the best paper and other awards. This year, a total of 10 papers won awards, including 2 best papers and 2 best student papers. In addition, there were 2 best paper nominations and 4 best student paper nominations. The top conference in the field of computer vision (CV) is CVPR, which attracts a large number of research institutions and universities every year. According to statistics, a total of 11,532 papers were submitted this year, and 2,719 were accepted, with an acceptance rate of 23.6%. According to Georgia Institute of Technology’s statistical analysis of CVPR2024 data, from the perspective of research topics, the largest number of papers is image and video synthesis and generation (Imageandvideosyn
 PyCharm Community Edition Installation Guide: Quickly master all the steps
Jan 27, 2024 am 09:10 AM
PyCharm Community Edition Installation Guide: Quickly master all the steps
Jan 27, 2024 am 09:10 AM
Quick Start with PyCharm Community Edition: Detailed Installation Tutorial Full Analysis Introduction: PyCharm is a powerful Python integrated development environment (IDE) that provides a comprehensive set of tools to help developers write Python code more efficiently. This article will introduce in detail how to install PyCharm Community Edition and provide specific code examples to help beginners get started quickly. Step 1: Download and install PyCharm Community Edition To use PyCharm, you first need to download it from its official website
 From bare metal to a large model with 70 billion parameters, here is a tutorial and ready-to-use scripts
Jul 24, 2024 pm 08:13 PM
From bare metal to a large model with 70 billion parameters, here is a tutorial and ready-to-use scripts
Jul 24, 2024 pm 08:13 PM
We know that LLM is trained on large-scale computer clusters using massive data. This site has introduced many methods and technologies used to assist and improve the LLM training process. Today, what we want to share is an article that goes deep into the underlying technology and introduces how to turn a bunch of "bare metals" without even an operating system into a computer cluster for training LLM. This article comes from Imbue, an AI startup that strives to achieve general intelligence by understanding how machines think. Of course, turning a bunch of "bare metal" without an operating system into a computer cluster for training LLM is not an easy process, full of exploration and trial and error, but Imbue finally successfully trained an LLM with 70 billion parameters. and in the process accumulate
 Five programming software for getting started with learning C language
Feb 19, 2024 pm 04:51 PM
Five programming software for getting started with learning C language
Feb 19, 2024 pm 04:51 PM
As a widely used programming language, C language is one of the basic languages that must be learned for those who want to engage in computer programming. However, for beginners, learning a new programming language can be difficult, especially due to the lack of relevant learning tools and teaching materials. In this article, I will introduce five programming software to help beginners get started with C language and help you get started quickly. The first programming software was Code::Blocks. Code::Blocks is a free, open source integrated development environment (IDE) for
 AI in use | AI created a life vlog of a girl living alone, which received tens of thousands of likes in 3 days
Aug 07, 2024 pm 10:53 PM
AI in use | AI created a life vlog of a girl living alone, which received tens of thousands of likes in 3 days
Aug 07, 2024 pm 10:53 PM
Editor of the Machine Power Report: Yang Wen The wave of artificial intelligence represented by large models and AIGC has been quietly changing the way we live and work, but most people still don’t know how to use it. Therefore, we have launched the "AI in Use" column to introduce in detail how to use AI through intuitive, interesting and concise artificial intelligence use cases and stimulate everyone's thinking. We also welcome readers to submit innovative, hands-on use cases. Video link: https://mp.weixin.qq.com/s/2hX_i7li3RqdE4u016yGhQ Recently, the life vlog of a girl living alone became popular on Xiaohongshu. An illustration-style animation, coupled with a few healing words, can be easily picked up in just a few days.
 A must-read for technical beginners: Analysis of the difficulty levels of C language and Python
Mar 22, 2024 am 10:21 AM
A must-read for technical beginners: Analysis of the difficulty levels of C language and Python
Mar 22, 2024 am 10:21 AM
Title: A must-read for technical beginners: Difficulty analysis of C language and Python, requiring specific code examples In today's digital age, programming technology has become an increasingly important ability. Whether you want to work in fields such as software development, data analysis, artificial intelligence, or just learn programming out of interest, choosing a suitable programming language is the first step. Among many programming languages, C language and Python are two widely used programming languages, each with its own characteristics. This article will analyze the difficulty levels of C language and Python





