 Technology peripherals
Technology peripherals
 AI
AI
 Tsinghua University and Harbin Institute of Technology have compressed large models to 1 bit, and the desire to run large models on mobile phones is about to come true!
Tsinghua University and Harbin Institute of Technology have compressed large models to 1 bit, and the desire to run large models on mobile phones is about to come true!
Tsinghua University and Harbin Institute of Technology have compressed large models to 1 bit, and the desire to run large models on mobile phones is about to come true!
Mar 04, 2024 pm 02:31 PMSince large models became popular in the industry, people’s desire to compress large models has never diminished. This is because, although large models show excellent capabilities in many aspects, the high deployment cost greatly increases the threshold for its use. This cost mainly comes from space occupation and calculation amount. "Model quantization" saves space by converting the parameters of large models into low-bit-width representations. Currently, mainstream methods can compress existing models to 4 bits with almost no loss of model performance. However, quantization below 3 bits is like an insurmountable wall that daunts researchers.
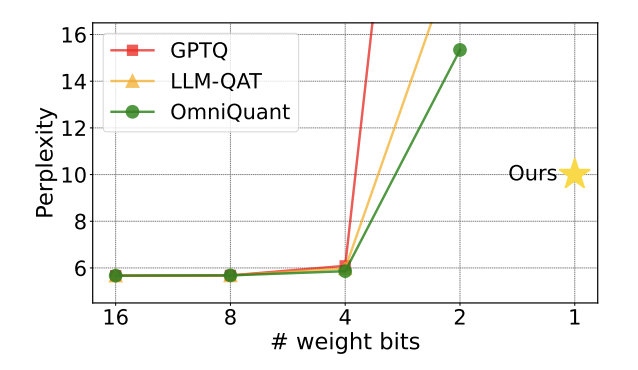
Figure 1: The perplexity of the quantitative model rises rapidly at 2 bit
Recently, an article The paper jointly published by Tsinghua University and Harbin Institute of Technology on arXiv brings hope to break through this obstacle and has attracted considerable attention in domestic and foreign academic circles. This paper was also listed as a hot paper on huggingface a week ago and was recommended by the famous paper recommender AK. The research team went directly beyond the 2-bit quantification level and boldly attempted 1-bit quantification. This was the first time in the research on model quantification.

Paper title: OneBit: Towards Extremely Low-bit Large Language Models
Paper address: https ://arxiv.org/pdf/2402.11295.pdf
The method proposed by the author is called "OneBit", which describes the essence of this work very aptly: Training large models is compressed to real 1bit. This paper proposes a new method of 1-bit representation of model parameters, as well as an initialization method for quantized model parameters, and migrates the capabilities of high-precision pre-trained models to 1-bit quantized models through quantization-aware training (QAT). Experiments show that this method can greatly compress the model parameters while ensuring at least 83% performance of the LLaMA model.
The author pointed out that when the model parameters are compressed to 1 bit, the "element multiplication" in matrix multiplication will no longer exist, and will be replaced by a faster "bit assignment" operation, which will Greatly improve computing efficiency. The importance of this research is that it not only crosses the 2-bit quantification gap, but also makes it possible to deploy large models on PCs and smartphones.
Limitations of existing work
Model quantification is mainly done by transforming the nn.Linear layer of the model (except the Embedding layer and Lm_head layer) Implementing spatial compression for low-precision representations. The basis of previous work [1,2] is to use the Round-To-Nearest (RTN) method to approximately map high-precision floating point numbers to a nearby integer grid. This can be expressed as 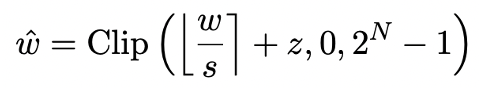 .
.
However, the method based on RTN has serious accuracy loss problem at extremely low bit width (below 3 bit), and the loss of model capability after quantization is very serious. In particular, when the quantized parameters are expressed in 1 bit, the scaling coefficient s and zero point z in RTN will lose their practical meaning. This causes the RTN-based quantization method to be almost ineffective at 1-bit quantization, making it difficult to effectively retain the performance of the original model.
In addition, previous research has also explored what structure the 1bit model may adopt. Work from a few months ago on BitNet [3] implements 1bit representation by passing model parameters through the Sign (・) function and converting to 1/-1. However, this method suffers from serious performance loss and unstable training process, which limits its practical application.
OneBit framework
OneBit’s method framework includes a new 1bit layer structure, a SVID-based parameter initialization method and a quantization-aware knowledge distillation-based Knowledge transfer.
1. New 1bit structure
The ultimate goal of OneBit is to convert LLMs The weight matrix is compressed to 1 bit. Real 1bit requires that each weight value can only be represented by 1bit, that is, there are only two possible states. The author believes that in the parameters of large models, two important factors must be taken into account, that is, the high precision of floating point numbers and the high rank of the parameter matrix.
Therefore, the author introduces two value vectors in FP16 format to compensate for the loss of accuracy due to quantization. This design not only maintains the high rank of the original weight matrix, but also provides the necessary floating point precision through the value vector, which facilitates model training and knowledge transfer. The comparison between the structure of 1bit linear layer and the structure of FP16 high-precision linear layer is as follows:
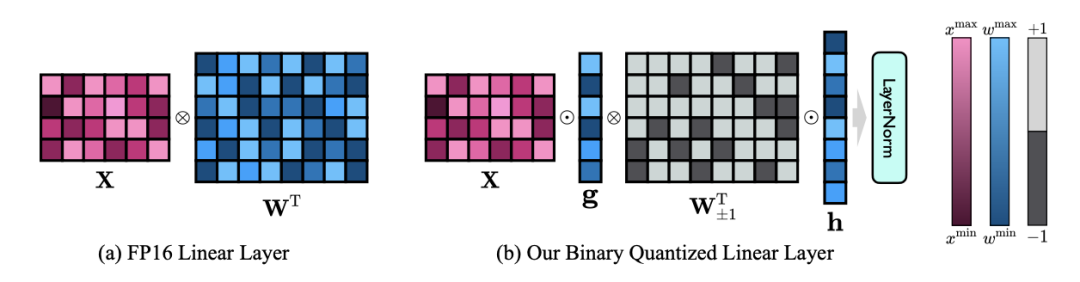
Figure 3: Comparison between FP16 linear layer and OneBit linear layer
(a) on the left is the FP16 precision model structure, and (b) on the right is the linear layer of the OneBit framework. It can be seen that in the OneBit framework, only the value vectors g and h remain in FP16 format, while the weight matrix is entirely composed of ±1. Such a structure takes into account both accuracy and rank, and is very meaningful for ensuring a stable and high-quality learning process.
How much does OneBit compress the model? The author gives a calculation in the paper. Assuming a 4096*4096 linear layer is compressed, OneBit requires a 4096*4096 1-bit matrix and two 4096*1 16-bit value vectors. The total number of bits is 16,908,288, and the total number of parameters is 16,785,408. On average, each parameter occupies only about 1.0073 bits. This kind of compression is unprecedented, and it can be said to be a truly 1-bit large model.
2. Initialize the quantization model based on SVID
In order to use the fully trained original model to better initialize the quantization The author proposes a new parameter matrix decomposition method called "value-sign independent matrix decomposition (SVID)". This matrix decomposition method separates symbols and absolute values, and performs rank-1 approximation on absolute values. Its approach to the original matrix parameters can be expressed as:
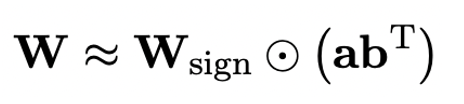
The rank-1 approximation here can be achieved through common matrix factorization methods, such as singular value decomposition (SVD) and nonnegative matrix factorization (NMF). Then, the author mathematically shows that this SVID method can match the 1-bit model framework by exchanging the order of operations, thereby achieving parameter initialization. Moreover, the paper also proves that the symbolic matrix does play a role in approximating the original matrix during the decomposition process.
3. Migrate the original model capabilities through knowledge distillation
The author pointed out that solving the problem of ultra-low bit width quantization of large models An effective way may be quantified perception training QAT. Under the OneBit model structure, knowledge distillation is used to learn from the unquantized model to realize the migration of capabilities to the quantized model. Specifically, the student model is mainly guided by the logits and hidden state of the teacher model.
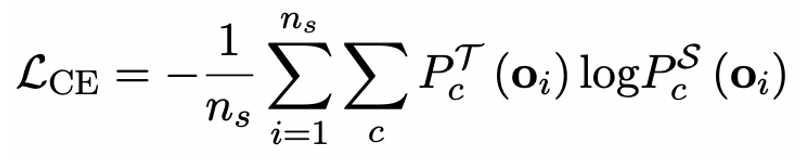
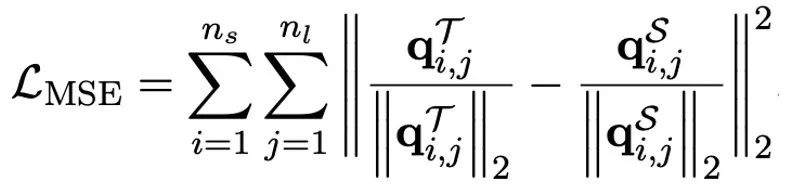
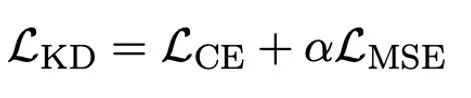
##During training, the values of the value vector and matrix will be updated. After the model quantification is completed, the parameters after Sign (・) are directly saved and used directly during inference and deployment.
Experiments and results
OneBit and FP16 Transformer, the classic post-training quantization strong baseline GPTQ, quantization-aware training strong baseline LLM-QAT and The latest 2-bit weight quantization strong baseline OmniQuant was compared. In addition, since there is currently no research on 1-bit weight quantization, the author only uses 1-bit weight quantization for his OneBit framework, and adopts 2-bit quantization settings for other methods, which is a typical "weak victory over the strong".
In terms of model selection, the author also selected models of different sizes from 1.3B to 13B, OPT and LLaMA-1/2 in different series to prove the effectiveness of OneBit. In terms of evaluation indicators, the author follows the two major evaluation dimensions of previous model quantification: the perplexity of the verification set and the zero-shot accuracy of common sense reasoning.
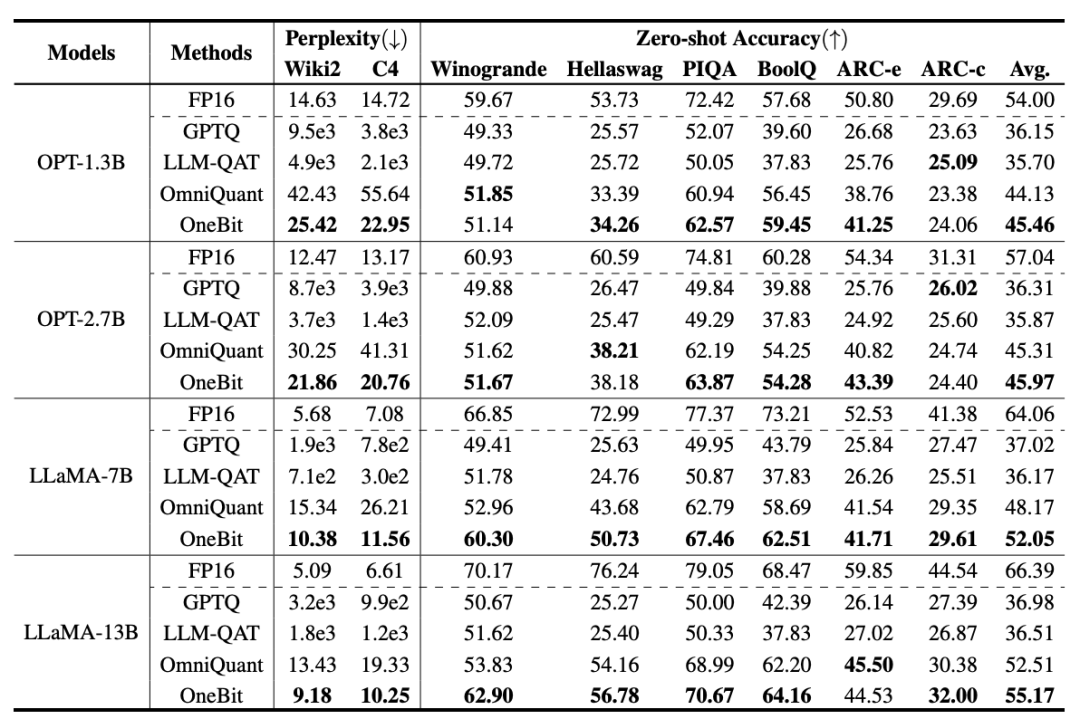
Table 1: Comparison of the effects of OneBit and baseline methods (OPT model and LLaMA-1 model)
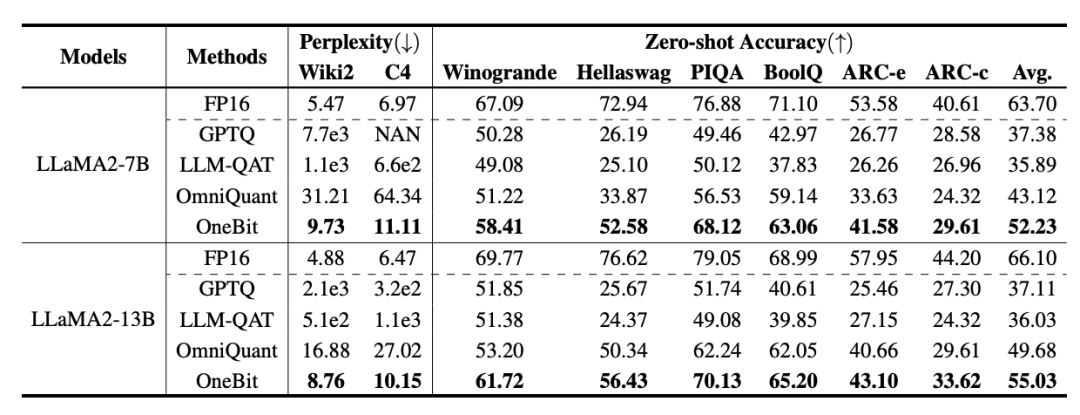
Table 2: Comparison of the effect of OneBit and baseline methods (LLaMA-2 model)
Table 1 and Table 2 show OneBit compared to other methods in 1-bit quantification time advantage. In terms of quantifying the perplexity of the model on the validation set, OneBit is closest to the FP16 model. In terms of zero-shot accuracy, the OneBit quantization model achieved almost the best performance except for the individual datasets of the OPT model. The remaining 2-bit quantization methods show larger losses on both evaluation metrics.
It is worth noting that OneBit tends to perform better when the model is larger. That is, as the model size increases, the FP16 precision model has little effect on perplexity reduction, but OneBit shows more perplexity reduction. In addition, the authors also point out that quantization-aware training may be necessary for ultra-low bitwidth quantization.
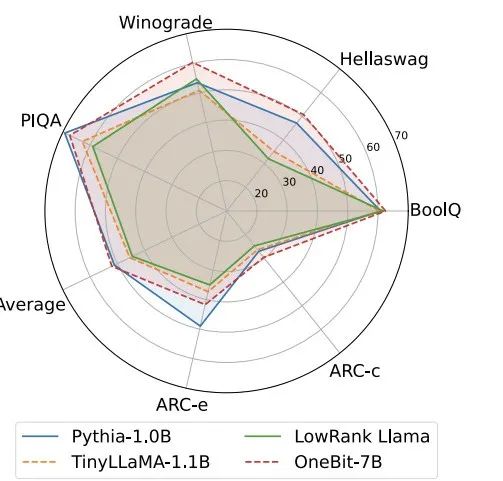
Figure 4: Common sense reasoning task comparison
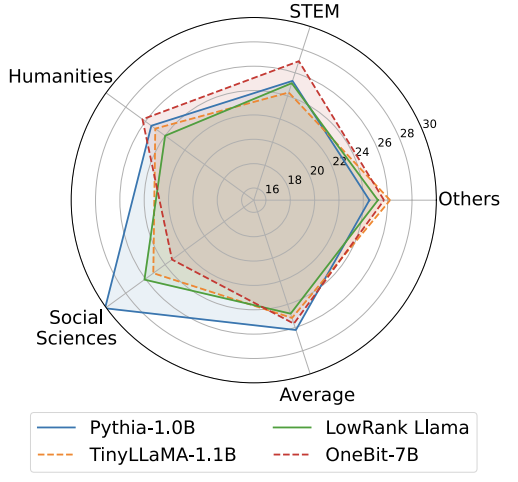
Figure 5: Comparison of world knowledge
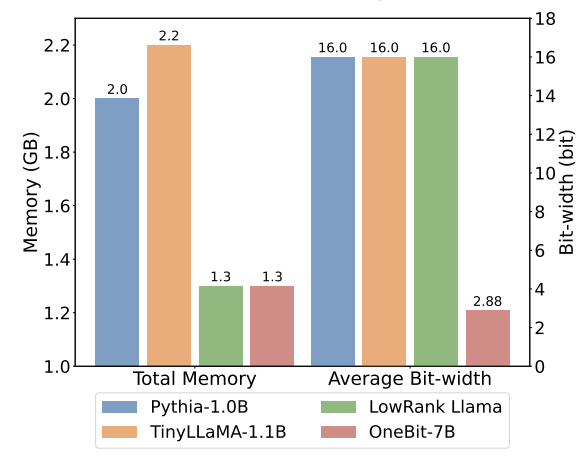
Figure 6: Space occupation and average bit width of several models
Figure 4 - Figure 6 also compare the space occupation and performance loss of several types of small models, which are obtained through different channels: including two fully trained models Pythia-1.0B and TinyLLaMA-1.1B, and through low-rank LowRank Llama and OneBit-7B obtained by decomposition. It can be seen that although OneBit-7B has the smallest average bit width and occupies the smallest space, it is still better than other models in common sense reasoning capabilities. The author also pointed out that models face serious knowledge forgetting in the field of social sciences. Overall, the OneBit-7B demonstrates its practical value. As shown in Figure 7, the OneBit quantized LLaMA-7B model demonstrates smooth text generation capabilities after fine-tuning instructions.

Figure 7: The capabilities of the LLaMA-7B model quantified by the OneBit framework
Discussion and analysis
1. Efficiency
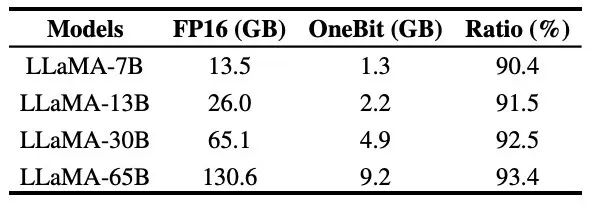
##Table 3: OneBit in different LLaMA models The compression ratio of
Table 3 shows the compression ratio of OneBit for LLaMA models of different sizes. It can be seen that the compression ratio of OneBit's models exceeds 90%. This compression capability is unprecedented. It is worth noting that as the model increases, the compression ratio of OneBit becomes higher. This is because the proportion of parameters in the Embedding layer that do not participate in quantization becomes smaller and smaller. As mentioned earlier, the larger the model, the greater the performance gain brought by OneBit, which shows the advantage of OneBit on larger models.
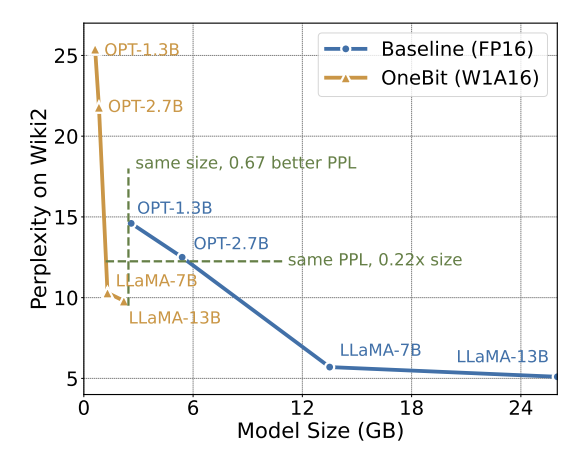
Figure 8: Model size and performance trade-off
Although ultra-low bit quantization may cause There is a certain performance penalty, but as shown in Figure 8, it strikes a good balance between size and performance. The authors believe that compressing model size is important, especially when deploying models on mobile devices.
In addition, the author also pointed out the computational advantages of the 1-bit quantization model. Since the parameters are purely binary, they can be represented in 1 bit by 0/1, which undoubtedly saves a lot of space. The element multiplication of matrix multiplication in high-precision models can be turned into efficient bit operations. Matrix product can be completed with only bit assignment and addition, which has great application prospects.
2. Robustness
Binary networks generally face the problems of unstable training and difficult convergence. Thanks to the high-precision value vector introduced by the author, both forward calculation and backward calculation of model training are very stable. BitNet proposed a 1-bit model structure earlier, but this structure has difficulty in transferring capabilities from a fully trained high-precision model. As shown in Figure 9, the author tried a variety of different learning rates to test the transfer learning ability of BitNet, and found that its convergence was difficult under the guidance of a teacher, which also proved the stable training value of OneBit.
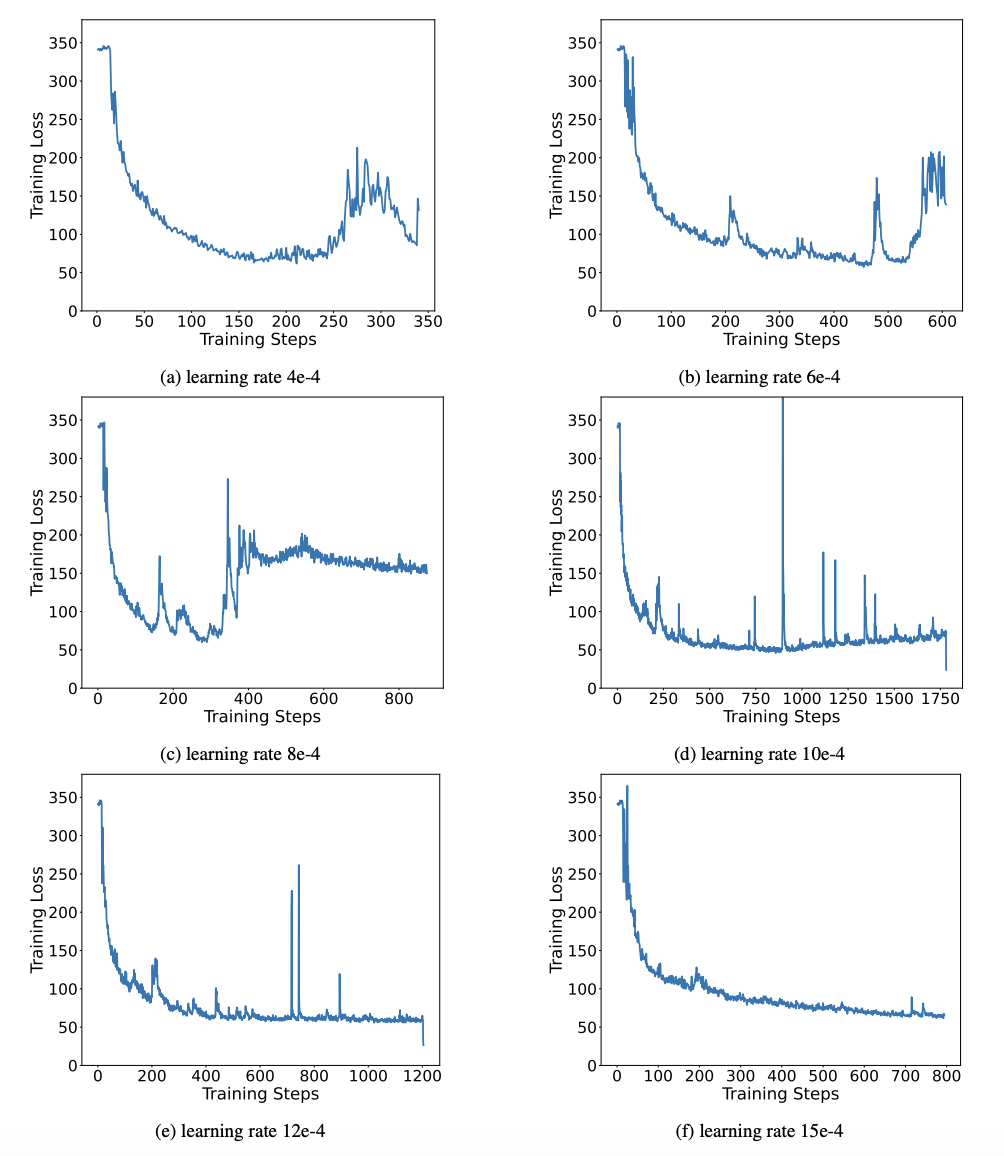
Figure 9: Quantification ability of BitNet after training under various learning rates
Paper Finally, the author also suggests possible future research directions for ultra-low bit width. For example, find a better parameter initialization method, less training cost, or further consider the quantization of activation values.
For more technical details, please see the original paper.
The above is the detailed content of Tsinghua University and Harbin Institute of Technology have compressed large models to 1 bit, and the desire to run large models on mobile phones is about to come true!. For more information, please follow other related articles on the PHP Chinese website!

Hot Article

Hot tools Tags

Hot Article

Hot Article Tags

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
May 07, 2024 pm 04:13 PM
The world's most powerful open source MoE model is here, with Chinese capabilities comparable to GPT-4, and the price is only nearly one percent of GPT-4-Turbo
 KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
Jun 01, 2024 pm 10:03 PM
KAN, which replaces MLP, has been extended to convolution by open source projects
 Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
Apr 01, 2024 pm 07:46 PM
Google is ecstatic: JAX performance surpasses Pytorch and TensorFlow! It may become the fastest choice for GPU inference training
 Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
Apr 18, 2024 pm 07:58 PM
Hello, electric Atlas! Boston Dynamics robot comes back to life, 180-degree weird moves scare Musk
 AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
Apr 09, 2024 am 11:52 AM
AI subverts mathematical research! Fields Medal winner and Chinese-American mathematician led 11 top-ranked papers | Liked by Terence Tao
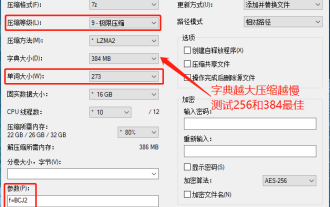 7-zip maximum compression rate setting, how to compress 7zip to the minimum
Jun 18, 2024 pm 06:12 PM
7-zip maximum compression rate setting, how to compress 7zip to the minimum
Jun 18, 2024 pm 06:12 PM
7-zip maximum compression rate setting, how to compress 7zip to the minimum
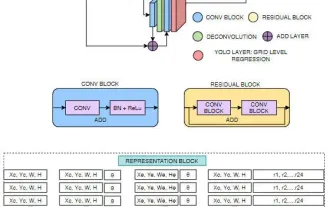 FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
Apr 26, 2024 am 11:37 AM
FisheyeDetNet: the first target detection algorithm based on fisheye camera
 Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!
May 06, 2024 pm 04:13 PM
Tesla robots work in factories, Musk: The degree of freedom of hands will reach 22 this year!






