 Technology peripherals
Technology peripherals
 AI
AI
 The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.
The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.
The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.

Editor | XS
Nature published two important research results in November 2023: protein synthesis technology Chroma and crystal material design method GNoME. Both studies adopted graph neural networks as a tool for processing scientific data.
In fact, graph neural networks, especially geometric graph neural networks, have always been an important tool for scientific intelligence (AI for Science) research. This is because physical systems such as particles, molecules, proteins, and crystals in the scientific field can be modeled into a special data structure—geometric graphs.
Different from general topological diagrams, in order to better describe the physical system, geometric diagrams add indispensable spatial information and need to meet the physical symmetry of translation, rotation and flipping. In view of the superiority of geometric graph neural networks for modeling physical systems, various methods have emerged in recent years, and the number of papers continues to grow.
Recently, Renmin University of China and Hillhouse, together with Tencent AI Lab, Tsinghua University, Stanford and other institutions, released a review paper: "A Survey of Geometric Graph Neural Networks: Data Structures, Models and Applications". Based on a brief introduction to theoretical knowledge such as group theory and symmetry, this review systematically reviews the relevant geometric graph neural network literature from data structures and models to numerous scientific applications.

Paper link: https://arxiv.org/abs/2403.00485
GitHub link: https:/ /github.com/RUC-GLAD/GGNN4Science
In this review, the author investigated more than 300 references, summarized 3 different geometric graph neural network models, and introduced particle-oriented A total of 23 related methods for different tasks on various scientific data such as molecules, proteins, etc., and more than 50 related evaluation data sets have been collected. Finally, the review looks forward to future research directions, including geometric graph basic models, combination with large language models, etc.
The following is a brief introduction to each chapter.

Geometric graph data structure
Geometric graph consists of adjacency matrix, node characteristics, node geometric information (such as coordinates). In Euclidean space, geometric figures usually show physical symmetries of translation, rotation and reflection. Groups are generally used to describe these transformations, including Euclidean group, translation group, orthogonal group, permutation group, etc. Intuitively, it can be understood as a combination of four operations: displacement, translation, rotation, and flipping in a certain order.
For many AI for Science fields, geometric graphs are a powerful and versatile representation method that can be used to represent many physical systems, including small molecules, proteins, crystals, physical point clouds, etc.
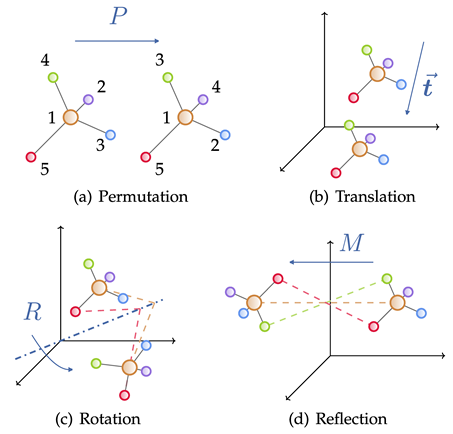
Geometric graph neural network model
According to the requirements for symmetry of the solution goals in actual problems, this article uses geometric graph neural network Networks are divided into three categories: invariant (invariant) model, equivariant (equivariant) model, and Geometric Graph Transformer inspired by the Transformer architecture. The equivariant model is subdivided into scalarization-based model (Scalarization-Based Model) and based on High-Degree Steerable Model of spherical harmonization. According to the above rules, the article collects and categorizes well-known geometric graph neural network models in recent years.
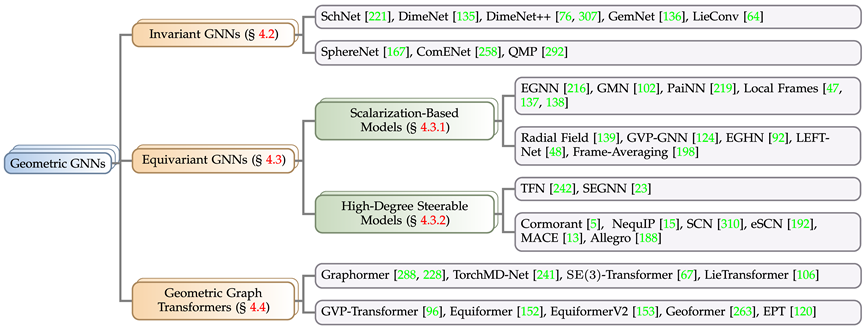
Here we briefly introduce the invariant model (SchNet[1]), the scalarization method model (EGNN[2]), and the high-order scalable model through the representative work of each branch. The correlation and difference between manipulation models (TFN[3]). It can be found that all three use message passing mechanisms, but the latter two, which are equivariant models, introduce an additional geometric message passing.
The invariant model mainly uses the characteristics of the node itself (such as atom type, mass, charge, etc.) and the invariant characteristics between atoms (such as distance, angle [4], dihedral angle [5]), etc. Message computation is performed and subsequently propagated.
On top of this, the scalarization method additionally introduces geometric information through the coordinate difference between nodes, and uses the invariant information as the weight of the geometric information for linear combination, realizing the introduction of equivariance.
High-order controllable models use high-order Spherical Harmonics and Wigner-D matrices to represent the geometric information of the system. This method uses the Clebsch–Gordan coefficient in quantum mechanics to control the order of irreducible representation. numbers, thereby realizing the geometric message passing process.
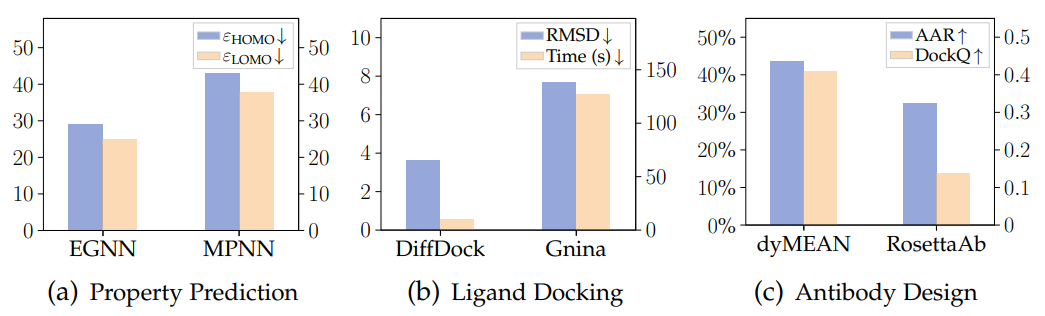
Geometric graph neural network has greatly improved the accuracy through the symmetry guaranteed by this type of design, and it also shines in the generation task.
The following figure is the results of the three tasks of molecular property prediction, protein-ligand docking and antibody design (generation) using the geometric graph neural network and the traditional model on the three data sets of QM9, PDBBind and SabDab. The advantages of geometric graph neural networks can be clearly seen.
Scientific Applications
In terms of scientific applications, the review covers physics (particles), biochemistry (small molecules, proteins) As well as other application scenarios such as crystals, starting from the task definition and the type of symmetry required to ensure, the commonly used data sets in each task and the classic model design ideas in this type of tasks are introduced.

The above table shows common tasks and classic models in various fields. Among them, according to single instance and multiple instances (such as chemical reactions, which require the participation of multiple molecules), the article is separate Three areas are distinguished: small molecule-small molecule, small molecule-protein, and protein-protein.
In order to better facilitate model design and experiment development in the field, the article counts common data sets and benchmarks (benchmarks) for two types of tasks based on single instance and multiple instances, and records samples of different data sets. Quantity and type of tasks.
The following table summarizes common single-instance task data sets.

The following table summarizes common multi-instance task data sets.

Future Outlook
The article makes a preliminary outlook on several aspects, hoping to serve as a starting point:
1. Geometric graph basic model
The advantages of using a unified basic model in various tasks and fields have been fully reflected in the significant progress of the GPT series models. How to carry out reasonable design in task space, data space and model space, so as to introduce this idea into the design of geometric graph neural network, is still an interesting open problem.
2. Efficient cycle of model training and real-world experimental validation
Acquisition of scientific data is expensive and time-consuming, and only evaluation on independent data sets Models cannot directly reflect feedback from the real world. The importance of how to achieve efficient model-reality iterative experimental paradigms similar to GNoME (which integrates an end-to-end pipeline including graph network training, density functional theory calculations and automated laboratories for materials discovery and synthesis) will It will increase day by day.
3. Integration with Large Language Models (LLMs)
Large Language Models (LLMs) have been widely proven to have rich knowledge, covering various fields. Although there have been some works utilizing LLMs for certain tasks such as molecular property prediction and drug design, they only operate on primitives or molecular graphs. How to organically combine them with geometric graph neural networks so that they can process 3D structural information and perform prediction or generation on 3D structures is still quite challenging.
4. Relaxation of equivariance constraints
There is no doubt that equivariance is crucial to enhance data efficiency and model generalization ability, but it is worth noting that , too strong equivariance constraints can sometimes be too restrictive of the model, potentially harming its performance. Therefore, how to balance the equivariance and adaptability of the designed model is a very interesting question. Exploration in this area can not only enrich our understanding of model behavior, but also pave the way for the development of more robust and general solutions with wider applicability.
References
[1] Schütt K, Kindermans P J, Sauceda Felix H E, et al. Schnet: A continuous-filter convolutional neural network for modeling quantum interactions[ J]. Advances in neural information processing systems, 2017, 30.
[2] Satorras V G, Hoogeboom E, Welling M. E (n) equivariant graph neural networks[C]//International conference on machine learning. PMLR, 2021: 9323-9332.
[3] Thomas N, Smidt T, Kearnes S, et al. Tensor field networks: Rotation-and translation-equivariant neural networks for 3d point clouds[J]. arXiv preprint arXiv:1802.08219, 2018.
[4] Gasteiger J, Groß J, Günnemann S. Directional Message Passing for Molecular Graphs[C]//International Conference on Learning Representations. 2019.
[5] Gasteiger J, Becker F, Günnemann S. Gemnet: Universal directional graph neural networks for molecules[J]. Advances in Neural Information Processing Systems, 2021, 34: 6790-6802.
[6] Merchant A, Batzner S, Schoenholz S S, et al. Scaling deep learning for materials discovery[J]. Nature, 2023, 624(7990): 80-85.
The above is the detailed content of The cornerstone of AI4Science: geometric graph neural network, the most comprehensive review is here! Renmin University of China Hillhouse jointly released Tencent AI lab, Tsinghua University, Stanford, etc.. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1393
1393
 52
52
 38
38
 112
112
 Breaking through the boundaries of traditional defect detection, 'Defect Spectrum' achieves ultra-high-precision and rich semantic industrial defect detection for the first time.
Jul 26, 2024 pm 05:38 PM
Breaking through the boundaries of traditional defect detection, 'Defect Spectrum' achieves ultra-high-precision and rich semantic industrial defect detection for the first time.
Jul 26, 2024 pm 05:38 PM
In modern manufacturing, accurate defect detection is not only the key to ensuring product quality, but also the core of improving production efficiency. However, existing defect detection datasets often lack the accuracy and semantic richness required for practical applications, resulting in models unable to identify specific defect categories or locations. In order to solve this problem, a top research team composed of Hong Kong University of Science and Technology Guangzhou and Simou Technology innovatively developed the "DefectSpectrum" data set, which provides detailed and semantically rich large-scale annotation of industrial defects. As shown in Table 1, compared with other industrial data sets, the "DefectSpectrum" data set provides the most defect annotations (5438 defect samples) and the most detailed defect classification (125 defect categories
 NVIDIA dialogue model ChatQA has evolved to version 2.0, with the context length mentioned at 128K
Jul 26, 2024 am 08:40 AM
NVIDIA dialogue model ChatQA has evolved to version 2.0, with the context length mentioned at 128K
Jul 26, 2024 am 08:40 AM
The open LLM community is an era when a hundred flowers bloom and compete. You can see Llama-3-70B-Instruct, QWen2-72B-Instruct, Nemotron-4-340B-Instruct, Mixtral-8x22BInstruct-v0.1 and many other excellent performers. Model. However, compared with proprietary large models represented by GPT-4-Turbo, open models still have significant gaps in many fields. In addition to general models, some open models that specialize in key areas have been developed, such as DeepSeek-Coder-V2 for programming and mathematics, and InternVL for visual-language tasks.
 Training with millions of crystal data to solve the crystallographic phase problem, the deep learning method PhAI is published in Science
Aug 08, 2024 pm 09:22 PM
Training with millions of crystal data to solve the crystallographic phase problem, the deep learning method PhAI is published in Science
Aug 08, 2024 pm 09:22 PM
Editor |KX To this day, the structural detail and precision determined by crystallography, from simple metals to large membrane proteins, are unmatched by any other method. However, the biggest challenge, the so-called phase problem, remains retrieving phase information from experimentally determined amplitudes. Researchers at the University of Copenhagen in Denmark have developed a deep learning method called PhAI to solve crystal phase problems. A deep learning neural network trained using millions of artificial crystal structures and their corresponding synthetic diffraction data can generate accurate electron density maps. The study shows that this deep learning-based ab initio structural solution method can solve the phase problem at a resolution of only 2 Angstroms, which is equivalent to only 10% to 20% of the data available at atomic resolution, while traditional ab initio Calculation
 Google AI won the IMO Mathematical Olympiad silver medal, the mathematical reasoning model AlphaProof was launched, and reinforcement learning is so back
Jul 26, 2024 pm 02:40 PM
Google AI won the IMO Mathematical Olympiad silver medal, the mathematical reasoning model AlphaProof was launched, and reinforcement learning is so back
Jul 26, 2024 pm 02:40 PM
For AI, Mathematical Olympiad is no longer a problem. On Thursday, Google DeepMind's artificial intelligence completed a feat: using AI to solve the real question of this year's International Mathematical Olympiad IMO, and it was just one step away from winning the gold medal. The IMO competition that just ended last week had six questions involving algebra, combinatorics, geometry and number theory. The hybrid AI system proposed by Google got four questions right and scored 28 points, reaching the silver medal level. Earlier this month, UCLA tenured professor Terence Tao had just promoted the AI Mathematical Olympiad (AIMO Progress Award) with a million-dollar prize. Unexpectedly, the level of AI problem solving had improved to this level before July. Do the questions simultaneously on IMO. The most difficult thing to do correctly is IMO, which has the longest history, the largest scale, and the most negative
 Nature's point of view: The testing of artificial intelligence in medicine is in chaos. What should be done?
Aug 22, 2024 pm 04:37 PM
Nature's point of view: The testing of artificial intelligence in medicine is in chaos. What should be done?
Aug 22, 2024 pm 04:37 PM
Editor | ScienceAI Based on limited clinical data, hundreds of medical algorithms have been approved. Scientists are debating who should test the tools and how best to do so. Devin Singh witnessed a pediatric patient in the emergency room suffer cardiac arrest while waiting for treatment for a long time, which prompted him to explore the application of AI to shorten wait times. Using triage data from SickKids emergency rooms, Singh and colleagues built a series of AI models that provide potential diagnoses and recommend tests. One study showed that these models can speed up doctor visits by 22.3%, speeding up the processing of results by nearly 3 hours per patient requiring a medical test. However, the success of artificial intelligence algorithms in research only verifies this
 Three secrets for deploying large models in the cloud
Apr 24, 2024 pm 03:00 PM
Three secrets for deploying large models in the cloud
Apr 24, 2024 pm 03:00 PM
Compilation|Produced by Xingxuan|51CTO Technology Stack (WeChat ID: blog51cto) In the past two years, I have been more involved in generative AI projects using large language models (LLMs) rather than traditional systems. I'm starting to miss serverless cloud computing. Their applications range from enhancing conversational AI to providing complex analytics solutions for various industries, and many other capabilities. Many enterprises deploy these models on cloud platforms because public cloud providers already provide a ready-made ecosystem and it is the path of least resistance. However, it doesn't come cheap. The cloud also offers other benefits such as scalability, efficiency and advanced computing capabilities (GPUs available on demand). There are some little-known aspects of deploying LLM on public cloud platforms
 PRO | Why are large models based on MoE more worthy of attention?
Aug 07, 2024 pm 07:08 PM
PRO | Why are large models based on MoE more worthy of attention?
Aug 07, 2024 pm 07:08 PM
In 2023, almost every field of AI is evolving at an unprecedented speed. At the same time, AI is constantly pushing the technological boundaries of key tracks such as embodied intelligence and autonomous driving. Under the multi-modal trend, will the situation of Transformer as the mainstream architecture of AI large models be shaken? Why has exploring large models based on MoE (Mixed of Experts) architecture become a new trend in the industry? Can Large Vision Models (LVM) become a new breakthrough in general vision? ...From the 2023 PRO member newsletter of this site released in the past six months, we have selected 10 special interpretations that provide in-depth analysis of technological trends and industrial changes in the above fields to help you achieve your goals in the new year. be prepared. This interpretation comes from Week50 2023
 To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
To provide a new scientific and complex question answering benchmark and evaluation system for large models, UNSW, Argonne, University of Chicago and other institutions jointly launched the SciQAG framework
Jul 25, 2024 am 06:42 AM
Editor |ScienceAI Question Answering (QA) data set plays a vital role in promoting natural language processing (NLP) research. High-quality QA data sets can not only be used to fine-tune models, but also effectively evaluate the capabilities of large language models (LLM), especially the ability to understand and reason about scientific knowledge. Although there are currently many scientific QA data sets covering medicine, chemistry, biology and other fields, these data sets still have some shortcomings. First, the data form is relatively simple, most of which are multiple-choice questions. They are easy to evaluate, but limit the model's answer selection range and cannot fully test the model's ability to answer scientific questions. In contrast, open-ended Q&A



