Tsinghua Yao class undergraduates published two works in a row, the biggest improvement in ten years: matrix multiplication is close to the theoretical optimal

By eliminating "hidden inefficiencies", computer scientists have come up with a new way to multiply large matrices faster than ever before.

Matrix multiplication, as the basic operation of many GPU operators, plays an important role in high-performance computing and is also a key component of applications such as AI. Although the algorithm itself is relatively simple, efforts have been made to optimize it over the years in order to achieve higher speeds. However, the extent of optimization has been somewhat limited.

In the latest issue of Quantum Magazine, we found two papers that can speed up matrix multiplication. In the writing of these two papers, a senior undergraduate student from Yao Class at Tsinghua University actively participated, which brought new prospects for algorithm improvement in this field.

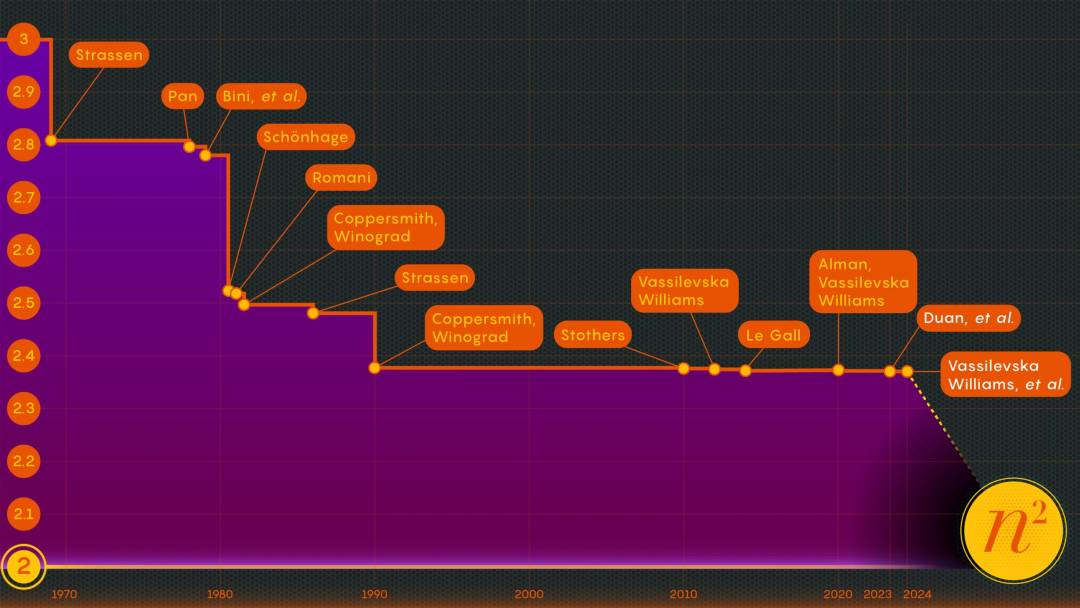
New "singularity" appears in the improvement of matrix multiplication

Computer scientists are a group of very demanding people. What they pursue is not only solving problems, but also achieving goals in the most efficient way.

Take the example of multiplying matrices or arrays of numbers. In 1812, French mathematician Jacques Philippe Marie Binet proposed a set of basic rules that are still taught to students today. This set of rules is widely used, but in recent years some mathematicians have discovered ways to simplify and speed up the process.

####################################################################################################################### French mathematician Jacques Philippe Marie Binet. ############Currently, accelerating the matrix multiplication process has become an intersection of mathematics and computer science. Researchers have been working to improve this process, although progress has been limited in recent decades. François Le Gall, a computer scientist at Nagoya University, points out that numerical improvements to matrix multiplication have been slow and difficult to achieve since 1987. He believes that under the current circumstances, further improving the efficiency of matrix multiplication faces huge challenges and requires more innovation and breakthroughs. Despite the difficulties, scientists are still working tirelessly to seek breakthroughs, hoping to find new methods and techniques to improve the calculation speed and efficiency of matrix multiplication. This shows that matrix multiplication optimization is still a challenging topic and requires the collective efforts of Ran Duan and Renfei Zhou of Tsinghua University and Hongxun Wu of the University of California, Berkeley, to solve this long-term problem recently. Important progress has been made on existing problems, and their research results are presented in detail in an 87-page paper. Le Gall spoke highly of the work of these three researchers. He believed that although the improvement was relatively small, it was an unprecedented conceptual breakthrough. ######This paper was accepted by FOCS 2023, the top conference in the field of computer science. ###############Paper v1 will be released in October 2022, v5 in November 2023. Paper address: https://arxiv.org/abs/2210.10173###### Among them, Duan Ran is an associate professor at the Institute of Interdisciplinary Information at Tsinghua University. His main research directions are graph theory algorithms, data structures, and computing theory. Hongxun Wu is a second-year doctoral student at the University of California, Berkeley, and a graduate of the Yao Class of Tsinghua University. ######Zhou Renfei is a senior undergraduate student in the Yao Class of 2020 at Tsinghua University, majoring in theoretical computer science (TCS). He works primarily on (concise) data structures and fast matrix multiplication, and has broad interests in other areas of TCS such as streaming algorithms, game theory, and online algorithms. ######Previously, Zhou Renfei had published many papers at FOCS/SODA, a top conference in theoretical computer science. ################The paper by three researchers reveals previously unknown and untapped potential sources of improvements that are already bearing fruit. A second paper published in January 2024 (also co-authored by Renfei Zhou) builds on this and shows how matrix multiplication can be further enhanced. ###############Paper address: https://epubs.siam.org/doi/10.1137/1.9781611977912.134###### Harvard University theoretical computer scientist William Kuszmaul responded to this Said that this is a major technological breakthrough and the biggest improvement in matrix multiplication we have seen in more than ten years. #########What issues should be improved in matrix multiplication######

Matrix multiplication may seem like an obscure problem, but it is a basic computational operation. It's incorporated into most of the algorithms people use every day for a variety of tasks, from displaying clearer computer graphics to solving logistics problems in network theory. Just like in other areas of computing, speed is of the essence. Even small improvements could ultimately significantly reduce the time, computing power, and money required. But for now, theorists are mainly interested in figuring out just how fast the process can go.

The traditional method of multiplying two n×n matrices - that is, multiplying the numbers in each row of the first matrix by the numbers in each column of the second matrix - requires n³ independent operations Multiplication operation. For a 2 by 2 matrix, this means 2³, or 8 multiplications.

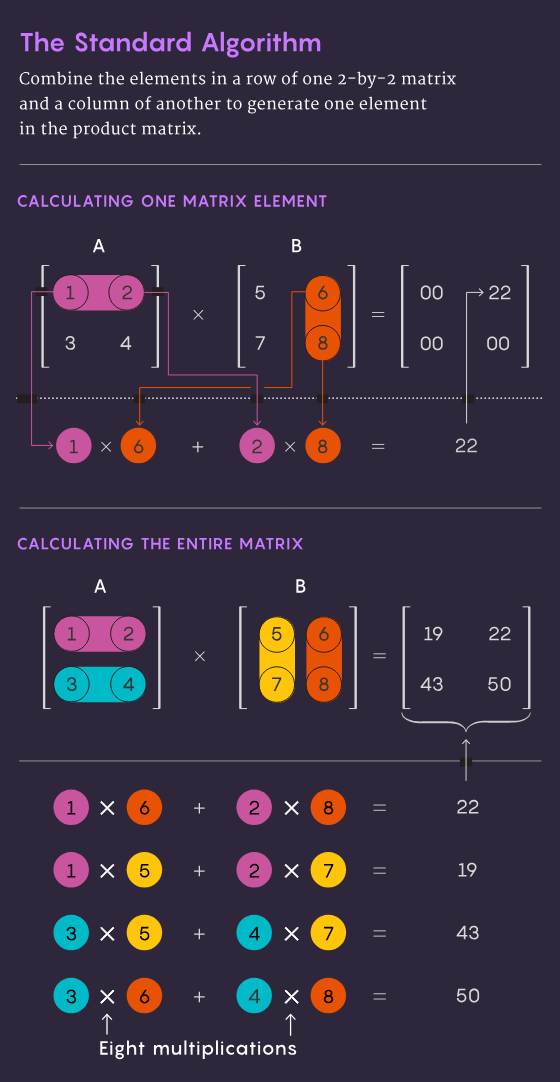
In 1969, mathematician Volker Strassen discovered a more elegant method that can complete a 2×2 matrix with only 7 multiplication steps and 18 addition steps. multiplication operation. Two years later, computer scientist Shmuel Winograd showed that 7-step multiplication was indeed the absolute minimum for a 2×2 matrix.

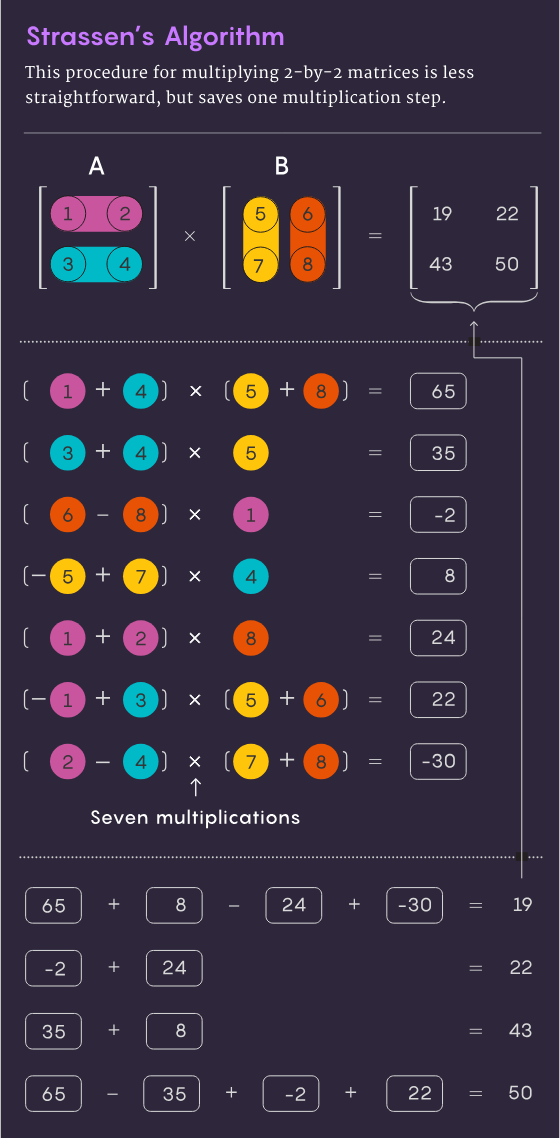
Strassen used the same idea to show that all larger n×n matrices can also be multiplied in fewer than n3 steps. A key element in this strategy involves a procedure called decomposition: decomposing a large matrix into smaller submatrices, which may end up being as small as 2×2 or even 1×1 (just a single number).

The reason for breaking giant arrays into small pieces is quite simple. Virginia Vassilevska Williams, a computer scientist at MIT, said: "For a large matrix (such as a 100×100 matrix), it is difficult for humans to think of the most The best algorithm." Even the 3-by-3 matrix is ​​not completely solved yet. "However, one can use fast algorithms that have been developed for small matrices to obtain fast algorithms for larger matrices."

The researchers determined that the key to speed lies in reducing the number of multiplication steps, moving the exponent from n3 as much as possible (traditional method) lowered. The lowest possible value n² is basically the time it takes to write the answer. Computer scientists call this exponent Ω, or ω. nω is the minimum number of steps required to successfully multiply two n×n matrices as n gets larger. Zhou Renfei, who is also a co-author of the January 2024 paper, said: "The focus of this work is to see how close you can get to 2 and whether it can be achieved theoretically."

Laser Method

In 1986, Strassen achieved another major breakthrough when he introduced the laser method of matrix multiplication. Strassen used this to determine an upper limit for ω of 2.48. Although the method is just one step in large matrix multiplication, it is one of the most important because researchers are constantly improving it.

A year later, Winograd and Don Coppersmith introduced a new algorithm that perfectly complemented the laser method. This combination of tools was used in almost all subsequent research on accelerating matrix multiplication.

Here’s a simplified way to see how these different elements fit together. Let's start with two large matrices A and B and multiply them. First, you break them into many smaller submatrices, sometimes called chunks. Next, you can use Coppersmith and Winograd's algorithms as a guide for processing and ultimately assembling these blocks. "It tells me what to multiply, what to add, and which elements are where in the product matrix C," Vassilevska Williams said. "It's just a 'recipe' for building C from A and B."

However, there is a problem: sometimes you get blocks with common elements. Retaining these common elements would be equivalent to counting these elements twice, so at some point, these overlaps need to be eliminated. The researchers solved this problem by "killing" the blocks they were in - setting their components to zero to remove them from the calculation.

##                                                                                                                                                                                                 Virginia Vassilevska Williams was part of a team that improved a new method for matrix multiplication and she came up with the fastest method currently available.

This is where Strassen’s laser method finally comes into play. "The laser method is usually very effective and often finds a good way to eliminate overlapping sub-blocks," Le Gall said. After the laser has eliminated all overlap, you can construct the final product matrix C.

Combining these various techniques results in an algorithm that multiplies two matrices with as few total multiplications as possible, at least in theory. The laser method is not intended for practical applications; it is just an ideal way of thinking about matrix multiplication. Zhou Renfei said, "We have never run this method on a computer, we analyze it."

It is this analysis that has led to ω's biggest improvement in more than ten years.

The "hidden loss" discovered

In the first paper "Faster Matrix Multiplication via Asymmetric Hashing" by Duan Ran, Zhou Renfei and Hongxun Wu, they showed , the process of Strassen's algorithm can be greatly accelerated. This is all thanks to a concept they call "hidden loss." Zhou Renfei said that the concept was deeply hidden in previous analysis and was the result of inadvertently eliminating too many blocks.

The laser method works by marking overlapping blocks as garbage and scheduling them for processing, while other blocks are considered valuable and will be saved. However, the selection process is somewhat random. In fact, blocks marked as garbage may end up being useful.

This isn’t entirely surprising, but by examining many random selections, Duan Ran’s team determined that the laser method systematically underestimates the value of blocks, so more blocks should be saved and fewer thrown away. And, as is often the case, less waste translates into greater efficiency.

Regarding Duan Ran’s team’s approach, Le Gall believes that “more blocks can be retained without overlapping. This approach achieves a faster matrix multiplication algorithm.”

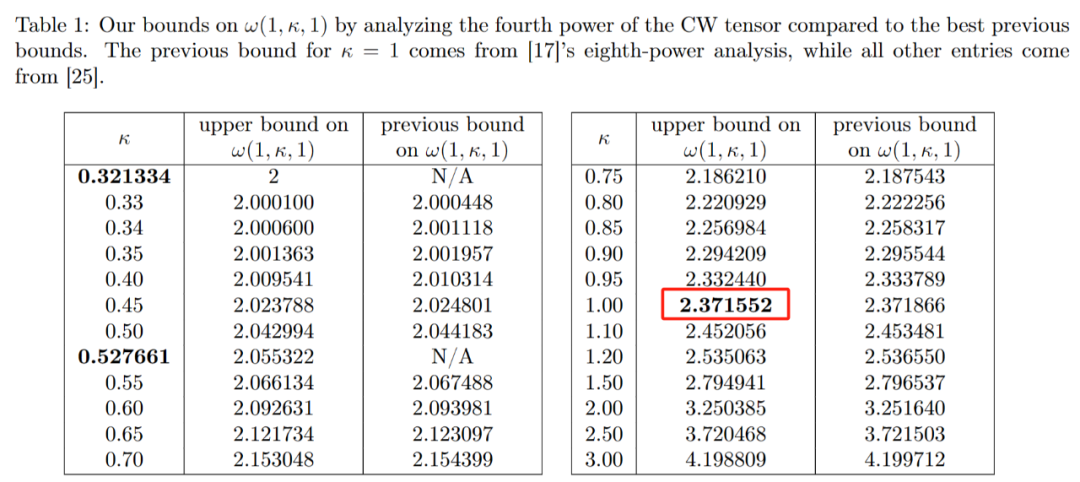
It proves this After this kind of loss existed, Duan Ran's team modified the way of laser marking blocks, thus greatly reducing waste. They set a new cap on ω around 2.371866, which is an improvement over the 2.3728596 cap set by Josh Alman and Vassilevska Williams in 2020.

This may seem like a small change, lowering the upper limit by about 0.001, but it's the biggest improvement scientists have seen since 2010. In comparison, Vassilevska Williams and Alman's 2020 results improved by just 0.00001 from their previous results.

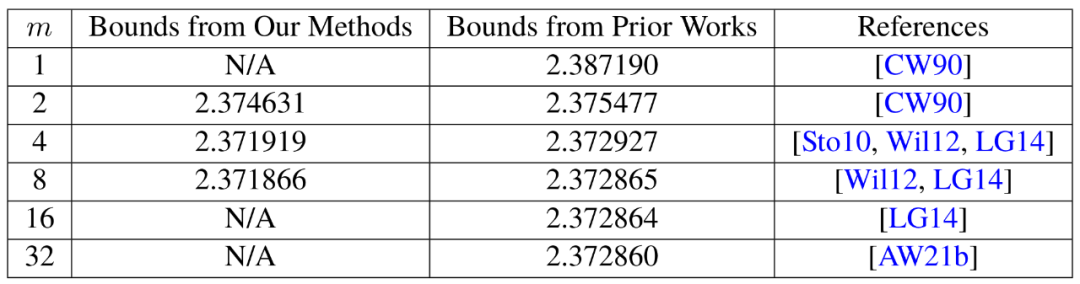
Of course, the most exciting thing for researchers was not just the new record itself, which didn't last long. In fact, this paper reveals a new avenue for improvement that had previously gone completely unnoticed.

Le Gall says everyone has relied on the same laser method for nearly four decades. With the emergence of papers by three researchers including Duan Ran, we can do better.

Therefore, the January 2024 paper co-authored by Zhou Renfei improved this new method and further reduced the hidden loss. They further raised the upper limit of ω, lowering it to 2.371552.

Researchers also used the same method to improve the multiplication process of rectangular (n×m) matrices, which has widespread use in graph theory, machine learning, and other fields. application.

Some further progress along these directions is almost certain, but there are limits. In 2015, Le Gall and two co-authors showed that the current method, namely the laser method, coupled with the method of Coppersmith and Winograd, was unable to obtain ω below 2.3078.

Le Gall said: "To improve further, you have to improve on the original method of Coppersmith and Winograd, which has not really changed since 1987." But so far, No one has come up with a better way yet. Maybe not at all.

Zhou Renfei said: "Improving ω is actually part of understanding this problem. If we can understand this problem well, we can design better algorithms. However, people's understanding of this ancient problem is still unclear. At a very early stage."

^{Original link:}

^{https://www.quantamagazine.org/new-breakthrough-brings- matrix-multiplication-closer-to-ideal-20240307/}

The above is the detailed content of Tsinghua Yao class undergraduates published two works in a row, the biggest improvement in ten years: matrix multiplication is close to the theoretical optimal. For more information, please follow other related articles on the PHP Chinese website!