Make large models 'slim down' by 90%! Tsinghua University & Harbin Institute of Technology proposed an extreme compression solution: 1-bit quantization, while retaining 83% of the capacity

Quantification, pruning and other compression operations on large models are the most common part of deployment.

However, how big is this limit?

A joint study by Tsinghua University and Harbin Institute of Technology gave the answer:

90%.

They proposed a large model 1-bit extreme compression framework OneBit, which for the first time achieved weight compression of large models exceeding 90% and retained most (83%) capabilities .

It can be said that playing is about "wanting and wanting"~

Let's take a look.

The 1-bit quantization method for large models is here

From pruning and quantization to knowledge distillation and low-rank weight decomposition, large models can already compress a quarter of the weight with almost no loss.

Weight quantization typically converts the parameters of a large model into a low bit-width representation. This can be achieved by transforming a fully trained model (PTQ) or introducing a quantization step during training (QAT). This approach helps reduce the computational and storage requirements of the model, thereby improving model efficiency and performance. By quantizing weights, the size of the model can be significantly reduced, making it more suitable for deployment in resource-constrained environments, while also

However, existing quantization methods face severe performance losses below 3bit, This is mainly due to:

1. The existing parameter low bit width representation method has serious accuracy loss at 1 bit. When the parameters based on the Round-To-Nearest method are expressed in 1 bit, the converted scaling coefficient s and zero point z will lose their practical meaning.
2. The existing 1-bit model structure does not fully consider the importance of floating point precision. The lack of floating point parameters may affect the stability of the model calculation process and seriously reduce its own learning ability.

In order to overcome the obstacles of 1-bit ultra-low bit width quantization, the author proposes a new 1-bit model framework: OneBit, which includes a new 1-bit linear layer structure, SVID-based parameter initialization method and quantization-based perception Deep transfer learning for knowledge distillation.

This new 1-bit model quantization method can retain most of the capabilities of the original model with a huge compression range, ultra-low space occupation and limited computing cost. This is of great significance for the deployment of large models on PCs and even smartphones.

Overall Framework

The OneBit framework generally includes: a newly designed 1-bit model structure, a method of initializing quantified model parameters based on the original model, and deep capability migration based on knowledge distillation.

This newly designed 1-bit model structure can effectively overcome the serious accuracy loss problem in 1-bit quantization in previous quantization work, and shows excellent stability during training and migration.

The initialization method of the quantitative model can set a better starting point for knowledge distillation, accelerate convergence and achieve better capability transfer effects.

1. 1bit model structure

1bit requires that each weight value can only be represented by 1 bit, so there are only two possible states at most.

The author chooses ±1 as these two states. The advantage is that it represents two symbols in the digital system and has more complete functions. At the same time, it can be easily obtained through the Sign(·) function.

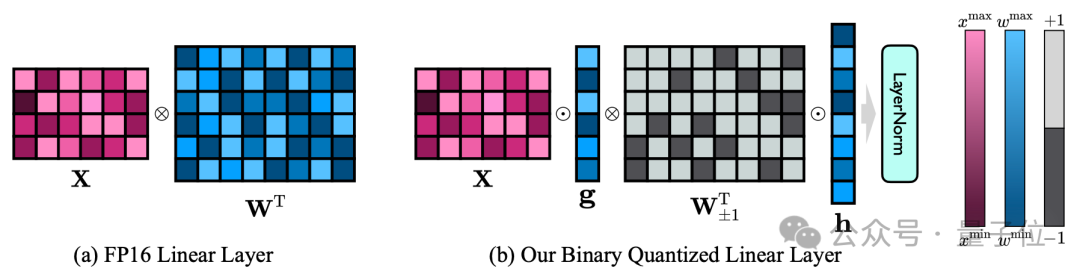
The author's 1bit model structure is achieved by replacing all linear layers of the FP16 model (except the embedding layer and lm_head) with 1bit linear layers.

In addition to the 1-bit weight obtained through the Sign(·) function, the 1-bit linear layer here also includes two other key components—the value vector of FP16 precision.

△Comparison of FP16 linear layer and OneBit linear layer

This design not only maintains the high rank of the original weight matrix, but also provides The necessary floating point precision is meaningful to ensure a stable and high-quality learning process.

As can be seen from the above figure, only the value vectors g and h maintain the FP16 format, while the weight matrix is ​​all composed of ±1.

The author can take a look at OneBit's compression capabilities through an example.

Assuming that a 40964096 FP16 linear layer is compressed, OneBit requires a 40964096 1-bit matrix and two 4096*1 FP16 value vectors.

The total number of bits is 16,908,288, and the total number of parameters is 16,785,408. On average, each parameter occupies only about 1.0073 bits.

This kind of compression range is unprecedented and can be said to be a true 1bit LLM.

2. Parameter initialization and transfer learning

In order to use the fully trained original model to better initialize the quantized model, the author proposes a new parameter matrix The decomposition method is called "value-sign independent matrix factorization (SVID)".

This matrix decomposition method separates symbols and absolute values, and performs rank-1 approximation on absolute values. Its method of approximating the original matrix parameters can be expressed as:

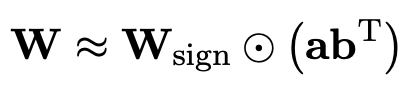
Rank-1 approximation can be achieved by common matrix factorization methods, such as singular value decomposition (SVD) and nonnegative matrix factorization (NMF).

The author mathematically shows that this SVID method can match the 1-bit model framework by exchanging the order of operations, thereby achieving parameter initialization.

In addition, the contribution of the symbolic matrix to approximating the original matrix during the decomposition process has also been proven. See the paper for details.

The author believes that an effective way to solve ultra-low bitwidth quantization of large models may be quantization-aware training QAT.

Therefore, after SVID gives the parameter starting point of the quantitative model, the author uses the original model as the teacher model and learns from it through knowledge distillation.

Specifically, the student model mainly receives guidance from the logits and hidden state of the teacher model.

During training, the values ​​of the value vector and parameter matrix will be updated, and during deployment, the quantized 1-bit parameter matrix can be used directly for calculation.

The larger the model, the better the effect

The baselines selected by the author are FP16 Transformer, GPTQ, LLM-QAT and OmniQuant.

The last three are all classic strong baselines in the field of quantification, especially OmniQuant, which is the strongest 2-bit quantization method before the author.

Since there is currently no research on 1-bit weight quantization, the author only uses 1-bit weight quantization for the OneBit framework, and adopts 2-bit quantization settings for other methods.

For distilled data, the author followed LLM-QAT and used teacher model self-sampling to generate data.

The author uses models of different sizes from 1.3B to 13B, OPT and LLaMA-1/2 in different series to prove the effectiveness of OneBit. In terms of evaluation indicators, the perplexity of the verification set and the zero-shot accuracy of common sense reasoning are used. See the paper for details.

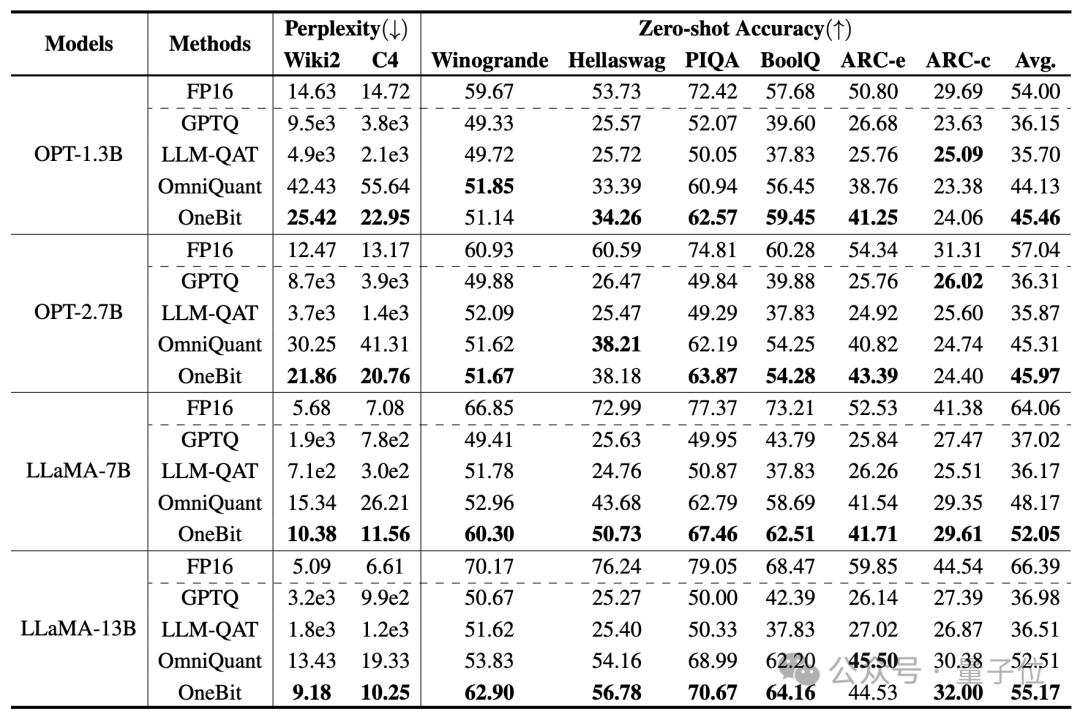
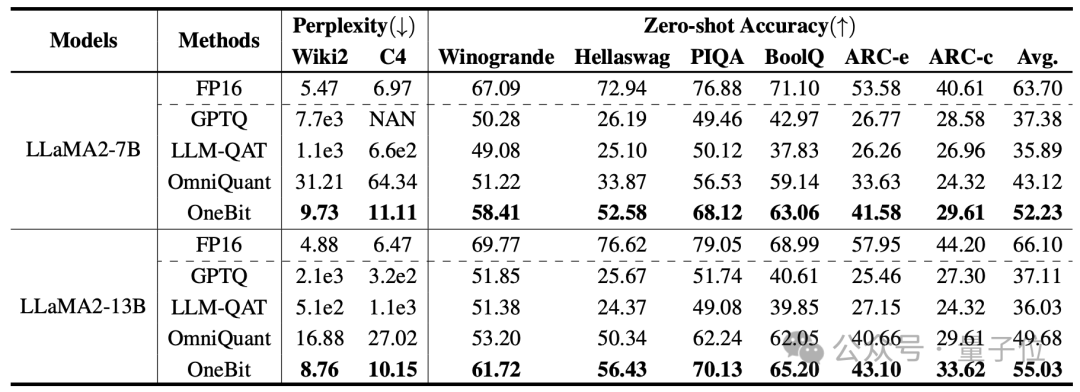
The above table shows the advantages of OneBit compared to other methods in 1-bit quantization. It is worth noting that the larger the model, the better the OneBit effect is.

As the model size increases, the OneBit quantitative model reduces the perplexity more than the FP16 model.

The following are the common sense reasoning, world knowledge and space occupation of several different small models:

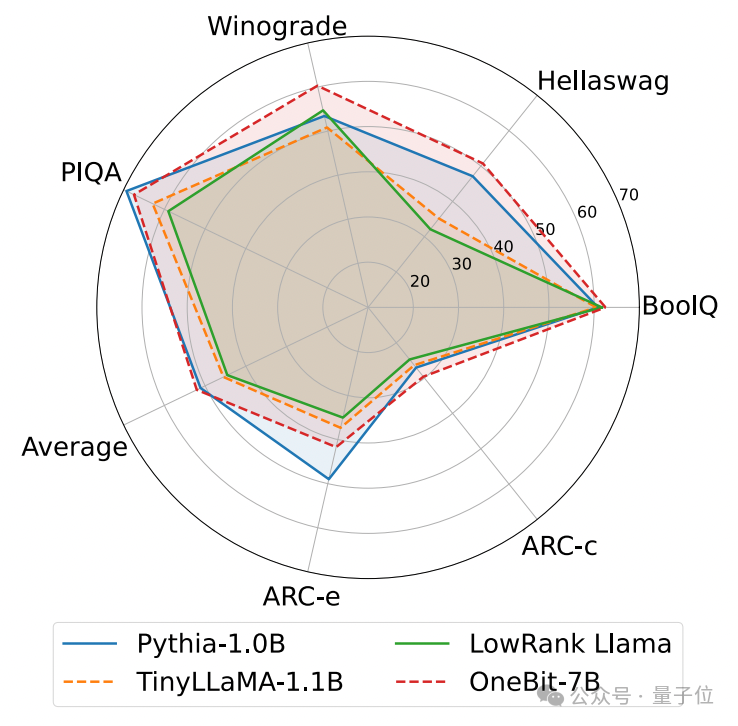
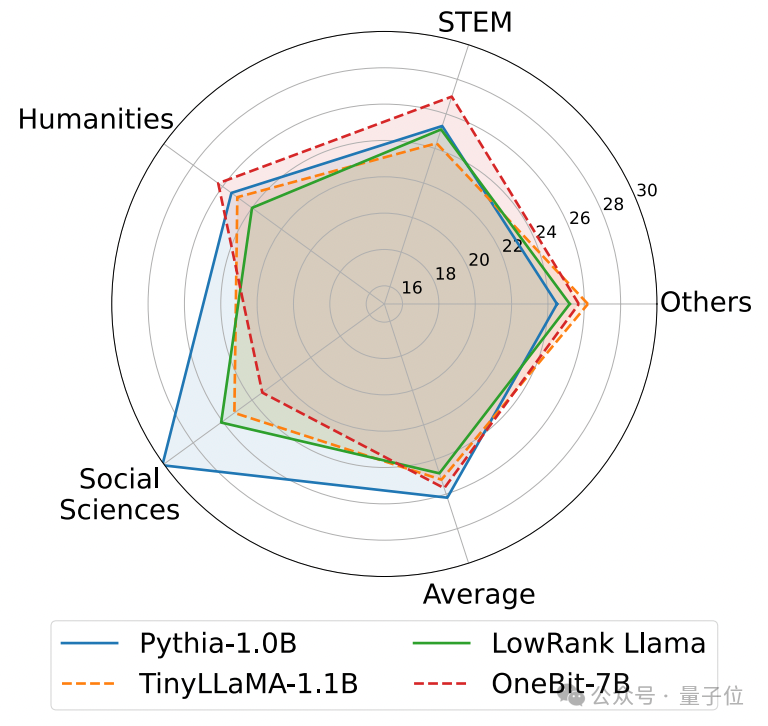
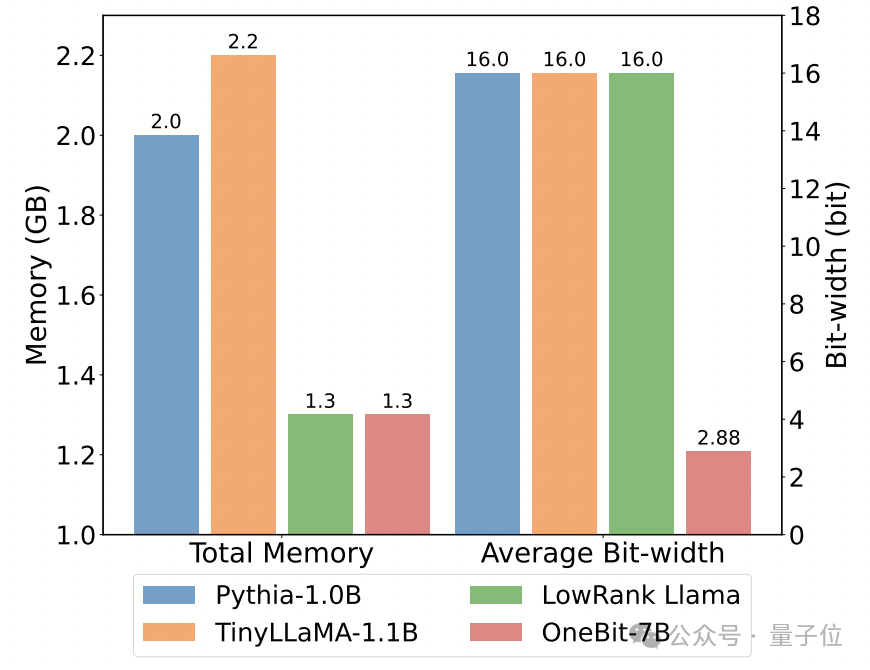
The author also compared the size and actual capabilities of several different types of small models.

The author found that although OneBit-7B has the smallest average bit width, takes up the smallest space, and requires relatively few training steps, it is not inferior to other models in terms of common sense reasoning capabilities.

At the same time, the author also found that the OneBit-7B model has serious knowledge forgetting in the field of social sciences.

△Comparison of FP16 linear layer and OneBit linear layer An example of text generation after fine-tuning of OneBit-7B instructions

The above picture also shows a OneBit- Text generation example after fine-tuning the 7B instruction. It can be seen that OneBit-7B has effectively gained the ability of the SFT stage and can generate text relatively smoothly, although the total parameters are only 1.3GB (comparable to the 0.6B model of FP16). Overall, OneBit-7B demonstrates its practical application value.

Analysis and Discussion

The author shows the compression ratio of OneBit for LLaMA models of different sizes. It can be seen that the compression ratio of OneBit for the model exceeds an astonishing 90%.

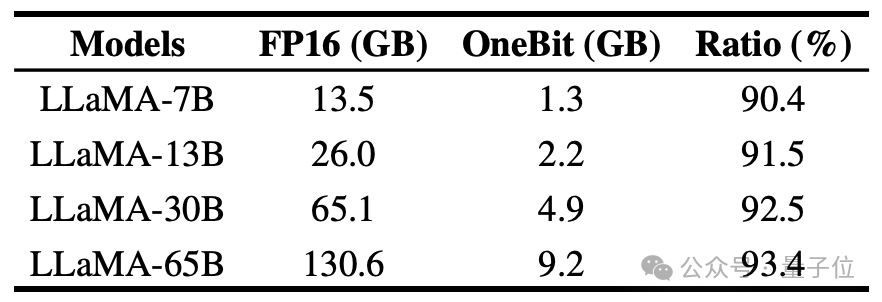
#In particular, as the model increases, the compression ratio of OneBit becomes higher.

This shows the advantage of the author's method on larger models: greater marginal gain (perplexity) at a higher compression ratio. Furthermore, the authors' approach achieves a good trade-off between size and performance.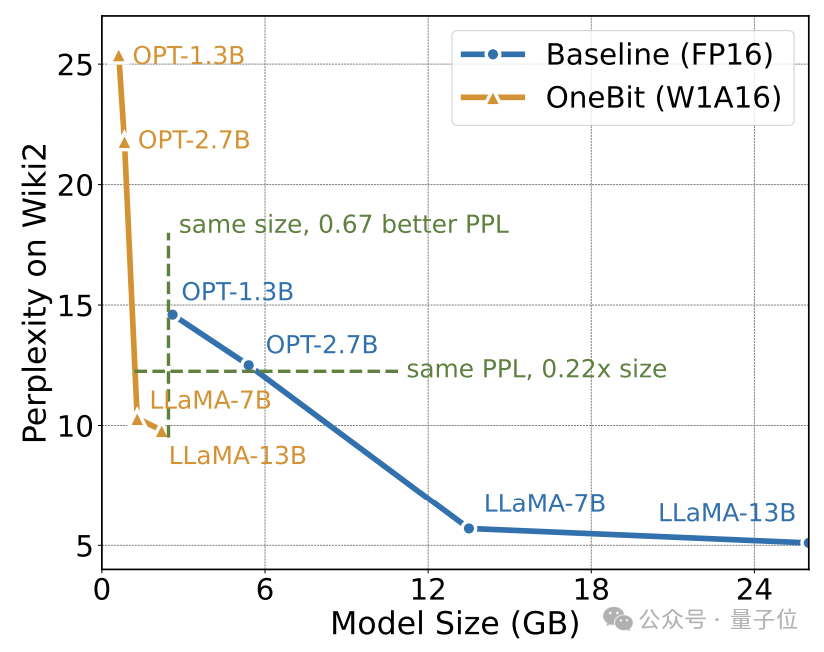

1bit quantitative model has computational advantages and is of great significance. The pure binary representation of parameters can not only save a lot of space, but also reduce the hardware requirements of matrix multiplication.

The element multiplication of matrix multiplication in high-precision models can be turned into efficient bit operations. Matrix products can be completed with only bit assignments and additions, which has great application prospects.

In addition, the author's method maintains excellent stable learning capabilities during the training process.

In fact, the instability problems, sensitivity to hyperparameters and convergence difficulties of binary network training have always been concerned by researchers.

The author analyzes the importance of high-precision value vectors in promoting stable convergence of the model.

Previous work has proposed a 1-bit model architecture and used it to train models from scratch (such as BitNet [1]), but it is sensitive to hyperparameters and difficult to transfer learning from a fully trained high-precision model. The author also tried BitNet's performance in knowledge distillation and found that its training was not stable enough.

Summary

The author proposed a model structure for 1-bit weight quantization and the corresponding parameter initialization method.

Extensive experiments on models of various sizes and series show that OneBit has clear advantages on representative strong baselines and achieves a good trade-off between model size and performance.

In addition, the author further analyzes the capabilities and prospects of this extremely low-bit quantization model and provides guidance for future research.

Paper address: https://arxiv.org/pdf/2402.11295.pdf

The above is the detailed content of Make large models 'slim down' by 90%! Tsinghua University & Harbin Institute of Technology proposed an extreme compression solution: 1-bit quantization, while retaining 83% of the capacity. For more information, please follow other related articles on the PHP Chinese website!