 Technology peripherals
Technology peripherals
 AI
AI
 A new breakthrough was made in the minimum cut problem of undirected graphs, and Google research won the SODA 2024 Best Paper Award
A new breakthrough was made in the minimum cut problem of undirected graphs, and Google research won the SODA 2024 Best Paper Award
A new breakthrough was made in the minimum cut problem of undirected graphs, and Google research won the SODA 2024 Best Paper Award
Google blog released new research to solve the minimum cut problem of undirected graphs.

Paper address: https://arxiv.org/pdf/2401.05627.pdf Paper Title: Deterministic Near-Linear Time Minimum Cut in Weighted Graphs
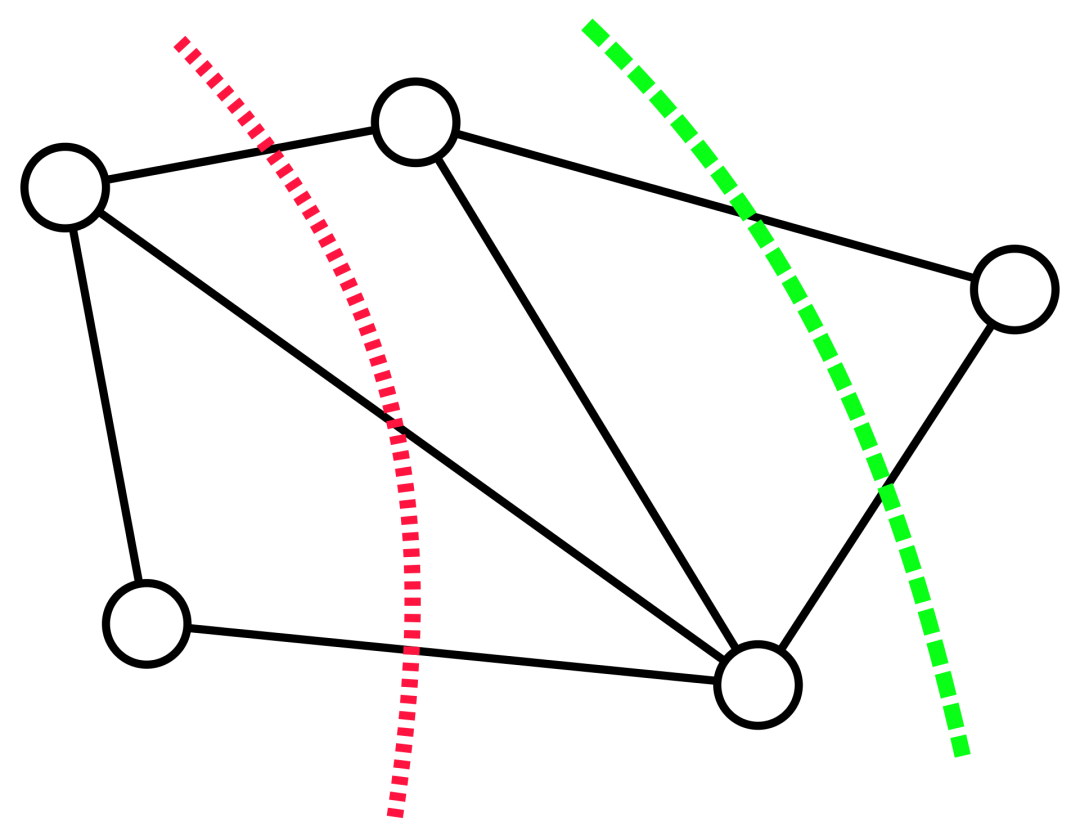
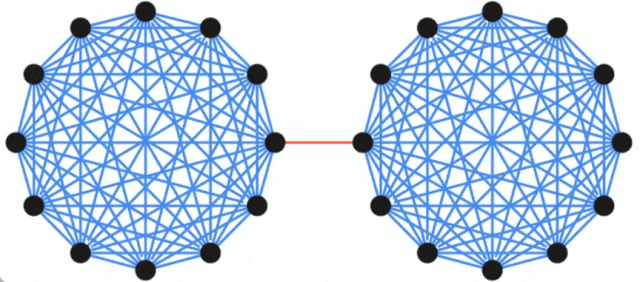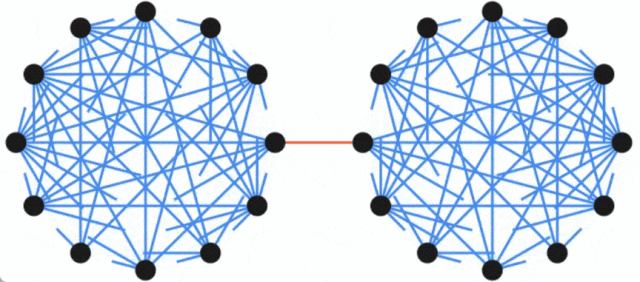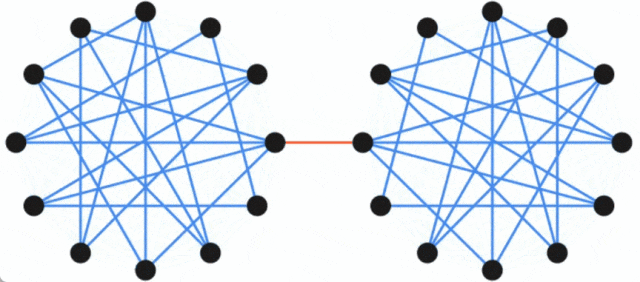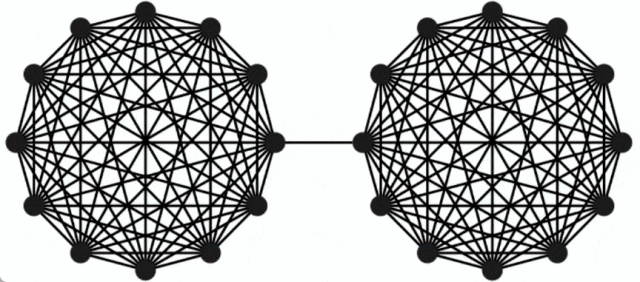
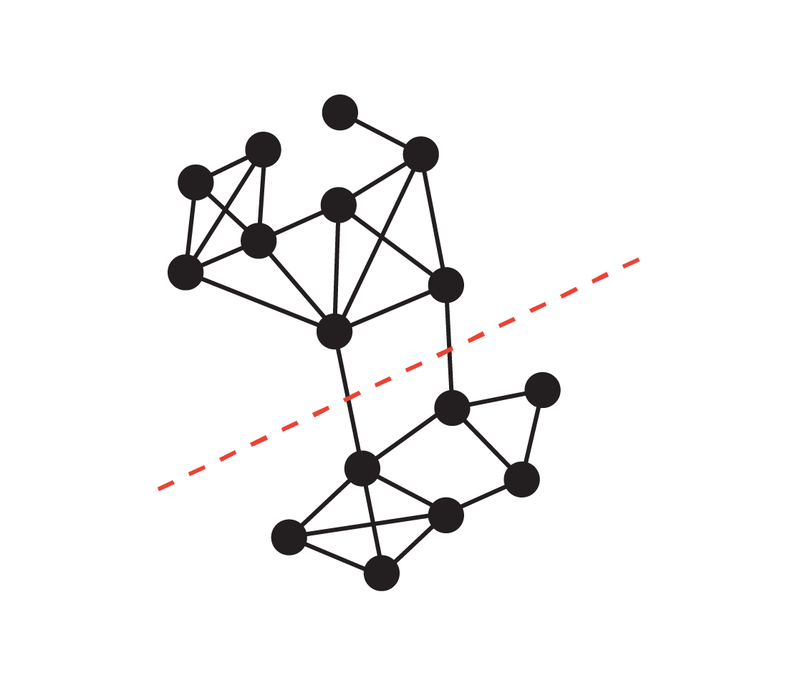
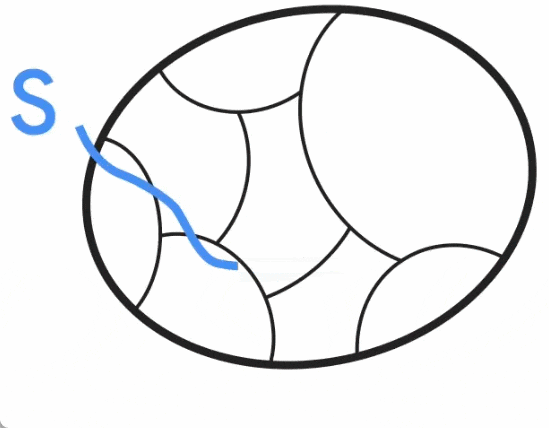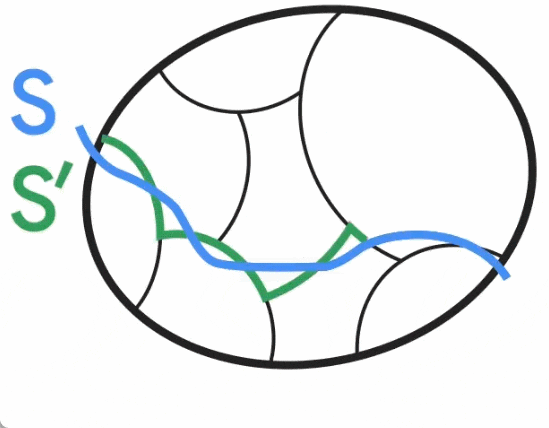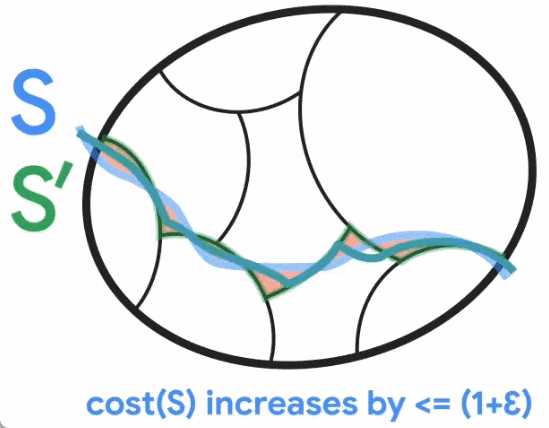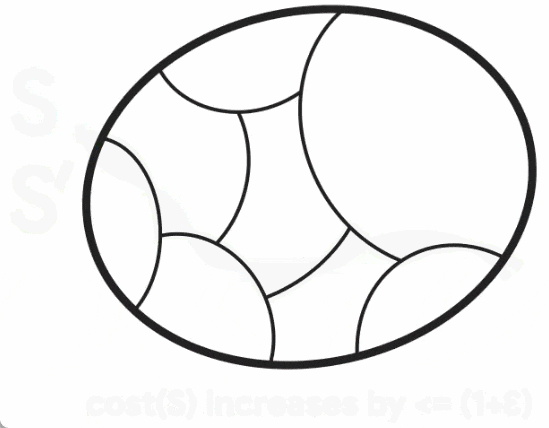
The above is the detailed content of A new breakthrough was made in the minimum cut problem of undirected graphs, and Google research won the SODA 2024 Best Paper Award. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1385
1385
 52
52
 How to comment deepseek
Feb 19, 2025 pm 05:42 PM
How to comment deepseek
Feb 19, 2025 pm 05:42 PM
DeepSeek is a powerful information retrieval tool. Its advantage is that it can deeply mine information, but its disadvantages are that it is slow, the result presentation method is simple, and the database coverage is limited. It needs to be weighed according to specific needs.
 How to search deepseek
Feb 19, 2025 pm 05:39 PM
How to search deepseek
Feb 19, 2025 pm 05:39 PM
DeepSeek is a proprietary search engine that only searches in a specific database or system, faster and more accurate. When using it, users are advised to read the document, try different search strategies, seek help and feedback on the user experience in order to make the most of their advantages.
 Sesame Open Door Exchange Web Page Registration Link Gate Trading App Registration Website Latest
Feb 28, 2025 am 11:06 AM
Sesame Open Door Exchange Web Page Registration Link Gate Trading App Registration Website Latest
Feb 28, 2025 am 11:06 AM
This article introduces the registration process of the Sesame Open Exchange (Gate.io) web version and the Gate trading app in detail. Whether it is web registration or app registration, you need to visit the official website or app store to download the genuine app, then fill in the user name, password, email, mobile phone number and other information, and complete email or mobile phone verification.
 Why can't the Bybit exchange link be directly downloaded and installed?
Feb 21, 2025 pm 10:57 PM
Why can't the Bybit exchange link be directly downloaded and installed?
Feb 21, 2025 pm 10:57 PM
Why can’t the Bybit exchange link be directly downloaded and installed? Bybit is a cryptocurrency exchange that provides trading services to users. The exchange's mobile apps cannot be downloaded directly through AppStore or GooglePlay for the following reasons: 1. App Store policy restricts Apple and Google from having strict requirements on the types of applications allowed in the app store. Cryptocurrency exchange applications often do not meet these requirements because they involve financial services and require specific regulations and security standards. 2. Laws and regulations Compliance In many countries, activities related to cryptocurrency transactions are regulated or restricted. To comply with these regulations, Bybit Application can only be used through official websites or other authorized channels
 Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download Address
Feb 28, 2025 am 10:51 AM
Sesame Open Door Trading Platform Download Mobile Version Gateio Trading Platform Download Address
Feb 28, 2025 am 10:51 AM
It is crucial to choose a formal channel to download the app and ensure the safety of your account.
 Top 10 recommended for crypto digital asset trading APP (2025 global ranking)
Mar 18, 2025 pm 12:15 PM
Top 10 recommended for crypto digital asset trading APP (2025 global ranking)
Mar 18, 2025 pm 12:15 PM
This article recommends the top ten cryptocurrency trading platforms worth paying attention to, including Binance, OKX, Gate.io, BitFlyer, KuCoin, Bybit, Coinbase Pro, Kraken, BYDFi and XBIT decentralized exchanges. These platforms have their own advantages in terms of transaction currency quantity, transaction type, security, compliance, and special features. For example, Binance is known for its largest transaction volume and abundant functions in the world, while BitFlyer attracts Asian users with its Japanese Financial Hall license and high security. Choosing a suitable platform requires comprehensive consideration based on your own trading experience, risk tolerance and investment preferences. Hope this article helps you find the best suit for yourself
 Sesame Open Door Exchange Web Page Login Latest version gateio official website entrance
Mar 04, 2025 pm 11:48 PM
Sesame Open Door Exchange Web Page Login Latest version gateio official website entrance
Mar 04, 2025 pm 11:48 PM
A detailed introduction to the login operation of the Sesame Open Exchange web version, including login steps and password recovery process. It also provides solutions to common problems such as login failure, unable to open the page, and unable to receive verification codes to help you log in to the platform smoothly.
 Binance binance official website latest version login portal
Feb 21, 2025 pm 05:42 PM
Binance binance official website latest version login portal
Feb 21, 2025 pm 05:42 PM
To access the latest version of Binance website login portal, just follow these simple steps. Go to the official website and click the "Login" button in the upper right corner. Select your existing login method. If you are a new user, please "Register". Enter your registered mobile number or email and password and complete authentication (such as mobile verification code or Google Authenticator). After successful verification, you can access the latest version of Binance official website login portal.



