Identify overfitting and underfitting through learning curves

This article will introduce how to effectively identify overfitting and underfitting in machine learning models through learning curves.

Underfitting and overfitting

1. Overfitting

If a model is overtrained on data to the point that it learns noise from it, the model is said to be overfitted. An overfitted model learns every example so perfectly that it will misclassify an unseen/new example. For an overfitted model, we will get a perfect/near-perfect training set score and a terrible validation set/test score.

Slightly modified: "The reason for overfitting: Use a complex model to solve a simple problem and extract noise from the data. Because a small data set may not be used as a training set Represents the correct representation of all data. "

2. Underfitting

If a model cannot correctly learn the patterns in the data, we Let's just say it's underfitting. Underfitting models do not fully learn every example in the data set. In this case, we see that the errors on both the training and validation sets are low. This may be because the model is too simple and does not have enough parameters to fit the data. We can try to increase the complexity of the model, increase the number of layers or neurons, to solve the under-fitting problem. However, it should be noted that increasing model complexity also increases the risk of overfitting.

Reasons why it is not suitable: Using a simple model to solve a complex problem, the model cannot learn all the patterns in the data, or the model incorrectly learns the patterns of the underlying data. In data analysis and machine learning, model selection is very important. Choosing the right model for your problem can improve the accuracy and reliability of your predictions. For complex problems, more complex models may be needed to capture all patterns in the data. In addition, you also need to consider the

learning curve

The learning curve draws the training sum of the training sample itself by incrementally adding new training samples. Verification loss. Can help us determine if we need to add additional training examples to improve the validation score (score on unseen data). If the model is overfitted, then adding additional training examples may improve the model's performance on unseen data. Likewise, if a model is underfit, then adding training examples may not be useful. The 'learning_curve' method can be imported from Scikit-Learn's 'model_selection' module.

from sklearn.model_selection import learning_curve

We will demonstrate using logistic regression and Iris data. Create a function called "learn_curve" that will fit a logistic regression model and return cross-validation scores, training scores, and learning curve data.

#The function below builds the model and returns cross validation scores, train score and learning curve data def learn_curve(X,y,c): ''' param X: Matrix of input featuresparam y: Vector of Target/Labelc: Inverse Regularization variable to control overfitting (high value causes overfitting, low value causes underfitting)''' '''We aren't splitting the data into train and test because we will use StratifiedKFoldCV.KFold CV is a preferred method compared to hold out CV, since the model is tested on all the examples.Hold out CV is preferred when the model takes too long to train and we have a huge test set that truly represents the universe'''  le = LabelEncoder() # Label encoding the target sc = StandardScaler() # Scaling the input features y = le.fit_transform(y)#Label Encoding the target log_reg = LogisticRegression(max_iter=200,random_state=11,C=c) # LogisticRegression model # Pipeline with scaling and classification as steps, must use a pipelne since we are using KFoldCV lr = Pipeline(steps=(['scaler',sc],['classifier',log_reg]))   cv = StratifiedKFold(n_splits=5,random_state=11,shuffle=True) # Creating a StratifiedKFold object with 5 folds cv_scores = cross_val_score(lr,X,y,scoring="accuracy",cv=cv) # Storing the CV scores (accuracy) of each fold   lr.fit(X,y) # Fitting the model  train_score = lr.score(X,y) # Scoring the model on train set  #Building the learning curve train_size,train_scores,test_scores =learning_curve(estimator=lr,X=X,y=y,cv=cv,scoring="accuracy",random_state=11) train_scores = 1-np.mean(train_scores,axis=1)#converting the accuracy score to misclassification rate test_scores = 1-np.mean(test_scores,axis=1)#converting the accuracy score to misclassification rate lc =pd.DataFrame({"Training_size":train_size,"Training_loss":train_scores,"Validation_loss":test_scores}).melt(id_vars="Training_size") return {"cv_scores":cv_scores,"train_score":train_score,"learning_curve":lc}

The above code is very simple, it is our daily training process. Now we start to introduce the use of learning curve

1. Learning curve of the fitted model

We will use the 'learn_curve' function to obtain a good fitted model by setting the anti-regularization variable/parameter 'c' to 1 (i.e. we don't perform any regularization).

lc = learn_curve(X,y,1) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Deep HUB Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])}\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of Good Fit Model") plt.ylabel("Misclassification Rate/Loss");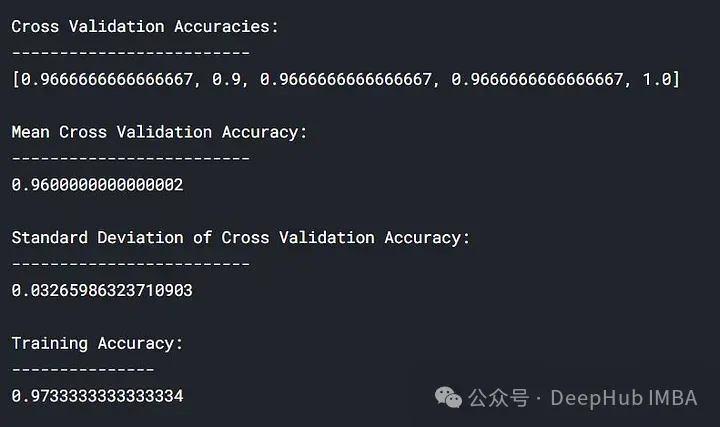

#In the above results, the cross-validation accuracy is close to the training accuracy.

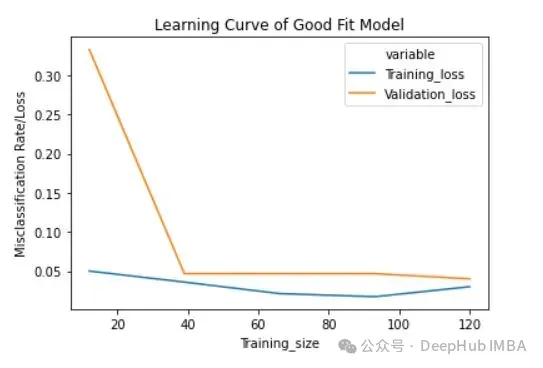
Training loss (blue): The learning curve of a good fitted model will gradually decrease and decrease as the number of training examples increases. It gradually becomes flat, indicating that adding more training examples does not improve the model's performance on the training data.

Validation loss (yellow): The learning curve of a well-fitted model has a high validation loss at the beginning, which gradually decreases and gradually decreases as the number of training examples increases. tends to be flat, indicating that the more samples, the more patterns can be learned. These patterns will be helpful for "unseen" data

Finally, you can also see that in After adding a reasonable number of training examples, the training loss and validation loss approach each other.

2. Learning Curve of Overfitting Model

We will use the 'learn_curve' function by deregularizing the variable/parameter 'c 'Set to 10000 to get an overfitted model (high values ​​of 'c' result in overfitting).

lc = learn_curve(X,y,10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Deep HUB Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (High Variance)\n\n\ Training Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Overfit Model") plt.ylabel("Misclassification Rate/Loss");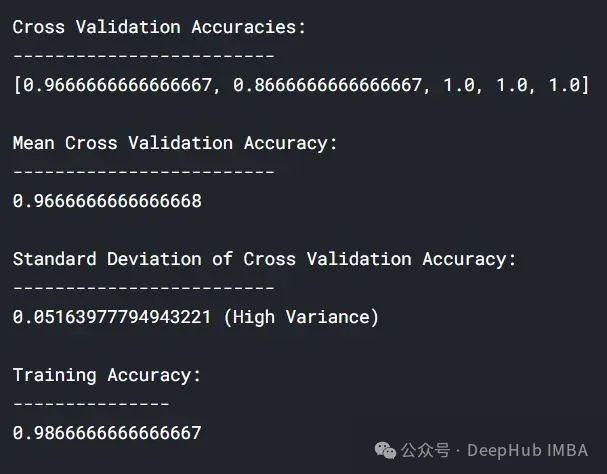

与拟合模型相比，交叉验证精度的标准差较高。

过拟合模型的学习曲线一开始的训练损失很低，随着训练样例的增加，学习曲线逐渐增加，但不会变平。过拟合模型的学习曲线在开始时具有较高的验证损失，随着训练样例的增加逐渐减小并且不趋于平坦，说明增加更多的训练样例可以提高模型在未知数据上的性能。同时还可以看到，训练损失和验证损失彼此相差很远，在增加额外的训练数据时，它们可能会彼此接近。

3、欠拟合模型的学习曲线

将反正则化变量/参数' c '设置为1/10000来获得欠拟合模型(' c '的低值导致欠拟合)。

lc = learn_curve(X,y,1/10000) print(f'Cross Validation Accuracies:\n{"-"*25}\n{list(lc["cv_scores"])}\n\n\ Mean Cross Validation Accuracy:\n{"-"*25}\n{np.mean(lc["cv_scores"])}\n\n\ Standard Deviation of Cross Validation Accuracy:\n{"-"*25}\n{np.std(lc["cv_scores"])} (Low variance)\n\n\ Training Deep HUB Accuracy:\n{"-"*15}\n{lc["train_score"]}\n\n') sns.lineplot(data=lc["learning_curve"],x="Training_size",y="value",hue="variable") plt.title("Learning Curve of an Underfit Model") plt.ylabel("Misclassification Rate/Loss");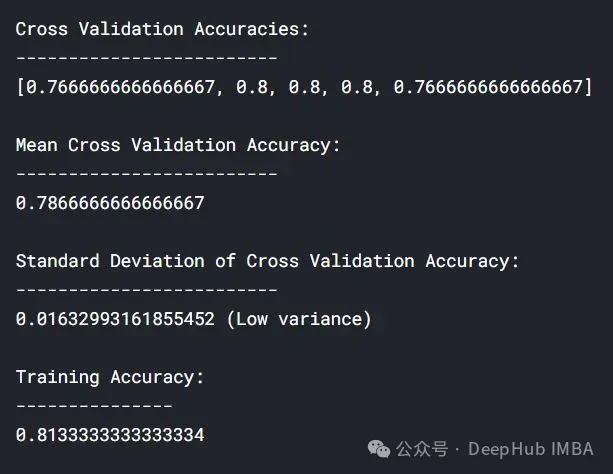

与过拟合和良好拟合模型相比，交叉验证精度的标准差较低。

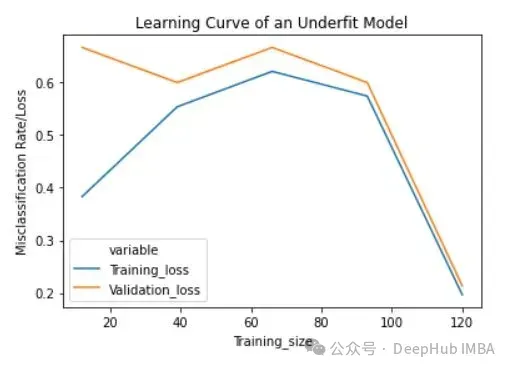
欠拟合模型的学习曲线在开始时具有较低的训练损失，随着训练样例的增加逐渐增加，并在最后突然下降到任意最小点(最小并不意味着零损失)。这种最后的突然下跌可能并不总是会发生。这表明增加更多的训练样例并不能提高模型在未知数据上的性能。

总结

在机器学习和统计建模中，过拟合（Overfitting）和欠拟合（Underfitting）是两种常见的问题，它们描述了模型与训练数据的拟合程度如何影响模型在新数据上的表现。

分析生成的学习曲线时，可以关注以下几个方面：

• 欠拟合：如果学习曲线显示训练集和验证集的性能都比较低，或者两者都随着训练样本数量的增加而缓慢提升，这通常表明模型欠拟合。这种情况下，模型可能太简单，无法捕捉数据中的基本模式。
• 过拟合：如果训练集的性能随着样本数量的增加而提高，而验证集的性能在一定点后开始下降或停滞不前，这通常表示模型过拟合。在这种情况下，模型可能太复杂，过度适应了训练数据中的噪声而非潜在的数据模式。

根据学习曲线的分析，你可以采取以下策略进行调整：

• 对于欠拟合：

• 增加模型复杂度，例如使用更多的特征、更深的网络或更多的参数。
• 改善特征工程，尝试不同的特征组合或转换。
• 增加迭代次数或调整学习率。

• 对于过拟合：

• 使用正则化技术（如L1、L2正则化）。

• 减少模型的复杂性，比如减少参数数量、层数或特征数量。

• 增加更多的训练数据。

• 应用数据增强技术。

• 使用早停（early stopping）等技术来避免过度训练。

通过这样的分析和调整，学习曲线能够帮助你更有效地优化模型，并提高其在未知数据上的泛化能力。

The above is the detailed content of Identify overfitting and underfitting through learning curves. For more information, please follow other related articles on the PHP Chinese website!