Reversal after explosion? KAN who 'killed an MLP in one night': Actually, I am also an MLP

Multi-layer perceptron (MLP), also known as fully connected feed-forward neural network, is the basic building block of today's deep learning models. The importance of MLPs cannot be overstated, as they are the default method in machine learning for approximating nonlinear functions.

But recently, researchers from MIT and other institutions have proposed a very promising alternative method-KAN . This method outperforms MLP in terms of accuracy and interpretability. Furthermore, it is able to outperform MLPs run with a much larger number of parameters with a very small number of parameters. For example, the authors stated that they used KAN to rediscover the mathematical laws in knot theory and reproduce DeepMind's results with smaller networks and a higher degree of automation. Specifically, DeepMind's MLP has about 300,000 parameters, while KAN only has about 200 parameters.

The fine-tuning content is as follows: These amazing research results made KAN quickly become popular and attracted many people to study it. Soon, some people raised some doubts. Among them, a Colab document titled "KAN is just MLP" became the focus of discussion.

KAN JUST A REGULAR MLP?

The author of the above document stated that you can write KAN as an MLP by adding some repetitions and shifts before ReLU.

In a short example, the author shows how to rewrite the KAN network into a normal MLP with the same number of parameters and a slightly nonlinear structure.

What needs to be remembered is that KAN has activation functions on the edges. They use B-splines. In the examples shown, the authors will only use piece-wise linear functions for simplicity. This does not change the modeling capabilities of the network.

The following is an example of a piece-wise linear function:

def f(x):if x

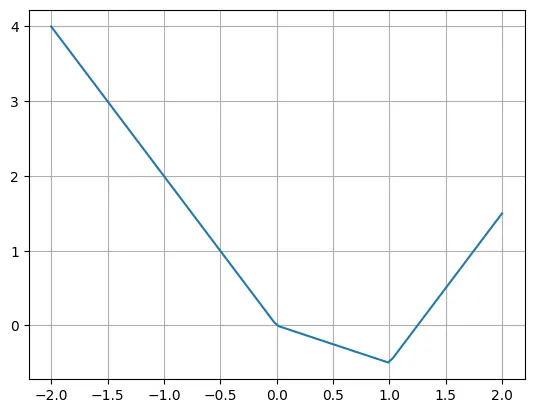
The author states that we can easily rewrite this function using multiple ReLU and linear functions. Note that sometimes it is necessary to move the input of ReLU.

plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)plt.grid()

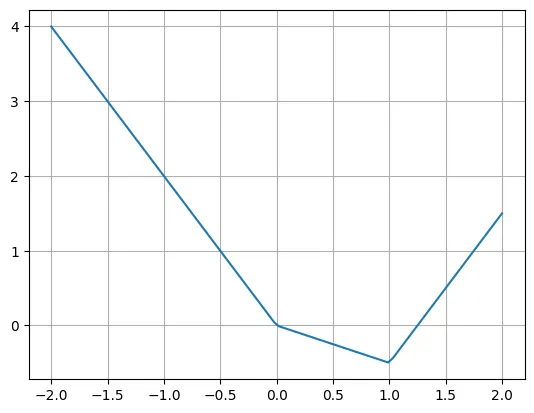
#The real question is how to rewrite the KAN layer into a typical MLP layer. Suppose there are n input neurons, m output neurons, and the piece-wise function has k pieces. This requires n*m*k parameters (k parameters per edge, and you have n*m ​​edges).

Now consider a KAN edge. To do this, the input needs to be copied k times, each copy shifted by a constant, and then run through ReLU and linear layers (except for the first layer). Graphically it looks like this (C is the constant and W is the weight):

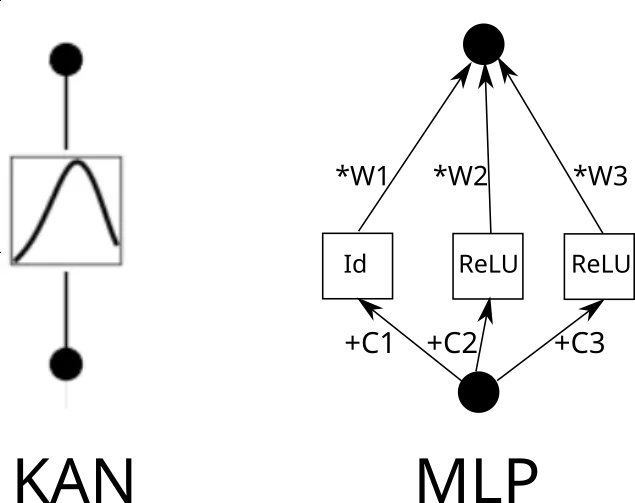
Now, you can repeat this process for each edge. But one thing to note is that if the piece-wise linear function grid is the same everywhere, we can share the intermediate ReLU output and just blend the weights on it. Like this:

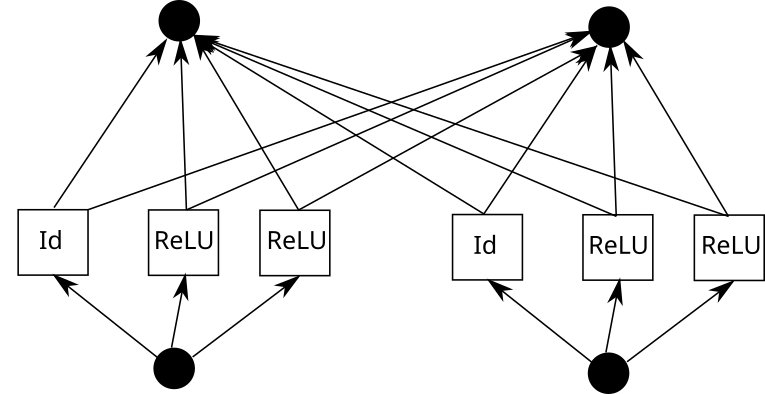
## In Pytorch, this translates to:

k = 3 # Grid sizeinp_size = 5out_size = 7batch_size = 10X = torch.randn(batch_size, inp_size) # Our inputlinear = nn.Linear(inp_size*k, out_size)# Weightsrepeated = X.unsqueeze(1).repeat(1,k,1)shifts = torch.linspace(-1, 1, k).reshape(1,k,1)shifted = repeated + shiftsintermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)outputs = linear(intermediate)

Now our layer looks like this:

• Expand shift ReLU
• Linear

Consider the three layers one after another:

• Expand shift ReLU (Layer 1 starts here)
• Linear
• Expand shift ReLU (Layer 2 starts here)
• Linear
• Expand shift ReLU (Layer 3 starts here)
• Linear

Ignore input expansion , we can rearrange:

• Linear (Layer 1 starts here)
• Expand shift ReLU
• Linear (Layer 2 starts here)
• Expand shift ReLU

The following layers are basically It can be called MLP. You can also make the linear layer larger and remove expand and shift to obtain better modeling capabilities (albeit at a higher parameter cost).

• Linear (Layer 2 starts here)
• Expand shift ReLU

Through this example, the author shows that KAN is a kind of MLP. This statement triggered everyone to rethink the two types of methods.

Re-examination of KAN ideas, methods and results

In fact, in addition to ignoring MLP KAN has also been questioned by many other parties over its relationship with the Qing Dynasty.

In summary, the researchers’ discussion mainly focused on the following points.

First, the main contribution of KAN lies in interpretability, not in expansion speed, accuracy, etc.

The author of the paper once said:

1. KAN expands faster than MLP. KAN has better accuracy than MLP with fewer parameters.
2. KAN can be visualized intuitively. KAN provides interpretability and interactivity that MLP cannot. We can potentially discover new scientific laws using KANs.

Among them, the importance of network interpretability for models to solve real-life problems is self-evident:

But the question is: "I think their claim is just that it learns faster and is interpretable, and nothing else. If KAN has much fewer parameters than the equivalent NN, then the former is Meaningful. I still feel that training KAN is very unstable. "

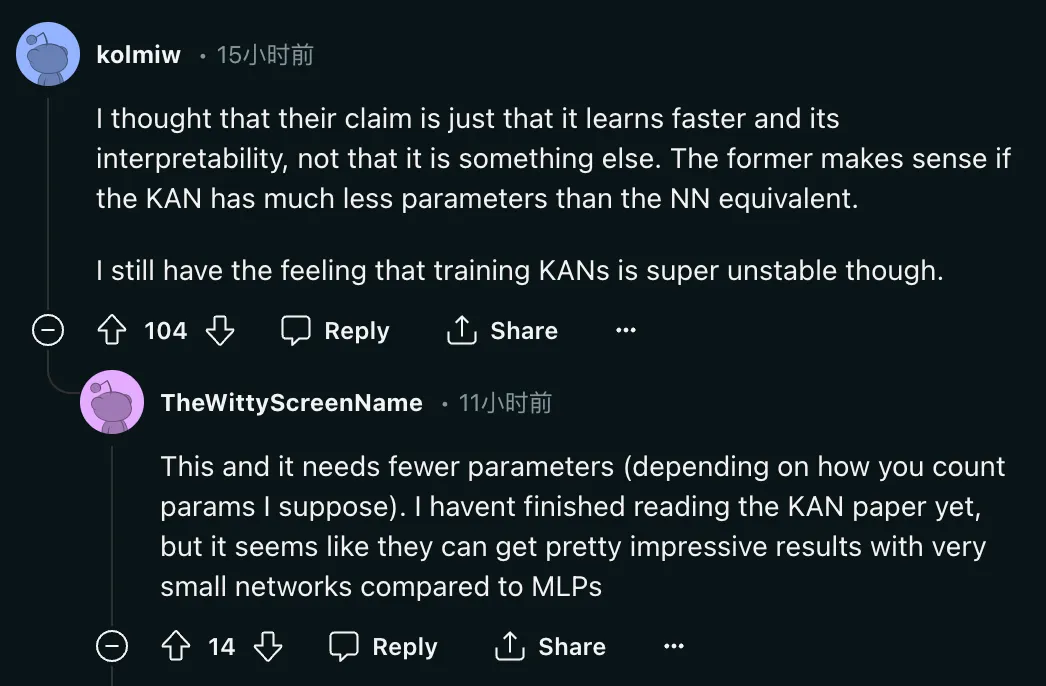
#So can KAN have much fewer parameters than the equivalent NN? ?

There are still doubts about this statement. In the paper, the authors of KAN stated that they were able to reproduce DeepMind's research on mathematical theorems using an MLP of 300,000 parameters using only 200 parameters of KAN. After seeing the results, two students of Georgia Tech associate professor Humphrey Shi re-examined DeepMind's experiments and found that with only 122 parameters, DeepMind's MLP could match KAN's 81.6% accuracy. Moreover, they did not make any major changes to the DeepMind code. To achieve this result, they only reduced the network size, used random seeds, and increased training time.

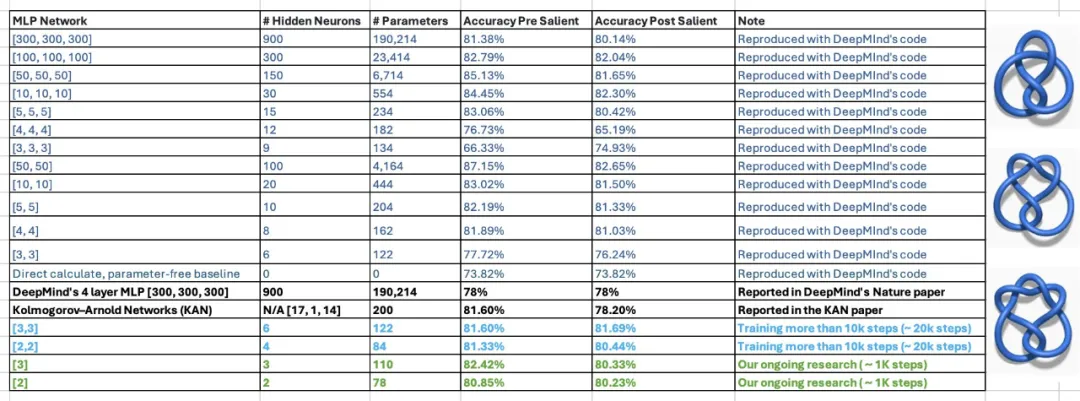
To this, the author of the paper also gave a positive response:

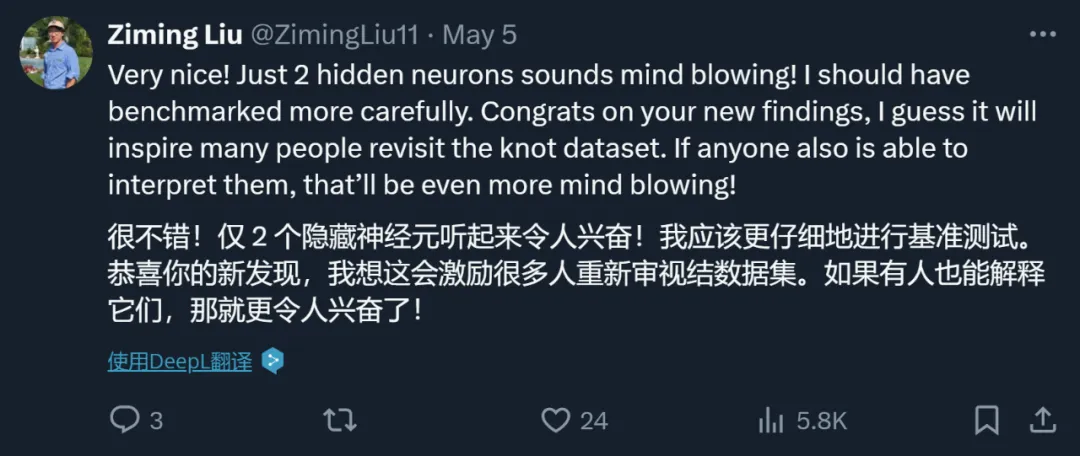
Second, KAN and MLP are not fundamentally different in approach.

"Yes, this is obviously the same thing. In KAN they do activation first and then linear combination, while in MLP they do linear combination first and then Then do the activation. Amplifying it is basically the same thing. As far as I know, the main reasons for using KAN are interpretability and symbolic regression. ##In addition to questioning the method, the researcher also called for a return to rationality in the evaluation of this paper:

"I think people need to stop treating the KAN paper as depth. A huge shift in learning the basic units and just treating it as a good paper on the interpretability of deep learning. The interpretability of the nonlinear functions learned on each edge is the main contribution of this paper."

##Third, some researchers said that KAN’s idea is not new.

"This was studied in the 1980s. A Hacker News discussion mentioned an Italian paper discussing this issue. So it’s nothing new at all. 40 years later, it’s just something that has either come back or been rejected and is being revisited.”

But what you can see is. , the authors of the KAN paper did not gloss over the issue either.

"These ideas are not new, but I don't think the author is shying away from that. He just packaged everything up nicely and did some nice work on the toy data Experiment. But it is also a contribution."

##At the same time, Ian Goodfellow and Yoshua Bengio's paper MaxOut (https://arxiv.org/pdf/ 1302.4389) has also been mentioned, and some researchers believe that the two "although slightly different, the ideas are somewhat similar."

Author: The original research goal was indeed interpretability

As a result of the heated discussion, one of the authors, Sachin Vaidya, came forward.

As one of the authors of this paper, I would like to say a few words. The attention KAN is receiving is amazing, and this discussion is exactly what is needed to push new technologies to their limits and find out what works and what doesn’t.

I thought I’d share some background on motivation. Our main idea for implementing KAN stems from our search for interpretable AI models that can "learn" the insights that physicists discover about natural laws. Therefore, as others have realized, we are entirely focused on this goal because traditional black-box models cannot provide insights critical to fundamental discoveries in science. We then show through examples related to physics and mathematics that KAN significantly outperforms traditional methods in terms of interpretability. We certainly hope that the usefulness of KAN will extend far beyond our initial motivations.

On the GitHub homepage, Liu Ziming, one of the authors of the paper, also responded to the evaluation of this research:

I was asked recently The most common question I get is whether KAN will become the next generation LLM. I don't have a clear judgment on this.

KAN is designed for applications that care about high accuracy and interpretability. We do care about the interpretability of LLMs, but interpretability can mean very different things for LLMs and science. Do we care about high accuracy of LLM? The scaling laws seem to imply so, but perhaps not very accurately. Furthermore, accuracy can also mean different things for LLM and science.

I welcome people to criticize KAN, practice is the only criterion for testing truth. There are many things we don’t know in advance until they are actually tried and proven to be a success or a failure. While I'd love to see KAN succeed, I'm equally curious about KAN's failure.

KAN and MLP are not substitutes for each other. They each have advantages in some situations and limitations in some situations. I would be interested in theoretical frameworks that encompass both, and maybe even come up with new alternatives (physicists love unified theories, sorry).

KAN The first author of the paper is Liu Ziming. He is a physicist and machine learning researcher and is currently a third-year PhD student at MIT and IAIFI under Max Tegmark. His research interests focus on the intersection of artificial intelligence and physics.

The above is the detailed content of Reversal after explosion? KAN who 'killed an MLP in one night': Actually, I am also an MLP. For more information, please follow other related articles on the PHP Chinese website!