Quantile regression for time series probabilistic forecasting
Do not change the meaning of the original content, fine-tune the content, rewrite the content, and do not continue writing. "Quantile regression meets this need, providing prediction intervals with quantified chances. It is a statistical technique used to model the relationship between a predictor variable and a response variable, especially when the conditional distribution of the response variable is of interest When. Unlike traditional regression methods, quantile regression focuses on estimating the conditional magnitude of the response variable rather than the conditional mean.”
 ##Figure (A): Quantile. Regression
##Figure (A): Quantile. Regression
!pip install neuralprophet!pip uninstall numpy!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5
%matplotlib inlinefrom matplotlib import pyplot as pltimport pandas as pdimport numpy as npimport loggingimport warningslogging.getLogger('prophet').setLevel(logging.ERROR)warnings.filterwarnings("ignore")data = pd.read_csv('/bike_sharing_daily.csv')data.tail() Picture (B): Shared bicycles
Picture (B): Shared bicycles
# convert string to datetime64data["ds"] = pd.to_datetime(data["dteday"])# create line plot of sales dataplt.plot(data['ds'], data["cnt"])plt.xlabel("date")plt.ylabel("Count")plt.show()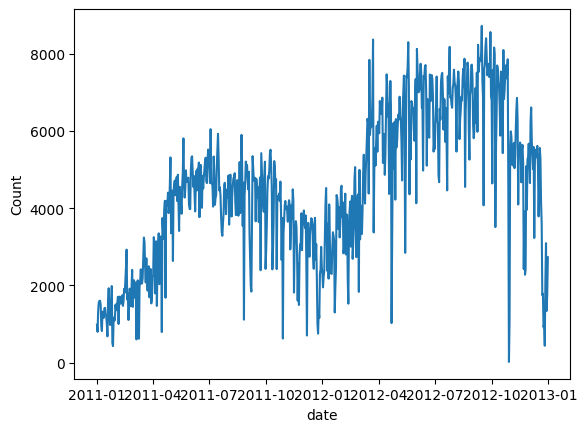 Figure (C): Daily demand for bicycle rental
Figure (C): Daily demand for bicycle rental
df = data[['ds','cnt']]df.columns = ['ds','y']
构建分位数回归模型
直接在 NeuralProphet 中构建分位数回归。假设我们需要第 5、10、50、90 和 95 个量级的值。我们指定 quantile_list = [0.05,0.1,0.5,0.9,0.95],并打开参数 quantiles = quantile_list。
from neuralprophet import NeuralProphet, set_log_levelquantile_list=[0.05,0.1,0.5,0.9,0.95 ]# Model and predictionm = NeuralProphet(quantiles=quantile_list,yearly_seasnotallow=True,weekly_seasnotallow=True,daily_seasnotallow=False)m = m.add_country_holidays("US")m.set_plotting_backend("matplotlib")# Use matplotlibdf_train, df_test = m.split_df(df, valid_p=0.2)metrics = m.fit(df_train, validation_df=df_test, progress="bar")metrics.tail()分位数回归预测
我们将使用 .make_future_dataframe()为预测创建新数据帧,NeuralProphet 是基于 Prophet 的。参数 n_historic_predictions 为 100,只包含过去的 100 个数据点。如果设置为 True,则包括整个历史数据。我们设置 period=50 来预测未来 50 个数据点。
future = m.make_future_dataframe(df, periods=50, n_historic_predictinotallow=100) #, n_historic_predictinotallow=1)# Perform prediction with the trained modelsforecast = m.predict(df=future)forecast.tail(60)
预测结果存储在数据框架 predict 中。
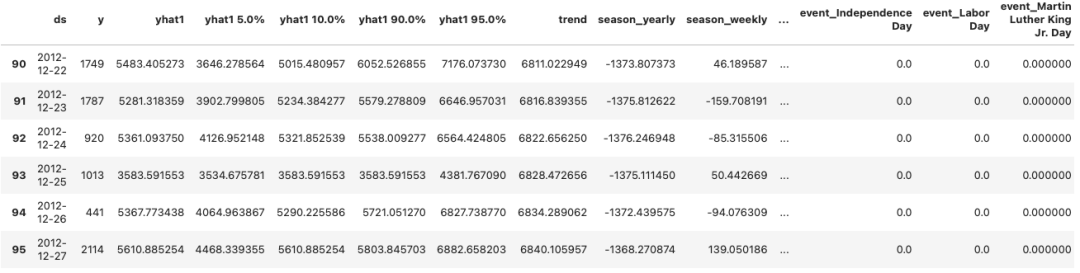 图 (D):预测
图 (D):预测
上述数据框架包含了绘制地图所需的所有数据元素。
m.plot(forecast, plotting_backend="plotly-static"#plotting_backend = "matplotlib")
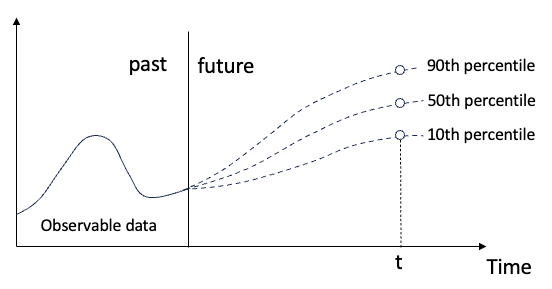
预测区间是由分位数值提供的!
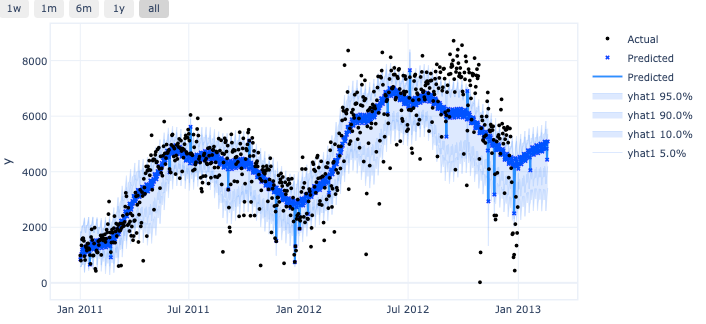 图 (E):分位数预测
图 (E):分位数预测
预测区间和置信区间的区别
预测区间和置信区间在流行趋势中很有帮助,因为它们可以量化不确定性。它们的目标、计算方法和应用是不同的。下面我将用回归来解释两者的区别。在图(F)中,我在左边画出了线性回归,在右边画出了分位数回归。
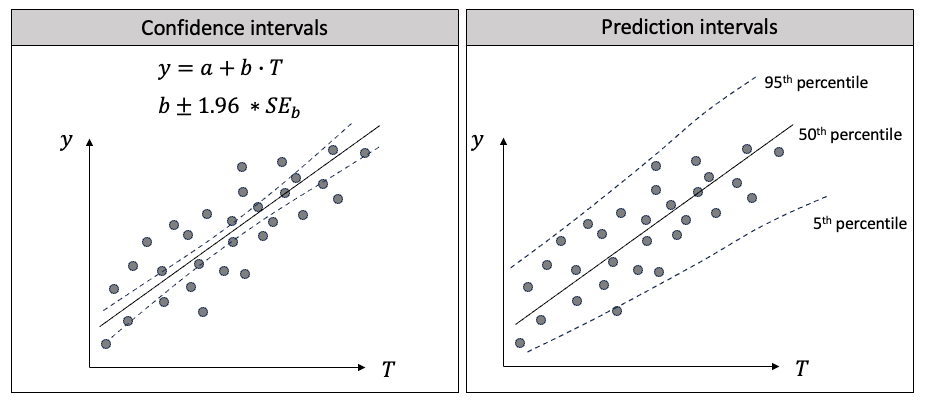 图(F):置信区间与预测区间的区别
图(F):置信区间与预测区间的区别
首先,它们的目标不同:
- 线性回归的主要目标是找到一条线,使预测值尽可能接近给定自变量值时因变量的条件均值。
- 分位数回归旨在提供未来观测值的范围,在一定的置信度下。它估计自变量与因变量条件分布的不同量化值之间的关系。
其次,它们的计算方法不同:
- 在线性回归中,置信区间是对自变量系数的区间估计,通常使用普通最小二乘法 (OLS) 找出数据点到直线的最小总距离。系数的变化会影响预测的条件均值 Y。
- 在分位数回归中,你可以选择依赖变量的不同量级来估计回归系数,通常是最小化绝对偏差的加权和,而不是使用OLS方法。
第三,它们的应用不同:
- 在线性回归中,预测的条件均值有 95% 的置信区间。置信区间较窄,因为它是条件平均值,而不是整个范围。
- 在分位数回归中,预测值有 95% 的概率落在预测区间的范围内。
写在最后
本文介绍了分位数回归预测区间的概念,以及如何利用 NeuralProphet 生成预测区间。我们还强调了预测区间和置信区间之间的差异,这在商业应用中经常引起混淆。后面将继续探讨另一项重要的技术,即复合分位数回归(CQR),用于预测不确定性。
The above is the detailed content of Quantile regression for time series probabilistic forecasting. For more information, please follow other related articles on the PHP Chinese website!

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1378
1378
 52
52
 How to run the h5 project
Apr 06, 2025 pm 12:21 PM
How to run the h5 project
Apr 06, 2025 pm 12:21 PM
Running the H5 project requires the following steps: installing necessary tools such as web server, Node.js, development tools, etc. Build a development environment, create project folders, initialize projects, and write code. Start the development server and run the command using the command line. Preview the project in your browser and enter the development server URL. Publish projects, optimize code, deploy projects, and set up web server configuration.
 Gitee Pages static website deployment failed: How to troubleshoot and resolve single file 404 errors?
Apr 04, 2025 pm 11:54 PM
Gitee Pages static website deployment failed: How to troubleshoot and resolve single file 404 errors?
Apr 04, 2025 pm 11:54 PM
GiteePages static website deployment failed: 404 error troubleshooting and resolution when using Gitee...
 Does H5 page production require continuous maintenance?
Apr 05, 2025 pm 11:27 PM
Does H5 page production require continuous maintenance?
Apr 05, 2025 pm 11:27 PM
The H5 page needs to be maintained continuously, because of factors such as code vulnerabilities, browser compatibility, performance optimization, security updates and user experience improvements. Effective maintenance methods include establishing a complete testing system, using version control tools, regularly monitoring page performance, collecting user feedback and formulating maintenance plans.
 How to quickly build a foreground page in a React Vite project using AI tools?
Apr 04, 2025 pm 01:45 PM
How to quickly build a foreground page in a React Vite project using AI tools?
Apr 04, 2025 pm 01:45 PM
How to quickly build a front-end page in back-end development? As a backend developer with three or four years of experience, he has mastered the basic JavaScript, CSS and HTML...
 Can you learn how to make H5 pages by yourself?
Apr 06, 2025 am 06:36 AM
Can you learn how to make H5 pages by yourself?
Apr 06, 2025 am 06:36 AM
It is feasible to self-study H5 page production, but it is not a quick success. It requires mastering HTML, CSS, and JavaScript, involving design, front-end development, and back-end interaction logic. Practice is the key, and learn by completing tutorials, reviewing materials, and participating in open source projects. Performance optimization is also important, requiring optimization of images, reducing HTTP requests and using appropriate frameworks. The road to self-study is long and requires continuous learning and communication.
 How to use vue pagination
Apr 08, 2025 am 06:45 AM
How to use vue pagination
Apr 08, 2025 am 06:45 AM
Pagination is a technology that splits large data sets into small pages to improve performance and user experience. In Vue, you can use the following built-in method to paging: Calculate the total number of pages: totalPages() traversal page number: v-for directive to set the current page: currentPage Get the current page data: currentPageData()
 How to view the results after Bootstrap is modified
Apr 07, 2025 am 10:03 AM
How to view the results after Bootstrap is modified
Apr 07, 2025 am 10:03 AM
Steps to view modified Bootstrap results: Open the HTML file directly in the browser to ensure that the Bootstrap file is referenced correctly. Clear the browser cache (Ctrl Shift R). If you use CDN, you can directly modify CSS in the developer tool to view the effects in real time. If you modify the Bootstrap source code, download and replace the local file, or rerun the build command using a build tool such as Webpack.
 HadiDB: A lightweight, horizontally scalable database in Python
Apr 08, 2025 pm 06:12 PM
HadiDB: A lightweight, horizontally scalable database in Python
Apr 08, 2025 pm 06:12 PM
HadiDB: A lightweight, high-level scalable Python database HadiDB (hadidb) is a lightweight database written in Python, with a high level of scalability. Install HadiDB using pip installation: pipinstallhadidb User Management Create user: createuser() method to create a new user. The authentication() method authenticates the user's identity. fromhadidb.operationimportuseruser_obj=user("admin","admin")user_obj.




