 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 Detailed explanation of JavaScript data structure and algorithm stack_javascript skills
Detailed explanation of JavaScript data structure and algorithm stack_javascript skills
Detailed explanation of JavaScript data structure and algorithm stack_javascript skills
In the previous article the blog introduced the following list. The list is the simplest structure, but if you want to deal with some more complex structures, the list is too simple, so we need some kind of and Lists are similar to but more complex data structures - stacks. The stack is an efficient data structure because data can only be added or deleted at the top of the stack, so this operation is fast and easy to implement.
1: Operations on the stack.
The stack is a special kind of list. The elements in the stack can only be accessed through one end of the list, which is the top of the stack. For example, when washing dishes in a restaurant, you can only wash the top plate first. After the plate is washed, it can only be screwed to the top of the pile of plates. The stack is a data structure called "last in, first out" (LIFO).
Since the stack has the last-in-first-out characteristic, any element that is not at the top of the stack cannot be accessed. In order to get the element at the bottom of the stack, the element above must be removed first. The two main operations we can perform on the stack are pushing an element onto the stack and popping an element off the stack. We can use the push() method to push into the stack, and the pop() method to pop out of the stack. Although the pop() method can access the element on the top of the stack, after calling this method, the element on the top of the stack is permanently deleted from the stack. Another commonly used method is peek(), which only returns the top element of the stack without deleting it.
The actual diagram of pushing and popping onto the stack is as follows:
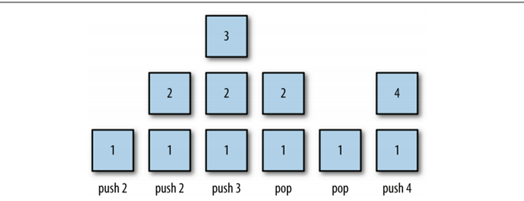
push(), pop() and peek() are the three main methods of the stack, but the stack has other methods and properties. As follows:
clear(): Clear all elements in the stack.
length(): Record the number of elements in the stack.
2: The implementation of the stack is as follows:
We can start by implementing the methods of the stack class; as follows:
function Stack() {
This.dataStore = [];
This.top = 0;
}
As above: dataStore saves all elements in the stack. The variable top records the position of the top of the stack and is initialized to 0. It means that the starting position of the array corresponding to the top of the stack is 0, if an element is pushed onto the stack. The variable value will change accordingly.
We also have the following methods: push(), pop(), peek(), clear(), length();
1. Push() method; when pushing a new element into the stack, it needs to be saved in the position corresponding to the variable top in the array, and then the top value is increased by 1 to point to the next position in the array. The following code:
function push(element) {
This.dataStore[this.top] = element;
}
2. The pop() method is the opposite of the push() method---it returns the top element of the stack and decrements the top value by 1. The following code:
function pop(){
return this.dataStore[--this.top];
}
3. The peek() method returns the element at the top-1 position of the array, which is the top element of the stack;
Function peek(){
return this.dataStore[this.top - 1];
}
4. length() method Sometimes we need to know how many elements there are in the stack. We can return the number of elements in the stack by returning the value of the variable top, as shown in the following code:
Function length(){
return this.top;
}
5. clear(); Sometimes we want to clear the stack, we set the variable top value to 0; the following code:
function clear() {
this.top = 0;
}
All codes below:
function Stack() {
This.dataStore = [];
This.top = 0;
}
Stack.prototype = {
//Push a new element into the stack
Push: function(element) {
This.dataStore[this.top] = element;
},
// Access the top element of the stack, the top element of the stack is permanently deleted
pop: function(){
return this.dataStore[--this.top];
},
// Return the element at the top-1 position in the array, that is, the top element of the stack
peek: function(){
return this.dataStore[this.top - 1];
},
//How many elements are stored in the stack
length: function(){
return this.top;
},
//Clear the stack
; clear: function(){
This.top = 0;
}
};
The demo example is as follows:
var stack = new Stack();
stack.push("a");
stack.push("b");
stack.push("c");
console.log(stack.length()); // 3
console.log(stack.peek()); // c
var popped = stack.pop();
console.log(popped); // c
console.log(stack.peek()); // b
stack.push("d");
console.log(stack.peek()); // d
stack.clear();
console.log(stack.length()); // 0
console.log(stack.peek()); // undefined
Below we can implement a recursive definition of the factorial function; such as 5! The factorial of 5! = 5 * 4 * 3 * 2 * 1;
The following code:
function fact(n) {
var s = new Stack();
; while(n > 1) {
s.push(n--);
}
var product = 1;
While(s.length() > 0) {
Product *= s.pop();
}
Return product;
}
console.log(fact(5));
The meaning of the above code is: first pass the number 5 into the function, use a while loop, and push the function push() using the stack into the stack before decrementing it by 1 each time until the variable n is less than 1. Then define a variable product; use the length() method of the stack to determine whether it is greater than 0 and execute product* = s.pop() each time; the pop() method returns the top element of the stack and deletes the element from the stack. So each time it is executed, one element is deleted until s.length() <= 0. So product = 5*4*3*2*1 . and other operations.

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1376
1376
 52
52
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Compare complex data structures using Java function comparison
Apr 19, 2024 pm 10:24 PM
Compare complex data structures using Java function comparison
Apr 19, 2024 pm 10:24 PM
When using complex data structures in Java, Comparator is used to provide a flexible comparison mechanism. Specific steps include: defining the comparator class, rewriting the compare method to define the comparison logic. Create a comparator instance. Use the Collections.sort method, passing in the collection and comparator instances.
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
 Java data structures and algorithms: in-depth explanation
May 08, 2024 pm 10:12 PM
Java data structures and algorithms: in-depth explanation
May 08, 2024 pm 10:12 PM
Data structures and algorithms are the basis of Java development. This article deeply explores the key data structures (such as arrays, linked lists, trees, etc.) and algorithms (such as sorting, search, graph algorithms, etc.) in Java. These structures are illustrated through practical examples, including using arrays to store scores, linked lists to manage shopping lists, stacks to implement recursion, queues to synchronize threads, and trees and hash tables for fast search and authentication. Understanding these concepts allows you to write efficient and maintainable Java code.
 PHP data structure: The balance of AVL trees, maintaining an efficient and orderly data structure
Jun 03, 2024 am 09:58 AM
PHP data structure: The balance of AVL trees, maintaining an efficient and orderly data structure
Jun 03, 2024 am 09:58 AM
AVL tree is a balanced binary search tree that ensures fast and efficient data operations. To achieve balance, it performs left- and right-turn operations, adjusting subtrees that violate balance. AVL trees utilize height balancing to ensure that the height of the tree is always small relative to the number of nodes, thereby achieving logarithmic time complexity (O(logn)) search operations and maintaining the efficiency of the data structure even on large data sets.
 Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Groundbreaking CVM algorithm solves more than 40 years of counting problems! Computer scientist flips coin to figure out unique word for 'Hamlet'
Jun 07, 2024 pm 03:44 PM
Counting sounds simple, but in practice it is very difficult. Imagine you are transported to a pristine rainforest to conduct a wildlife census. Whenever you see an animal, take a photo. Digital cameras only record the total number of animals tracked, but you are interested in the number of unique animals, but there is no statistics. So what's the best way to access this unique animal population? At this point, you must be saying, start counting now and finally compare each new species from the photo to the list. However, this common counting method is sometimes not suitable for information amounts up to billions of entries. Computer scientists from the Indian Statistical Institute, UNL, and the National University of Singapore have proposed a new algorithm - CVM. It can approximate the calculation of different items in a long list.



