为什么0.1+0.2=0.30000000000000004而1.1+2.2=3.3000000000000003?
如图: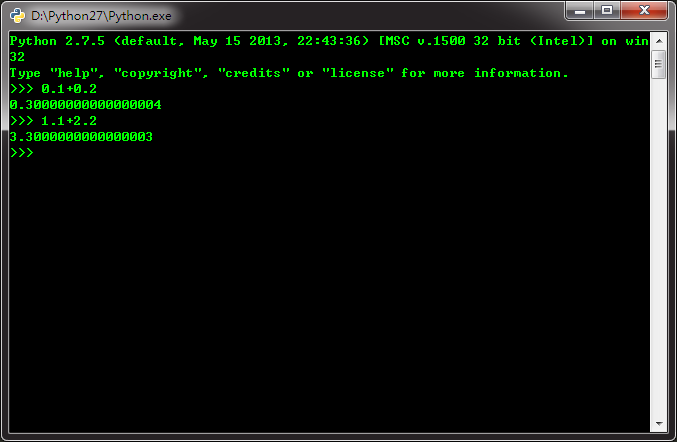
回复内容:
不管是什么数, 在计算机中最终都会被转化为 0 和 1 进行存储, 所以需要弄明白以下几点问题- 一个小数如何转化为二进制
- 浮点数的二进制如何存储
浮点数的二进制表示
首先我们要了解浮点数二进制表示, 有以下两个原则:
- 整数部分对 2 取余然后逆序排列
- 小数部分乘 2 取整数部分, 然后顺序排列
0.1 的表示是什么?
我们继续按照浮点数的二进制表示来计算
0.1 * 2 = 0.2 整数部分取 0
0.2 * 2 = 0.4 整数部分取 0
0.4 * 2 = 0.8 整数部分取 0
0.8 * 2 = 1.6 整数部分取 1
0.6 * 2 = 1.2 整数部分取 1
0.2 * 2 = 0.4 整数部分取 0
…
所以你会发现, 0.1 的二进制表示是 0.00011001100110011001100110011……0011
0011作为二进制小数的循环节不断的进行循环.
这就引出了一个问题, 你永远不能存下 0.1 的二进制, 即使你把全世界的硬盘都放在一起, 也存不下 0.1 的二进制小数.
浮点数的二进制存储
Python 和 C 一样, 采用 IEEE 754 规范来存储浮点数. IEEE 754 对双精度浮点数的存储规范将 64 bit 分为 3 部分.
- 第 1 bit 位用来存储 符号, 决定这个数是正数还是负数
- 然后使用 11 bit 来存储指数部分
- 剩下的 52 bit 用来存储尾数
Double-precision_floating-point_format
而且可以指出的是, double 能存储的数的个数是有限的, double 能代表的数必然不超过 2^64 个, 那么现实世界上有多少个小数呢? 无限个. 计算机能做的只能是一个接近这个小数的值, 是这个值在一定精度下与逻辑认为的值相等. 换句话说, 每个小数的存储(但是不是所有的), 都会伴有精度的丢失.
浮点数计算的问题
现在我们可以回顾你提出的问题
0.1 + 0.2 == 0.30.1 在计算机存储中真正的数字是 0.1000000000000000055511151231257827021181583404541015625
0.2 是
0.200000000000000011102230246251565404236316680908203125
0.3 是
0.299999999999999988897769753748434595763683319091796875
这就是为什么 0.1 + 0.2 != 0.3 的原因
至于 1.1 + 2.2 与之类似
首先声明这不是bug,原因在与十进制到二进制的转换导致的精度问题!其次这几乎出现在很多的编程语言中:C、C++、Java、Javascript、Python中,准确的说:“使用了IEEE754浮点数格式”来存储浮点类型(float 32,double 64)的任何编程语言都有这个问题!简要介绍下IEEE 754浮点格式:它用科学记数法以底数为2的小数来表示浮点数。IEEE浮点数(共32位)用1位表示数字符号,用8为表示指数,用23为来表示尾数(即小数部分)。此处指数用移码存储,尾数则是原码(没有符号位)。之所以用移码是因为移码的负数的符号位为0,这可以保证浮点数0的所有位都是0。双精度浮点数(64位),使用1位符号位、11位指数位、52位尾数位来表示。
因为科学记数法有很多种方式来表示给定的数字,所以要规范化浮点数,以便用底数为2并且小数点左边为1的小数来表示(注意是二进制的,所以只要不为0则一定有一位为1),按照需要调节指数就可以得到所需的数字。例如:十进制的1.25 => 二进制的1.01 => 则存储时指数为0、尾数为1.01、符号位为0.(十进制转二进制)
回到开头,为什么“0.1+0.2=0.30000000000000004”?首先声明这是javascript语言计算的结果(注意Javascript的数字类型是以64位的IEEE 754格式存储的)。正如同十进制无法精确表示1/3(0.33333...)一样,二进制也有无法精确表示的值。例如1/10。64位浮点数情况下:
十进制0.1=> 二进制0.00011001100110011...(循环0011)
=>尾数为1.1001100110011001100...1100(共52位,除了小数点左边的1),指数为-4(二进制移码为00000000010),符号位为0=> 存储为:0 00000000100 10011001100110011...11001=> 因为尾数最多52位,所以实际存储的值为0.00011001100110011001100110011001100110011001100110011001
十进制0.2=> 二进制0.0011001100110011...(循环0011)
=>尾数为1.1001100110011001100...1100(共52位,除了小数点左边的1),指数为-3(二进制移码为00000000011),符号位为0=> 存储为:0 00000000011 10011001100110011...11001
因为尾数最多52位,所以实际存储的值为0.00110011001100110011001100110011001100110011001100110011
两者相加:
0.00011001100110011001100110011001100110011001100110011001 + 0.00110011001100110011001100110011001100110011001100110011 = 0.01001100110011001100110011001100110011001100110011001100
转换成10进制之后得到:0.30000000000000004!
相关链接:
Language agnostic - Is floating point math broken? - Stack Overflow http://stackoverflow.com/questions/588004/is-floating-point-math-broken
Floating Point Arithmetic and Agent Based Models http://www.macaulay.ac.uk/fearlus/floating-point/ 因为二进制无法准确的描述十进制小数. 所以float的运算存在误差.
1.1+2.2跟0.1+0.2的计算结果不同是因为精度问题. 比如:
1.1= 1000000101E-9
0.1=101011....E-15
(上述数值通过手工计算可能存在问题)
具体题主可以看一下小数在计算机内存中的存储方式.

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 How Do I Use Beautiful Soup to Parse HTML?
Mar 10, 2025 pm 06:54 PM
How Do I Use Beautiful Soup to Parse HTML?
Mar 10, 2025 pm 06:54 PM
This article explains how to use Beautiful Soup, a Python library, to parse HTML. It details common methods like find(), find_all(), select(), and get_text() for data extraction, handling of diverse HTML structures and errors, and alternatives (Sel
 Mathematical Modules in Python: Statistics
Mar 09, 2025 am 11:40 AM
Mathematical Modules in Python: Statistics
Mar 09, 2025 am 11:40 AM
Python's statistics module provides powerful data statistical analysis capabilities to help us quickly understand the overall characteristics of data, such as biostatistics and business analysis. Instead of looking at data points one by one, just look at statistics such as mean or variance to discover trends and features in the original data that may be ignored, and compare large datasets more easily and effectively. This tutorial will explain how to calculate the mean and measure the degree of dispersion of the dataset. Unless otherwise stated, all functions in this module support the calculation of the mean() function instead of simply summing the average. Floating point numbers can also be used. import random import statistics from fracti
 Serialization and Deserialization of Python Objects: Part 1
Mar 08, 2025 am 09:39 AM
Serialization and Deserialization of Python Objects: Part 1
Mar 08, 2025 am 09:39 AM
Serialization and deserialization of Python objects are key aspects of any non-trivial program. If you save something to a Python file, you do object serialization and deserialization if you read the configuration file, or if you respond to an HTTP request. In a sense, serialization and deserialization are the most boring things in the world. Who cares about all these formats and protocols? You want to persist or stream some Python objects and retrieve them in full at a later time. This is a great way to see the world on a conceptual level. However, on a practical level, the serialization scheme, format or protocol you choose may determine the speed, security, freedom of maintenance status, and other aspects of the program
 How to Perform Deep Learning with TensorFlow or PyTorch?
Mar 10, 2025 pm 06:52 PM
How to Perform Deep Learning with TensorFlow or PyTorch?
Mar 10, 2025 pm 06:52 PM
This article compares TensorFlow and PyTorch for deep learning. It details the steps involved: data preparation, model building, training, evaluation, and deployment. Key differences between the frameworks, particularly regarding computational grap
 What are some popular Python libraries and their uses?
Mar 21, 2025 pm 06:46 PM
What are some popular Python libraries and their uses?
Mar 21, 2025 pm 06:46 PM
The article discusses popular Python libraries like NumPy, Pandas, Matplotlib, Scikit-learn, TensorFlow, Django, Flask, and Requests, detailing their uses in scientific computing, data analysis, visualization, machine learning, web development, and H
 How to Create Command-Line Interfaces (CLIs) with Python?
Mar 10, 2025 pm 06:48 PM
How to Create Command-Line Interfaces (CLIs) with Python?
Mar 10, 2025 pm 06:48 PM
This article guides Python developers on building command-line interfaces (CLIs). It details using libraries like typer, click, and argparse, emphasizing input/output handling, and promoting user-friendly design patterns for improved CLI usability.
 Scraping Webpages in Python With Beautiful Soup: Search and DOM Modification
Mar 08, 2025 am 10:36 AM
Scraping Webpages in Python With Beautiful Soup: Search and DOM Modification
Mar 08, 2025 am 10:36 AM
This tutorial builds upon the previous introduction to Beautiful Soup, focusing on DOM manipulation beyond simple tree navigation. We'll explore efficient search methods and techniques for modifying HTML structure. One common DOM search method is ex
 Explain the purpose of virtual environments in Python.
Mar 19, 2025 pm 02:27 PM
Explain the purpose of virtual environments in Python.
Mar 19, 2025 pm 02:27 PM
The article discusses the role of virtual environments in Python, focusing on managing project dependencies and avoiding conflicts. It details their creation, activation, and benefits in improving project management and reducing dependency issues.







