 Web Front-end
Web Front-end
 JS Tutorial
JS Tutorial
 Detailed explanation of binary tree of JavaScript data structures and algorithms_Basic knowledge
Detailed explanation of binary tree of JavaScript data structures and algorithms_Basic knowledge
Detailed explanation of binary tree of JavaScript data structures and algorithms_Basic knowledge
The concept of binary tree
Binary Tree is a finite set of n (n>=0) nodes. The set is either an empty set (empty binary tree), or it consists of a root node and two mutually disjoint trees. It is a binary tree consisting of the left subtree and the right subtree of the root node.

Characteristics of binary trees
Each node has at most two subtrees, so there is no node with degree greater than 2 in the binary tree. Each node in the binary tree is an object, and each data node has three pointers, which are pointers to the parent, left child, and right child. Each node is connected to each other through pointers. The relationship between connected pointers is a parent-child relationship.
Definition of binary tree node
Binary tree nodes are defined as follows:
struct BinaryTreeNode
{
int m_nValue;
BinaryTreeNode* m_pLeft;
BinaryTreeNode* m_pRight;
};
Five basic forms of binary trees
Empty binary tree
There is only one root node
The root node has only the left subtree
The root node has only the right subtree
The root node has both left and right subtrees

There are only two situations for an ordinary tree with three nodes: two layers or three layers. But since the binary tree needs to distinguish left and right, it will evolve into the following five forms:

Special Binary Tree
Slanted Tree
As shown in the 2nd and 3rd pictures in the last picture above.
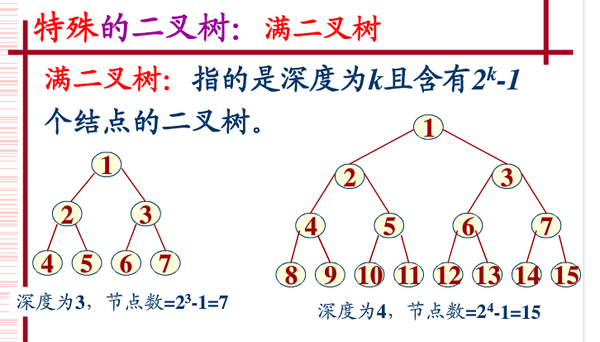
Full Binary Tree
In a binary tree, if all branch nodes have left subtrees and right subtrees, and all leaves are on the same level, such a binary tree is called a full binary tree. As shown below:
Complete Binary Tree
A complete binary tree means that the left side of the last level is full, the right side may be full or not, and then the remaining levels are full. A binary tree with depth k and number of nodes 2^k - 1 is a full binary tree (complete binary tree). It is a tree with depth k and no gaps.
The characteristics of a complete binary tree are:
Leaf nodes can only appear on the bottom two levels.
The lowest leaves must be concentrated on the left continuous position.
On the penultimate layer, if there are leaf nodes, they must be in continuous positions on the right.
If the node degree is 1, then the node has only left child.
A binary tree with the same node tree, a complete binary tree has the smallest depth.
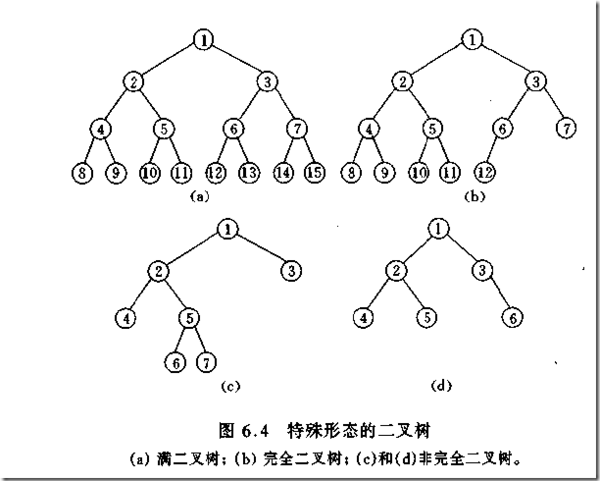
Note: A full binary tree must be a complete binary tree, but a complete binary tree is not necessarily a full binary tree.
The algorithm is as follows:
bool is_complete(tree *root)
{
queue q;
tree *ptr;
// Perform breadth-first traversal (level traversal) and put NULL nodes into the queue
q.push(root);
While ((ptr = q.pop()) != NULL)
{
q.push(ptr->left);
q.push(ptr->right);
}
// Determine whether there are any unvisited nodes
While (!q.is_empty())
{
ptr = q.pop();
// If there are unvisited non-NULL nodes, the tree has holes and is a non-complete binary tree
If (NULL != ptr)
return false;
}
return true;
}
Properties of binary trees
Property 1 of a binary tree: There are at most 2^(i-1) nodes (i>=1) on the i-th level of the binary tree
Property 2 of binary trees: A binary tree with depth k has at most 2^k-1 nodes (k>=1)
Sequential storage structure of binary tree
The sequential storage structure of a binary tree uses a one-dimensional array to store each node in the binary tree, and the storage location of the nodes can reflect the logical relationship between the nodes.

Binary linked list
Since the applicability of sequential storage is not strong, we must consider the chain storage structure. According to international practice, the storage of binary trees generally uses a chain storage structure.
Each node of a binary tree has at most two children, so it is a natural idea to design a data field and two pointer fields for it. We call such a linked list a binary linked list.

Binary tree traversal
Traversing a binary tree means starting from the root node and visiting all the nodes in the binary tree in a certain order so that each node is visited once and only once.
There are three ways to traverse a binary tree, as follows:
(1) Preorder traversal (DLR), first visit the root node, then traverse the left subtree, and finally traverse the right subtree. The abbreviation root-left-right.
(2) In-order traversal (LDR), first traverses the left subtree, then visits the root node, and finally traverses the right subtree. Abbreviated as left-root-right.
(3) Post-order traversal (LRD), first traverses the left subtree, then traverses the right subtree, and finally visits the root node. Abbreviated as left-right-root.
Preorder traversal:
If the binary tree is empty, no operation returns, otherwise the root node is visited first, then the left subtree is traversed in preorder, and then the right subtree is traversed in preorder.
The order of traversal is: A B D H I E J C F K G
//Pre-order traversal
function preOrder(node){
If(!node == null){
putstr(node.show() " ");
preOrder(node.left);
preOrder(node.right);
}
}
In-order traversal:
If the tree is empty, no operation returns, otherwise starting from the root node (note that the root node is not visited first), traverse the left subtree of the root node in in-order, then visit the root node, and finally Traverse the right subtree in order.

The order of traversal is: H D I B E J A F K C G
//Use recursion to implement in-order traversal
function inOrder(node){
If(!(node == null)){
inOrder(node.left);//Visit the left subtree first
putstr(node.show() " ");//Visit the root node again
inOrder(node.right);//Last access to the right subtree
}
}
Post-order traversal:
If the tree is empty, the no-op operation returns, otherwise the left and right subtrees are traversed from left to right, first the leaves and then the nodes, and finally the root node is visited.

The order of traversal is: H I D J E B K F G C A
//Post-order traversal
function postOrder(node){
If(!node == null){
PostOrder(node.left);
postOrder(node.right);
putStr(node.show() " ");
}
}
Implement binary search tree
Binary search tree (BST) is composed of nodes, so we define a Node node object as follows:
function Node(data,left,right){
This.data = data;
This.left = left;//Save the left node link
This.right = right;
This.show = show;
}
function show(){
Return this.data;//Display the data saved in the node
}
Find the maximum and minimum values
Finding the minimum and maximum values on a BST is very simple because the smaller value is always on the left child node. To find the minimum value on a BST, just traverse the left subtree until the last node is found
Find the minimum value
function getMin(){
var current = this.root;
While(!(current.left == null)){
Current = current.left;
}
Return current.data;
}
This method traverses the left subtree of the BST one by one until it traverses to the leftmost node of the BST, which is defined as:
current.left = null;
At this time, the value saved on the current node is the minimum value
Find the maximum value
Finding the maximum value on BST only requires traversing the right subtree until the last node is found, and the value saved on this node is the maximum value.
function getMax(){
var current = this.root;
While(!(current.right == null)){
current = current.right;
}
Return current.data;
}

Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 Chinese version
Chinese version, very easy to use

Zend Studio 13.0.1
Powerful PHP integrated development environment

Dreamweaver CS6
Visual web development tools

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Hot Topics
 1358
1358
 52
52
 1196
1196
 24
24
 Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Implementing Machine Learning Algorithms in C++: Common Challenges and Solutions
Jun 03, 2024 pm 01:25 PM
Common challenges faced by machine learning algorithms in C++ include memory management, multi-threading, performance optimization, and maintainability. Solutions include using smart pointers, modern threading libraries, SIMD instructions and third-party libraries, as well as following coding style guidelines and using automation tools. Practical cases show how to use the Eigen library to implement linear regression algorithms, effectively manage memory and use high-performance matrix operations.
 Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
Explore the underlying principles and algorithm selection of the C++sort function
Apr 02, 2024 pm 05:36 PM
The bottom layer of the C++sort function uses merge sort, its complexity is O(nlogn), and provides different sorting algorithm choices, including quick sort, heap sort and stable sort.
 Compare complex data structures using Java function comparison
Apr 19, 2024 pm 10:24 PM
Compare complex data structures using Java function comparison
Apr 19, 2024 pm 10:24 PM
When using complex data structures in Java, Comparator is used to provide a flexible comparison mechanism. Specific steps include: defining the comparator class, rewriting the compare method to define the comparison logic. Create a comparator instance. Use the Collections.sort method, passing in the collection and comparator instances.
 Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
Improved detection algorithm: for target detection in high-resolution optical remote sensing images
Jun 06, 2024 pm 12:33 PM
01 Outlook Summary Currently, it is difficult to achieve an appropriate balance between detection efficiency and detection results. We have developed an enhanced YOLOv5 algorithm for target detection in high-resolution optical remote sensing images, using multi-layer feature pyramids, multi-detection head strategies and hybrid attention modules to improve the effect of the target detection network in optical remote sensing images. According to the SIMD data set, the mAP of the new algorithm is 2.2% better than YOLOv5 and 8.48% better than YOLOX, achieving a better balance between detection results and speed. 02 Background & Motivation With the rapid development of remote sensing technology, high-resolution optical remote sensing images have been used to describe many objects on the earth’s surface, including aircraft, cars, buildings, etc. Object detection in the interpretation of remote sensing images
 Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
Application of algorithms in the construction of 58 portrait platform
May 09, 2024 am 09:01 AM
1. Background of the Construction of 58 Portraits Platform First of all, I would like to share with you the background of the construction of the 58 Portrait Platform. 1. The traditional thinking of the traditional profiling platform is no longer enough. Building a user profiling platform relies on data warehouse modeling capabilities to integrate data from multiple business lines to build accurate user portraits; it also requires data mining to understand user behavior, interests and needs, and provide algorithms. side capabilities; finally, it also needs to have data platform capabilities to efficiently store, query and share user profile data and provide profile services. The main difference between a self-built business profiling platform and a middle-office profiling platform is that the self-built profiling platform serves a single business line and can be customized on demand; the mid-office platform serves multiple business lines, has complex modeling, and provides more general capabilities. 2.58 User portraits of the background of Zhongtai portrait construction
 Java data structures and algorithms: in-depth explanation
May 08, 2024 pm 10:12 PM
Java data structures and algorithms: in-depth explanation
May 08, 2024 pm 10:12 PM
Data structures and algorithms are the basis of Java development. This article deeply explores the key data structures (such as arrays, linked lists, trees, etc.) and algorithms (such as sorting, search, graph algorithms, etc.) in Java. These structures are illustrated through practical examples, including using arrays to store scores, linked lists to manage shopping lists, stacks to implement recursion, queues to synchronize threads, and trees and hash tables for fast search and authentication. Understanding these concepts allows you to write efficient and maintainable Java code.
 PHP data structure: The balance of AVL trees, maintaining an efficient and orderly data structure
Jun 03, 2024 am 09:58 AM
PHP data structure: The balance of AVL trees, maintaining an efficient and orderly data structure
Jun 03, 2024 am 09:58 AM
AVL tree is a balanced binary search tree that ensures fast and efficient data operations. To achieve balance, it performs left- and right-turn operations, adjusting subtrees that violate balance. AVL trees utilize height balancing to ensure that the height of the tree is always small relative to the number of nodes, thereby achieving logarithmic time complexity (O(logn)) search operations and maintaining the efficiency of the data structure even on large data sets.
 News recommendation algorithm based on global graph enhancement
Apr 08, 2024 pm 09:16 PM
News recommendation algorithm based on global graph enhancement
Apr 08, 2024 pm 09:16 PM
Author | Reviewed by Wang Hao | Chonglou News App is an important way for people to obtain information sources in their daily lives. Around 2010, popular foreign news apps included Zite and Flipboard, while popular domestic news apps were mainly the four major portals. With the popularity of new era news recommendation products represented by Toutiao, news apps have entered a new era. As for technology companies, no matter which one they are, as long as they master the sophisticated news recommendation algorithm technology, they will basically have the initiative and voice at the technical level. Today, let’s take a look at a RecSys2023 Best Long Paper Nomination Award paper—GoingBeyondLocal:GlobalGraph-EnhancedP



