Algorithmes et exemples d'analyse de quatre expressions arithmétiques dans les compétences javascript_javascript

Lors de l'écriture de code, nous rencontrons parfois des situations où nous devons analyser nous-mêmes quatre expressions arithmétiques. Cet article présente brièvement l'utilisation de JavaScript pour analyser quatre expressions arithmétiques simples.

1. Concepts familiers

Notation infixe (ou notation infixe) est une méthode générale d'expression de formules arithmétiques ou logiques. L'opérateur est au milieu des opérandes sous forme infixe (exemple : 3 4). Autrement dit, nos expressions arithmétiques les plus couramment utilisées, les expressions infixes, sont plus faciles à comprendre pour les humains, mais pas faciles à analyser pour les ordinateurs.

La notation polonaise inversée (notation polonaise inversée, RPN ou notation polonaise inversée) est une méthode d'expression mathématique introduite par le mathématicien polonais Jan Vukasiewicz en 1920. Dans la notation polonaise inversée, tous les opérateurs sont placés après les opérandes. , c'est pourquoi on l'appelle aussi notation de suffixe. La notation polonaise inversée ne nécessite pas de parenthèses pour indiquer la priorité des opérateurs. La notation polonaise inversée facilite l'utilisation d'une structure de pile pour analyser et calculer des expressions. Par conséquent, nous analysons ici les expressions à quatre éléments en convertissant d'abord l'expression infixe en une expression polonaise inversée. Calculez ensuite la valeur.

2. Processus de conversion

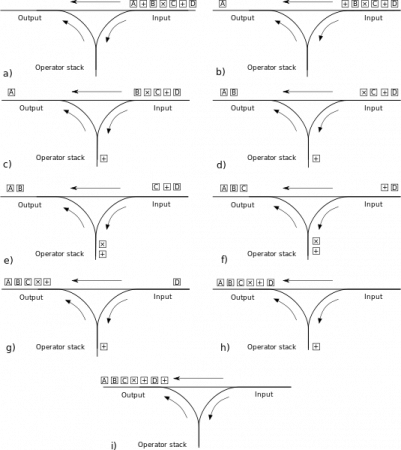
Convertir l'expression infixe en expression postfixe (algorithme de champ de planification)

1. Une marque apparaît dans la file d'attente de saisie
2. Si le jeton est un nombre, ajoutez-le à la file d'attente de sortie
3. S'il s'agit d'un opérateur (-*/), comparez-le avec l'opérateur en haut de la pile de sortie. Si la priorité est inférieure ou égale à l'opérateur en haut de la pile, placez l'opérateur en haut. de la pile et ajoutez-le à la file d'attente de sortie (boucle jusqu'à ce que les conditions ci-dessus ne soient pas remplies), et enfin poussez cet opérateur sur la pile.
4. S'il s'agit d'une parenthèse gauche, poussez-la sur la pile
5. S'il s'agit d'une parenthèse droite, extrayez continuellement les opérateurs de la pile et ajoutez-les à la file d'attente de sortie jusqu'à ce que l'élément en haut de la pile soit la parenthèse gauche. Pop le crochet gauche et ne l'ajoute pas à la file d'attente de sortie. Si le crochet gauche n'est pas trouvé, cela signifie que les crochets dans l'expression originale ne sont pas symétriques et qu'il y a une erreur.
6. Si la file d'attente d'entrée est vide et qu'il y a encore des opérateurs sur la pile, si l'opérateur en haut de la pile est une parenthèse gauche, cela signifie que l'expression d'origine a des parenthèses sans correspondance. Extrayez les opérateurs de la pile un par un et ajoutez-les à la file d'attente de sortie.
7. Terminez

3. Implémentation de la conversion de code

function isOperator(value){
	var operatorString = "+-*/()";
	return operatorString.indexOf(value) > -1
}

function getPrioraty(value){
	switch(value){
		case '+':
		case '-':
			return 1;
		case '*':
		case '/':
			return 2;
		default:
			return 0;
	}
}

function prioraty(o1, o2){
	return getPrioraty(o1) <= getPrioraty(o2);
}

function dal2Rpn(exp){
	var inputStack = [];
	var outputStack = [];
	var outputQueue = [];

	for(var i = 0, len = exp.length; i < len; i++){
		var cur = exp[i];
		if(cur != ' ' ){
			inputStack.push(cur);
		}
	}
	console.log('step one');
	while(inputStack.length > 0){
		var cur = inputStack.shift();
		if(isOperator(cur)){
			if(cur == '('){
				outputStack.push(cur);
			}else if(cur == ')'){
				var po = outputStack.pop();
				while(po != '(' && outputStack.length > 0){
					outputQueue.push(po);
					po = outputStack.pop();
				}
				if(po != '('){
					throw "error: unmatched ()";
				}
			}else{
				while(prioraty(cur, outputStack[outputStack.length - 1]) && outputStack.length > 0){
					outputQueue.push(outputStack.pop());
				}
				outputStack.push(cur);
			}
		}else{
			outputQueue.push(new Number(cur));
		}
	}
	console.log('step two');
	if(outputStack.length > 0){
		if(outputStack[outputStack.length - 1] == ')' || outputStack[outputStack.length - 1] == '('){
			throw "error: unmatched ()";
		}
		while(outputStack.length > 0){
			outputQueue.push(outputStack.pop());
		}
	}
	console.log('step three');
	return outputQueue;

}

console.log(dal2Rpn('1 + 2'));
console.log(dal2Rpn('1 + 2 + 3'));
console.log(dal2Rpn('1 + 2 * 3'));
console.log(dal2Rpn('1 + 2 * 3 - 4 / 5'));
console.log(dal2Rpn('( 1 + 2 )'));

console.log(dal2Rpn('( 1 + 2 ) * ( 3 - 4 ) / 5'));
console.log(dal2Rpn('( 1 + 2 ) * (( 3 - 4 ) / 5)'));

4. Évaluation de l'expression polonaise inversée

1. Extrayez un jeton de la file d'attente d'entrée
2. S'il s'agit d'un opérande, ajoutez-le à la pile de sortie
3. S'il s'agit d'un opérateur, extrayez les deux opérandes de la pile de sortie et effectuez des calculs, puis transférez la valeur calculée sur la pile de sortie.
4. Opération en boucle, si la file d'attente d'entrée est vide et que la pile de sortie n'a qu'un seul numéro, ce numéro est le résultat, sinon il y a des opérandes redondants.

5.Code de calcul

function evalRpn(rpnQueue){
	var outputStack = [];
	while(rpnQueue.length > 0){
		var cur = rpnQueue.shift();

		if(!isOperator(cur)){
			outputStack.push(cur);
		}else{
			if(outputStack.length < 2){
				throw "unvalid stack length";
			}
			var sec = outputStack.pop();
			var fir = outputStack.pop();

			outputStack.push(getResult(fir, sec, cur));
		}
	}

	if(outputStack.length != 1){
		throw "unvalid expression";
	}else{
		return outputStack[0];
	}
}

6.Conclusion

La notation polonaise inversée n'est pas quelque chose à laquelle vous êtes habitué lorsque vous entrez en contact avec elle, mais après vous être familiarisé avec elle, vous constaterez que l'idée est en fait très simple, contrairement à la notation infixe, qui a diverses priorités et parenthèses. Classe, la logique est particulièrement gênante, mais la notation polonaise inversée est plus concise, il n'est pas du tout nécessaire de considérer la priorité, et il n'est pas nécessaire d'utiliser des parenthèses, des crochets et des accolades pour perturber la situation.