 Tutoriel logiciel
Tutoriel logiciel
 Logiciel
Logiciel
 Méthode détaillée pour trouver les racines d'une équation quadratique à l'aide de Geometry Sketchpad
Méthode détaillée pour trouver les racines d'une équation quadratique à l'aide de Geometry Sketchpad
Méthode détaillée pour trouver les racines d'une équation quadratique à l'aide de Geometry Sketchpad
Geometry Sketchpad Trouvez les racines des équations quadratiques La résolution d'équations quadratiques est un problème courant en mathématiques. Geometry Sketchpad, un logiciel de dessin géométrique, constitue un moyen efficace de résoudre de telles équations. Dans cet article, l'éditeur PHP Baicao présentera en détail le processus complet d'utilisation du carnet de croquis géométrique pour trouver les racines d'une équation quadratique d'une variable. Cet article montrera étape par étape comment construire le graphique d'une équation, exploiter les propriétés géométriques et dériver les valeurs exactes des racines. Il est conseillé aux lecteurs de lire attentivement les détails suivants pour maîtriser les étapes et techniques spécifiques de cette méthode.
Étape 1 : Ouvrez le logiciel et définissez trois paramètres. Cliquez sur [Données] dans le menu supérieur et sélectionnez [Nouveau paramètre] dans le menu déroulant contextuel. Dans la petite fenêtre qui apparaît, remplacez t1 par a, sélectionnez sans unité et définissez la valeur par défaut, puis cliquez sur OK. De la même manière, établissez les deux autres paramètres b et le paramètre c. Laissez leurs valeurs être d'abord 1, puis vous pourrez modifier les valeurs des paramètres à volonté.
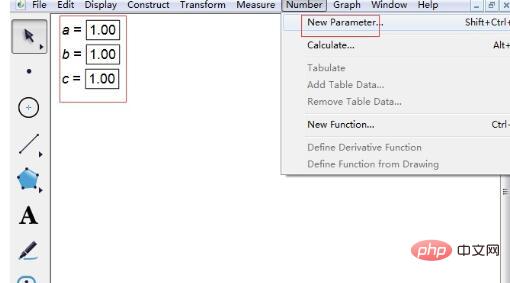
Étape 2 Entrez l'expression de la fonction de l'équation quadratique. Cliquez sur [Dessiner] dans le menu supérieur, sélectionnez l'option de nouvelle fonction Dessiner et saisissez l'expression dans la boîte de dialogue contextuelle. Il y a quelques points à noter lors de la saisie d'expressions. 1. Lors de la saisie du paramètre a, cliquez sur le paramètre a dans le coin supérieur gauche pour saisir. Cliquez ensuite sur le signe de multiplication * pour saisir x. Il en va de même pour les autres paramètres.
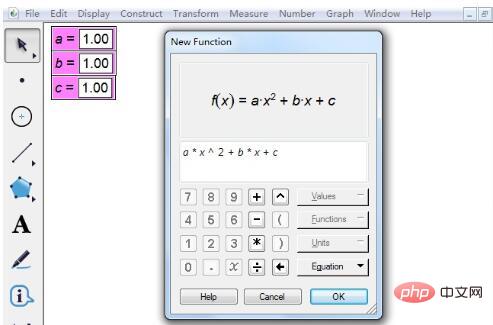
Étape 3 Modifiez les valeurs des paramètres. Après avoir saisi l'expression, cliquez sur [OK] pour dessiner un graphique comme indiqué ci-dessous. Évidemment, il n'a pas d'intersection avec l'axe horizontal et l'équation quadratique correspondante n'a pas de véritables racines. Donc, pour modifier la valeur du paramètre, double-cliquez sur le paramètre a et une petite fenêtre apparaîtra. Entrez simplement la valeur spécifique. Il en va de même pour les autres paramètres.
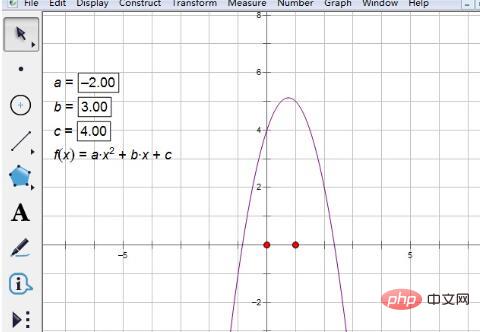
Étape 4 Sélectionnez l'outil de fonction. Cliquez sur le bouton [Outil personnalisé] dans la barre d'outils de gauche et sélectionnez [Outil de fonction] dans l'option de raccourci contextuel - la racine de f(x)=0.
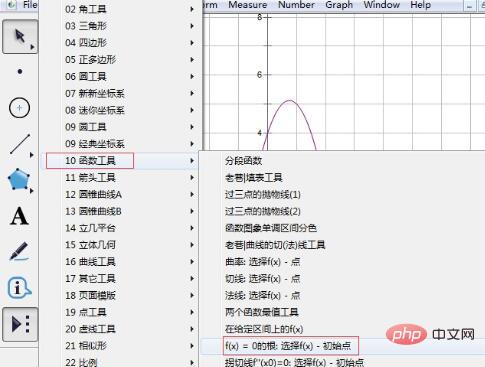
Étape 5 Trouvez les racines de l'équation. Cliquez une fois sur l'expression d'analyse de fonction, déplacez le curseur, l'étiquette racine apparaît et une racine s'affiche. Cliquez à nouveau sur l'expression, déplacez le curseur, une autre étiquette racine apparaît et la deuxième racine s'affiche.
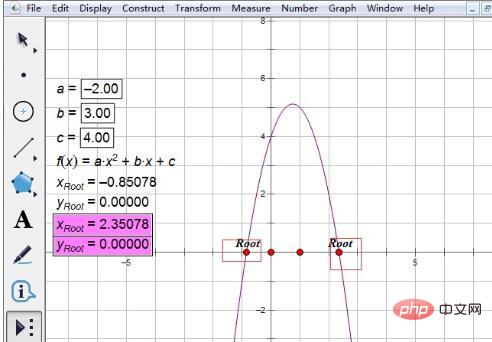
Conseils : De cette façon, les deux racines réelles de l'équation quadratique ont été trouvées. Notez que les deux valeurs x sont les racines et y est l'ordonnée. Alors comment trouver les racines d’une équation quadratique à coefficients arbitraires ? La méthode est très simple. Il vous suffit de double-cliquer sur les paramètres, de modifier les valeurs de a, b et c, et les racines de la nouvelle équation s'afficheront immédiatement.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1662
1662
 14
14
 1419
1419
 52
52
 1311
1311
 25
25
 1261
1261
 29
29
 1234
1234
 24
24
 Combien coûte Microsoft PowerToys?
Apr 09, 2025 am 12:03 AM
Combien coûte Microsoft PowerToys?
Apr 09, 2025 am 12:03 AM
Microsoft PowerToys est gratuit. Cette collection d'outils développée par Microsoft est conçue pour améliorer les fonctions du système Windows et améliorer la productivité des utilisateurs. En installant et en utilisant des fonctionnalités telles que FancyZones, les utilisateurs peuvent personnaliser les dispositions de fenêtres et optimiser les workflows.
 Quelle est la meilleure alternative à PowerToys?
Apr 08, 2025 am 12:17 AM
Quelle est la meilleure alternative à PowerToys?
Apr 08, 2025 am 12:17 AM
TheBestalternatiVestOpowerToySforwindowSersaReAutoHotkey, Windowgrid, andwinaerotweaker.1) AutoHotKeyOffersExtensivesScriptingForAutomation.2) WindowgridProvidesInSitiveGrid-basez-basywindowmanagement.3)
 Microsoft PowerToys a-t-il besoin d'une licence?
Apr 07, 2025 am 12:04 AM
Microsoft PowerToys a-t-il besoin d'une licence?
Apr 07, 2025 am 12:04 AM
Microsoft PowerToys ne nécessite pas de licence et est un logiciel open source gratuit. 1.PowerToys fournit une variété d'outils, tels que FancyEzones pour la gestion des fenêtres, PowerRename pour le changement de nom et ColorPicker pour la sélection des couleurs. 2. Les utilisateurs peuvent activer ou désactiver ces outils en fonction de leurs besoins pour améliorer l'efficacité du travail.



