 Périphériques technologiques
Périphériques technologiques
 IA
IA
 Aperçu de la planification du chemin : basé sur l'échantillonnage, la recherche et l'optimisation, tout est fait !
Aperçu de la planification du chemin : basé sur l'échantillonnage, la recherche et l'optimisation, tout est fait !
Aperçu de la planification du chemin : basé sur l'échantillonnage, la recherche et l'optimisation, tout est fait !
1 Aperçu du contrôle décisionnel et de la planification des mouvements
Les méthodes actuelles de contrôle décisionnel peuvent être divisées en trois catégories : la planification séquentielle, la planification sensible au comportement et la planification de bout en bout.
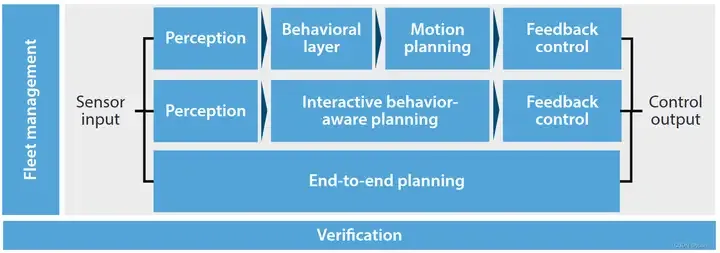
- planification séquentielle : La méthode la plus traditionnelle, les trois parties de perception, décision et contrôle sont relativement claires
- planification consciente du comportement : par rapport à la première méthode, le point culminant est la ; introduction de la collaboration homme-machine Conduite, collaboration véhicule-route et estimation des risques des véhicules pour l'environnement dynamique externe
- planification de bout en bout : la technologie DL et DRL, à l'aide d'une grande quantité de données de formation, obtient informations allant des informations sensorielles telles que les images aux entrées de commande du véhicule telles que les angles du volant. La relation est l'une des méthodes les plus populaires de nos jours.
Cet article présentera la planification séquentielle, décrira le processus de contrôle de perception des véhicules autonomes selon l'ensemble de la séquence de contrôle décisionnel, et enfin résumera brièvement les problèmes à résoudre mentionnés ci-dessus. "Architecture de contrôle pour les véhicules automatisés" décrite dans cet article La planification appartient aux première et troisième étapes.
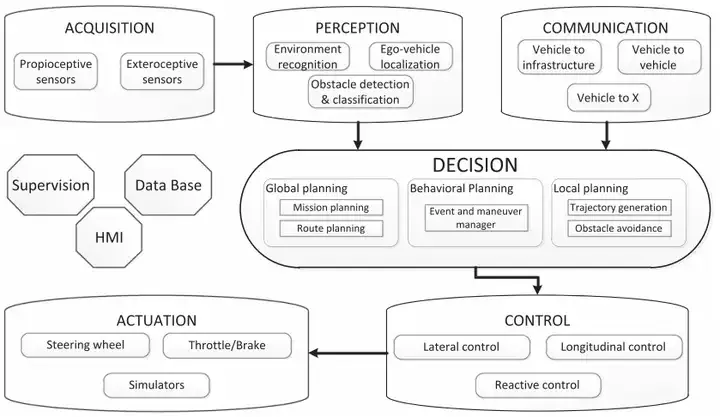
Concernant le problème de génération de trajectoire pour les véhicules sans pilote, il existe deux types :
méthode de génération de trajectoire directeet path-veloc méthode de décomposition de l'entité , par rapport au premier type, la vitesse de déplacement est moins difficile, elle est donc plus couramment utilisée. 2.1 Types de planification de chemin
La planification de chemin peut être divisée en quatre grandes catégories : les algorithmes basés sur le 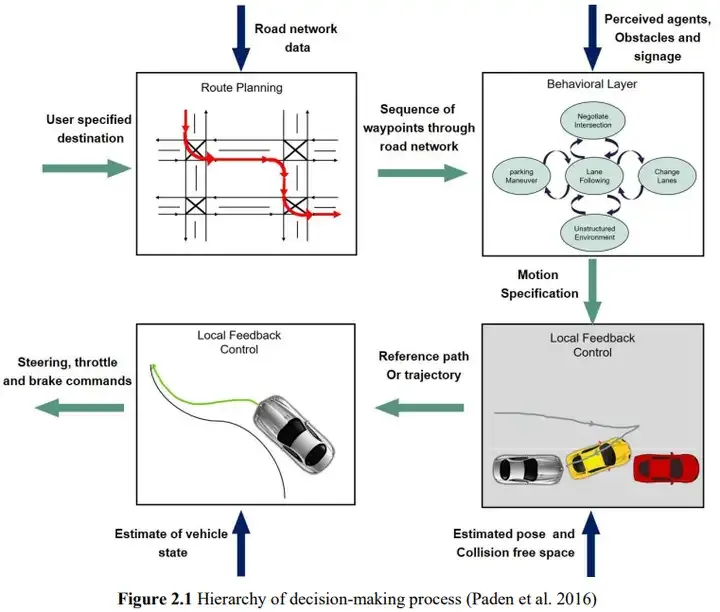 sampling
sampling
recherche représentée par A* et D*, La génération de trajectoire algorithme basé sur interpolation
ajustement représenté par la courbe β-spline, et l'algorithme de contrôleoptimal pour la planification de chemin local représenté par MPC. Cette section sera expliquée dans l'ordre ci-dessus :
A Review of Motion Planning Technology Algorithm
3.1.1 Algorithme de base PRM et RRT(1) PRM
Algorithme PRM (Feuille de route probabiliste). Le PRM se compose principalement de deux étapes, l’une est l’étape d’apprentissage et l’autre est l’étape de requête. 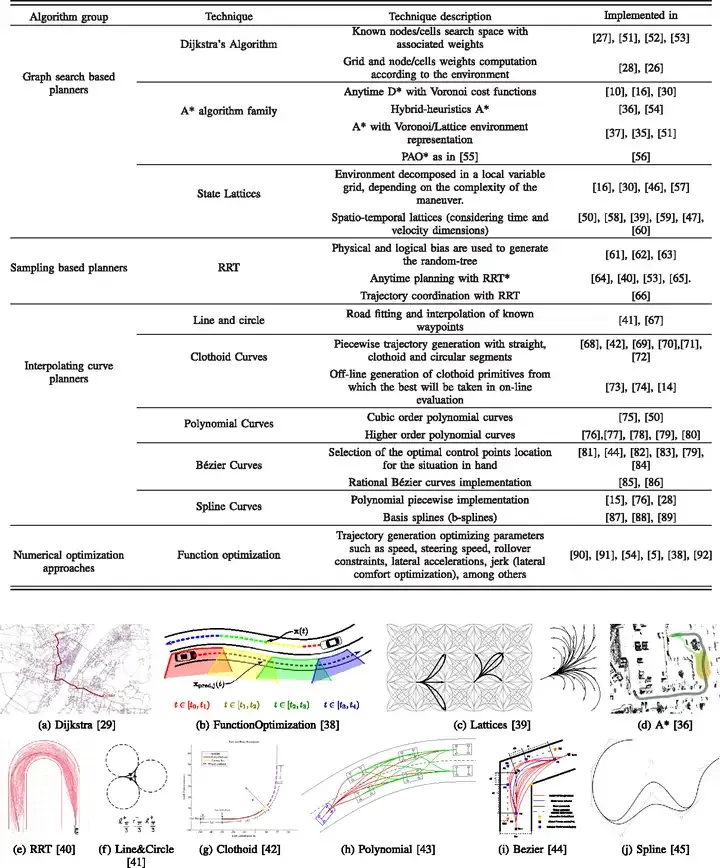
Une fois la construction du PRM terminée, il peut être utilisé pour résoudre des problèmes de planification de mouvement dans différents états initiaux et cibles, mais cette fonctionnalité n'est pas nécessaire pour la planification de mouvement de véhicules sans pilote. De plus, le PRM nécessite des connexions précises entre les états, ce qui est très difficile pour les problèmes de planification de mouvement avec des contraintes différentielles complexes.
(2) Algorithme RRT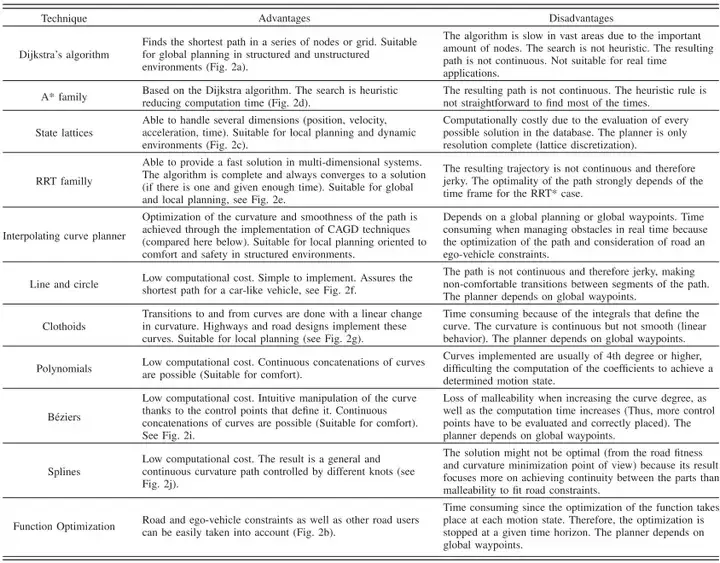
RRT (Arbre aléatoire à exploration rapide). RRT représente en fait une série d'algorithmes basés sur l'idée de arbres à croissance aléatoire. C'est actuellement l'algorithme le plus utilisé avec le plus de variantes d'optimisation dans le domaine de la robotique
① Initialisation de l'arbre. ensemble de nœuds et ensemble de bords de l'arbre, l'ensemble de nœuds ne contient que l'état initial et l'ensemble de bords est vide
;
② Croissance de l'arbre : échantillonnez aléatoirement l'espace d'états. Lorsque le point d'échantillonnage se trouve dans la zone de sécurité de l'espace d'états, sélectionnez le nœud le plus proche du point d'échantillonnage dans l'arbre actuel et étendez-le jusqu'au point d'échantillonnage généré ; la trajectoire n'est pas connectée à l'obstacle Si un objet entre en collision, la trajectoire est ajoutée à l'ensemble de bords de l'arbre et le point final de la trajectoire est ajouté à l'ensemble de nœuds de l'arbre
③ Répétez l'étape ② jusqu'à ce qu'elle soit développée à l'ensemble d'états cibles. Par rapport au graphe non orienté de PRM, RRT Ce qui est construit est une structure arborescente avec l'état initial comme nœud racine et l'état cible comme nœud feuille. Pour différents états initial et cible, différents arbres doivent être construits. être construit.
RRT ne nécessite pas de connexions précises entre les états et est plus adapté à la résolution de problèmes de dynamique de mouvement tels que la planification de mouvements de véhicules sans pilote.
3.1.2 Problèmes et solutions de la méthode d'échantillonnage
Résoudre l'efficacité et savoir si c'est la solution optimale. La raison pour laquelle PRM et RRT ont une exhaustivité probabiliste est qu'ils traverseront presque toutes les positions dans l'espace de configuration.
(1) Efficacité de résolution
En termes d'amélioration de efficacité de résolution, l'idée centrale de l'optimisation du RRT est de guider l'arbre vers la zone ouverte, c'est-à-dire d'essayer de rester à l'écart obstacles et éviter les contrôles répétés des nœuds au niveau des obstacles. Cela améliore l'efficacité. La solution principale :
① Échantillonnage uniforme
L'algorithme RRT standard échantillonne l'espace d'état de manière uniforme et aléatoire. La probabilité qu'un nœud dans l'arbre actuel obtienne une expansion est proportionnelle à sa zone de région de Voronoi, donc l'arbre se déplacera vers l'état. Les régions vides de l'espace grandissent, remplissant uniformément les régions libres de l'espace d'état. L'algorithme
RRT-connect construit simultanément deux arbres à partir de état initialet cibleétat respectivement Lorsque les deux arbres grandissent ensemble, une solution réalisable est trouvée. Go-biaing insère l'état cible dans une certaine proportion dans la séquence d'échantillonnage aléatoire, guidant l'arbre pour qu'il se développe vers l'état cible, accélérant la solution et améliorant la qualité de la solution.
heuristic RRT utilise une fonction heuristique pour augmenter la probabilité d'échantillonner des nœuds avec de faibles coûts d'expansion et calculer le coût de chaque nœud de l'arborescence. Cependant, dans des environnements complexes, la définition de la fonction de coût est difficile à résoudre. f La méthode d'échantillonnage biaisé discrétise d'abord l'espace d'état dans une grille, puis utilise l'algorithme de Dijkstra pour calculer le coût sur chaque grille. La valeur du coût des points dans la zone de la grille est égale à cette valeur. , construisant ainsi une fonction heuristique.
② Métrique de distance optimisée
La distance est utilisée pour mesurer le coût du chemin entre deux configurations, aide à générer une fonction de coût heuristique et guide la direction de l'arbre. Cependant, le calcul de la distance est difficile lorsque les obstacles sont pris en compte. La définition de la distance dans la planification de mouvement adopte une définition similaire à la distance euclidienne. RG-RRT (RRT guidé par rechabilité) peut éliminer l'impact d'une distance inexacte sur la capacité d'exploration RRT. Il doit calculer l'ensemble de nœuds accessible dans l'arborescence lorsque la distance entre le point d'échantillonnage et le nœud est supérieure à l'ensemble de nœuds accessible. le nœud, la distance, le nœud peut être sélectionné pour l'expansion.
③ Réduire le nombre de contrôles de collision
L'un des goulots d'étranglement d'efficacité de la méthode d'échantillonnage des contrôles de collision est que l'approche habituelle consiste à discrétiser le chemin à distances égales, puis à effectuer des contrôles de collision sur la configuration à chaque indiquer. résolution complète RRT obtient la probabilité d'expansion en réduisant les nœuds proches des obstacles Il discrétise l'espace d'entrée et ne l'utilise qu'une seule fois pour une certaine entrée de nœud si la trajectoire correspondant à une certaine entrée entre en collision avec un obstacle, alors le A correspondant ; Une valeur de pénalité est ajoutée au nœud. Plus la valeur de pénalité est élevée, plus la probabilité que le nœud soit étendu est faible. Le domaine dynamique RRT et le domaine dynamique adaptatif RRT limitent la zone d'échantillonnage à l'espace local où se trouve l'arborescence actuelle pour empêcher les nœuds proches des obstacles d'échecs d'expansion répétés et améliorer l'efficacité de l'algorithme.
④ Améliorer les performances en temps réel
À tout moment, RRT crée d'abord rapidement un RRT, obtient une solution réalisable et enregistre son coût, puis continue l'échantillonnage, mais insère uniquement les nœuds bénéfiques pour réduire le coût de la solution réalisable dans l'arbre, obtenant ainsi progressivement une meilleure solution réalisable. La replanification décompose l'ensemble de la tâche de planification en un certain nombre de séquences de sous-tâches de même durée et planifie la tâche suivante tout en exécutant la tâche en cours.
(2) Il existe principalement les méthodes suivantes pour résoudre le problème de l'optimalité :
Algorithme RGG (graphe géométrique aléatoire) : un PRM avec des propriétés asymptotiques optimales qui est amélioré par rapport au PRM et RRT standard basé sur la théorie des graphes géométriques aléatoires Les algorithmes RRG et RRT échantillonnent aléatoirement n points dans l'espace d'état et connectent les points dont la distance est inférieure à r(n) pour former RGG.
Algorithme RRT* : introduisez l'étape de "reconnexion" basée sur RRG pour vérifier si le nœud nouvellement inséré en tant que nœud parent de son point adjacent réduira le coût de son point adjacent. Si c'est le cas, supprimez le parent et l'enfant d'origine de. le point adjacent. Relation, prenant le point d'insertion actuel comme nœud parent, c'est l'algorithme RRT*.
Algorithme LBT-RRT : Un grand nombre de connexions de nœuds et d'ajustements locaux rendent PRM et RRT très inefficaces. L'algorithme LBT-RRT combine les algorithmes RRG et RRT* pour obtenir une efficacité plus élevée sur la base de l'obtention d'une optimalité asymptotique.
3.2 Algorithme basé sur la recherche
L'idée de base est de discrétiser l'espace d'état dans un graphe d'une certaine manière, puis d'utiliser divers algorithmes de recherche heuristiques pour rechercher des solutions réalisablesou même solutions optimales , cet algorithme de catégorie est relativement mature.
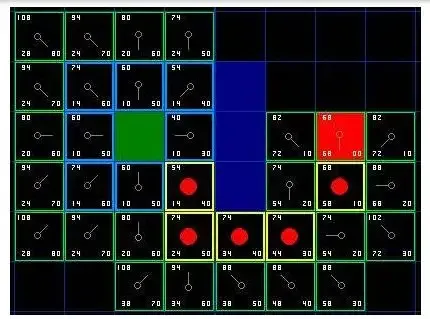
La base de l'algorithme basé sur la recherche est le réseau d'états. Le réseau d'états est une discrétisation de l'espace d'états et une primitive de mouvement qui part du nœud et atteint le nœud adjacent. Un nœud d'état peut transmettre ses transformations primitives de mouvement à un autre nœud d'état. Le réseau d'états convertit l'espace d'états continu d'origine en un graphe de recherche. Le problème de planification de mouvement consiste à rechercher une série de primitives de mouvement qui transforment l'état initial en état cible dans le graphe. Après avoir construit le réseau d'états, vous pouvez utiliser la recherche graphique. algorithme pour rechercher la trajectoire optimale.
3.2.1 Construction des algorithmes de base Dijkstra et A*
L'algorithme de Dijkstra parcourt tout l'espace de configuration, trouve la distance entre chacune des deux grilles et sélectionne enfin le chemin le plus court du point de départ au point cible, avec la largeur La nature prioritaire conduit à une très faible efficacité. L'ajout d'une fonction heuristique à cet algorithme, c'est-à-dire la distance entre le nœud recherché et le nœud cible, et une nouvelle recherche basée sur cela peut éviter l'inefficacité causée par la recherche globale. , comme le montre la figure ci-dessous, le rouge est la zone de recherche.
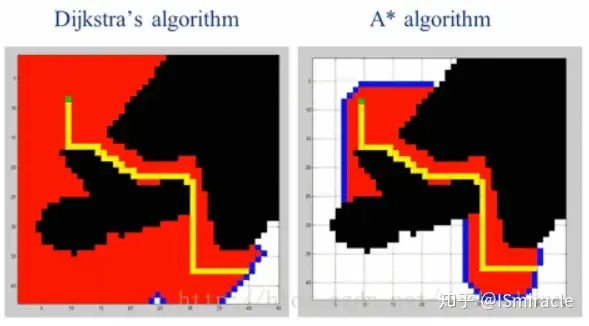
Figure 6 : Comparaison des effets des algorithmes A* et Dijkstra
3.2.2 Problèmes et suggestions de méthodes de recherche
Tout comme les algorithmes basés sur l'échantillonnage, ce type d'algorithme doit également être efficace et optimisation sexuelle optimale.
En termes d'amélioration de l'efficacité, A* lui-même est un algorithme de planification statique. Une extension de l'algorithme A* est pondérée A*, qui guide davantage la direction de recherche vers le nœud cible en augmentant le poids de la fonction heuristique. la vitesse est très rapide, mais il est facile de tomber dans les minima locaux et ne peut garantir la solution globale optimale.
Pour les véhicules en mouvement, l’utilisation de l’algorithme dérivé D de A* (A dynamique) peut grandement améliorer l’efficacité. LPA est également basé sur la programmation dynamique. Cet algorithme peut gérer la situation dans laquelle le coût des primitives de mouvement de la grille d'état varie dans le temps. Lorsque l'environnement change, un nouveau plan optimal peut être planifié en recherchant un plus petit nombre de. nœuds. Développé sur la base du LPA, D*-Lite peut atteindre les mêmes résultats que D*, mais avec une efficacité supérieure.
Lors de la recherche de solutions optimales, ARA* est un algorithme de recherche à tout moment développé sur la base de Weighted A*. Il appelle l'algorithme Weighted A* plusieurs fois et réduit le poids de la fonction heuristique à chaque appel, de sorte que l'algorithme. peut rapidement trouver une solution réalisable. En introduisant l'ensemble INCONS, chaque cycle peut continuer à utiliser les informations du cycle précédent pour optimiser le chemin et s'approcher progressivement de la solution optimale.
En termes d'équilibrage de l'efficacité et de l'optimalité de l'algorithme, Sandin Aine et al. ont proposé l'algorithme MHA*, qui a introduit plusieurs fonctions heuristiques pour garantir que l'une des fonctions heuristiques peut trouver la solution optimale lorsqu'elle est utilisée seule, donc par coordination. générés par différentes fonctions heuristiques peuvent prendre en compte l’efficacité et l’optimalité de l’algorithme. DMHA génère des fonctions heuristiques appropriées en ligne et en temps réel sur la base de MHA, évitant ainsi le problème du minimum local.
3.3 Algorithme basé sur l'ajustement par interpolation
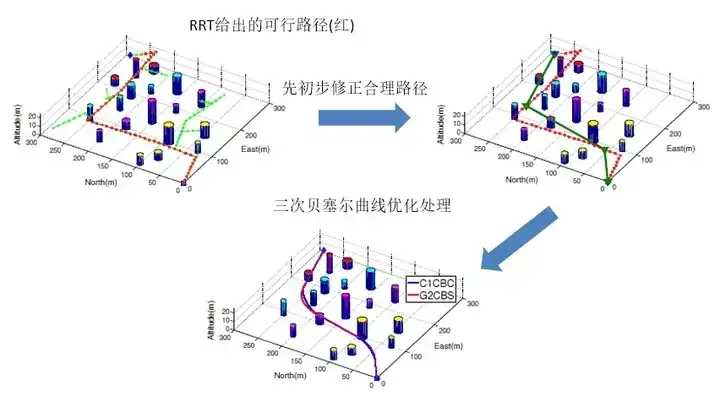
L'algorithme basé sur l'ajustement par interpolation peut être défini comme : basé sur une série connue d'ensembles de points utilisés pour décrire la feuille de route, en utilisant l'interpolation de données et Le La méthode d'ajustement de courbe crée le chemin sur lequel la voiture intelligente se déplacera, ce qui peut offrir une meilleurecontinuité et unedifférentiabilité plus élevée. La méthode spécifique est la suivante :
La courbe de Dubins et la courbe de Reeds et Sheep (RS) sont les chemins les plus courts reliant deux points quelconques de l'espace de configuration, correspondant respectivement aux situations sans inversion et avec inversion. Ils sont tous composés d'arcs et de lignes droites avec une courbure maximale. Il existe une discontinuité de courbure au niveau de la connexion entre l'arc et la ligne droite. Lorsqu'un véhicule réel suit une telle courbe, il doit s'arrêter et ajuster le volant au niveau de la discontinuité. de courbure pour continuer à rouler.La courbe d'interpolation polynomiale est la méthode la plus couramment utilisée. Elle peut définir des coefficients polynomiaux en répondant aux exigences des nœuds et obtenir une meilleure différentiabilité continue. Les polynômes du quatrième ordre sont souvent utilisés pour le contrôle des contraintes longitudinales, et les polynômes du cinquième ordre le sont souvent. utilisé pour le contrôle des contraintes longitudinales. Les polynômes sont souvent utilisés dans le contrôle des contraintes latérales, et les polynômes du troisième ordre sont également utilisés pour dépasser les trajectoires.
Courbe spline a une expression fermée et peut facilement assurer la continuité de la courbure. Les courbes β-spline peuvent assurer la continuité de la courbure, et les courbes de Bézier cubiques peuvent assurer la continuité et les limites de la courbure, et la quantité de calcul est relativement faible. La courbe η^3 [43] est une courbe spline du septième ordre, qui possède de très bonnes propriétés : continuité de courbure et continuité des dérivées de courbure, ce qui est très significatif pour les véhicules à grande vitesse.
3.4 Algorithmes basés sur un contrôle optimal
Les algorithmes basés sur un contrôle optimal sont classés dans la planification de trajectoire, principalement parce que MPC peut effectuer une planification de trajectoire locale pour éviter les obstacles. De plus, MPC a principalement pour fonction de suivre la trajectoire. aux contraintes dynamiques et cinématiques nécessaires, les questions qu'il considère doivent également prendre en compte le confort, l'incertitude des informations sensorielles, l'incertitude de la communication inter-véhicules à l'avenir et lors de la planification d'une trajectoire locale, le conducteur peut également être inclus dans la boucle de contrôle. Les problèmes d'incertitude mentionnés ci-dessus et l'intégration du pilote dans la boucle de contrôle seront abordés dans la section 4. L'étude du MPC commence principalement par deux aspects : la théorie de l'optimisation et la pratique de l'ingénierie. Pour le premier, je recommande Convex Optimization Algorithms de Dimitri P. Bertsekas et Model Predictive Control: Theory, Computation, and Design de James B. Rawlings. Dans le domaine chinois, le livre d’optimisation du professeur Liu Haoyang estime personnellement qu’il est relativement clair et facile à comprendre. Pour ce dernier, tout d'abord, le livre MPC autonome du professeur Gong Jianwei est fortement recommandé. Il y avait des problèmes avec la démo dans l'ancienne version du livre, mais ils ont tous été résolus dans la nouvelle version.
Il existe de nombreux modèles de prédiction utilisés par MPC : tels que le réseau de neurones convolutifs, le contrôle flou, l'espace d'état, etc. Parmi eux, la plus couramment utilisée est la méthode de l'espace d'état. MPC peut être brièvement exprimé comme suit : lorsque les contraintes dynamiques, cinématiques, etc. nécessaires sont remplies, la solution optimale du modèle est résolue par des moyens numériques. La solution optimale est la variable de contrôle de l'équation d'état, telle que l'angle du volant. , etc., et appliquer la quantité de contrôle au modèle de voiture pour obtenir les quantités d'état requises, telles que la vitesse, l'accélération, les coordonnées, etc.
Il ressort de la description ci-dessus que la clé du MPC réside dans l'établissement et la solution du modèle. Comment simplifier de manière équivalente l'établissement du modèle et améliorer l'efficacité de la solution est la priorité absolue. Le véhicule empruntera différentes trajectoires sous différentes entrées de contrôle, et chaque trajectoire correspond à une valeur de fonction objectif. Le véhicule sans pilote utilisera un algorithme de résolution pour trouver la quantité de contrôle correspondant à la valeur de fonction objectif minimale et l'appliquera au véhicule ci-dessus. , comme le montre la figure ci-dessous :
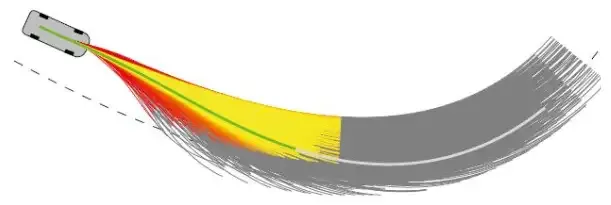
Afin de réduire la difficulté de modélisation, des modèles de champs d'énergie potentielle artificielle sont également utilisés pour la modélisation. L'idée de base des champs d'énergie potentielle artificielle est similaire à celle des champs électriques, et. les obstacles sur la route sont similaires aux sources de champ dans les champs électriques. Charges avec des polarités de charge différentes. L'énergie potentielle aux obstacles (dynamiques, statiques) est plus élevée et le véhicule sans pilote se déplacera vers une position à faible énergie potentielle.
4 Projets Open Source
Recommander un projet open source CppRobotics :
- Planification de chemin
- Dijkstra
- A Star
- RRT
- Approche par fenêtre dynamique
- Générateur de trajectoire prédictive de modèle
- Planificateur de splines cubiques
- State Lattice Planner
- Frenet Frame Trajectory
5 Méthodes d'apprentissage
Le contexte d'apprentissage pour se lancer dans de nouveaux domaines est : Ingénierie, Théorie et Visiontroïka vont de pair, prenant la planification du chemin comme un exemple :
5.1 Engineering
fait référence à la compréhension du contenu de chaque algorithme de planification de chemin, tout en comprenant le contenu de chaque algorithme de la largeur, et en même temps l'apprentissage des détails de chaque algorithme de la profondeur . Concernant les algorithmes dans le domaine de la planification de trajectoire, il n'existe actuellement aucun didacticiel complet, mais la planification de mouvement NMPC de Gong Jianwei peut être une référence.
5.2 Théorie
fait référence à la compréhension des principes mathématiques qui soutiennent le fonctionnement de ces algorithmes et des raisons pour lesquelles ces algorithmes sont générés (perspective mathématique).
- Construire la fonction objectif et les contraintes et trouver la valeur extrême en même temps pour obtenir la variable de contrôle optimale (chemin), qui appartient à la Théorie de l'optimisation
- La méthode commune de Newton, la méthode de descente la plus raide, etc. couramment utilisé lors de la résolution de la variable de contrôle optimale. L'essence de ces méthodes de résolution numérique provient de la résolution numérique d'équations algébriques et appartient à l'analyse numérique
- la matrice jacobienne dérivée vue dans le processus de résolution, la norme vectorielle dans la condition de jugement, etc., consistent essentiellement à convertir une solution numérique unidimensionnelle atteignant des dimensions élevées et appartient à la théorie des matrices.
5.3 Vision
fait référence à la compréhension des principales applications de la planification de parcours dans la recherche scientifique et les entreprises, à l'aide de documents de recherche scientifique et de rapports de résultats, etc.
6 Résumé
Cet article présente les grandes lignes de la planification actuelle des chemins et comprend les méthodes actuelles de planification des chemins. Le contenu est très complexe et il est difficile de tout apprendre en peu de temps sans une orientation pratique vers les applications. Vous ne pouvez vous concentrer sur l'apprentissage qu'en cas de besoin.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Pourquoi le Gaussian Splatting est-il si populaire dans la conduite autonome que le NeRF commence à être abandonné ?
Jan 17, 2024 pm 02:57 PM
Pourquoi le Gaussian Splatting est-il si populaire dans la conduite autonome que le NeRF commence à être abandonné ?
Jan 17, 2024 pm 02:57 PM
Écrit ci-dessus et compréhension personnelle de l'auteur Le Gaussiansplatting tridimensionnel (3DGS) est une technologie transformatrice qui a émergé dans les domaines des champs de rayonnement explicites et de l'infographie ces dernières années. Cette méthode innovante se caractérise par l’utilisation de millions de gaussiennes 3D, ce qui est très différent de la méthode du champ de rayonnement neuronal (NeRF), qui utilise principalement un modèle implicite basé sur les coordonnées pour mapper les coordonnées spatiales aux valeurs des pixels. Avec sa représentation explicite de scènes et ses algorithmes de rendu différenciables, 3DGS garantit non seulement des capacités de rendu en temps réel, mais introduit également un niveau de contrôle et d'édition de scène sans précédent. Cela positionne 3DGS comme un révolutionnaire potentiel pour la reconstruction et la représentation 3D de nouvelle génération. À cette fin, nous fournissons pour la première fois un aperçu systématique des derniers développements et préoccupations dans le domaine du 3DGS.
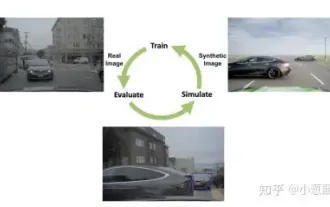 Comment résoudre le problème de la longue traîne dans les scénarios de conduite autonome ?
Jun 02, 2024 pm 02:44 PM
Comment résoudre le problème de la longue traîne dans les scénarios de conduite autonome ?
Jun 02, 2024 pm 02:44 PM
Hier, lors de l'entretien, on m'a demandé si j'avais posé des questions à longue traîne, j'ai donc pensé faire un bref résumé. Le problème à longue traîne de la conduite autonome fait référence aux cas extrêmes dans les véhicules autonomes, c'est-à-dire à des scénarios possibles avec une faible probabilité d'occurrence. Le problème perçu de la longue traîne est l’une des principales raisons limitant actuellement le domaine de conception opérationnelle des véhicules autonomes intelligents à véhicule unique. L'architecture sous-jacente et la plupart des problèmes techniques de la conduite autonome ont été résolus, et les 5 % restants des problèmes à longue traîne sont progressivement devenus la clé pour restreindre le développement de la conduite autonome. Ces problèmes incluent une variété de scénarios fragmentés, de situations extrêmes et de comportements humains imprévisibles. La « longue traîne » des scénarios limites dans la conduite autonome fait référence aux cas limites dans les véhicules autonomes (VA). Les cas limites sont des scénarios possibles avec une faible probabilité d'occurrence. ces événements rares
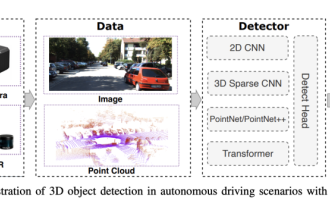 Choisir une caméra ou un lidar ? Une étude récente sur la détection robuste d'objets 3D
Jan 26, 2024 am 11:18 AM
Choisir une caméra ou un lidar ? Une étude récente sur la détection robuste d'objets 3D
Jan 26, 2024 am 11:18 AM
0. Écrit à l'avant&& Compréhension personnelle que les systèmes de conduite autonome s'appuient sur des technologies avancées de perception, de prise de décision et de contrôle, en utilisant divers capteurs (tels que caméras, lidar, radar, etc.) pour percevoir l'environnement et en utilisant des algorithmes et des modèles pour une analyse et une prise de décision en temps réel. Cela permet aux véhicules de reconnaître les panneaux de signalisation, de détecter et de suivre d'autres véhicules, de prédire le comportement des piétons, etc., permettant ainsi de fonctionner en toute sécurité et de s'adapter à des environnements de circulation complexes. Cette technologie attire actuellement une grande attention et est considérée comme un domaine de développement important pour l'avenir des transports. . un. Mais ce qui rend la conduite autonome difficile, c'est de trouver comment faire comprendre à la voiture ce qui se passe autour d'elle. Cela nécessite que l'algorithme de détection d'objets tridimensionnels du système de conduite autonome puisse percevoir et décrire avec précision les objets dans l'environnement, y compris leur emplacement,
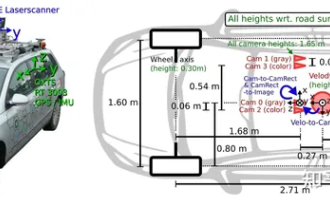 Avez-vous vraiment maîtrisé la conversion des systèmes de coordonnées ? Des enjeux multi-capteurs indispensables à la conduite autonome
Oct 12, 2023 am 11:21 AM
Avez-vous vraiment maîtrisé la conversion des systèmes de coordonnées ? Des enjeux multi-capteurs indispensables à la conduite autonome
Oct 12, 2023 am 11:21 AM
Le premier article pilote et clé présente principalement plusieurs systèmes de coordonnées couramment utilisés dans la technologie de conduite autonome, et comment compléter la corrélation et la conversion entre eux, et enfin construire un modèle d'environnement unifié. L'objectif ici est de comprendre la conversion du véhicule en corps rigide de caméra (paramètres externes), la conversion de caméra en image (paramètres internes) et la conversion d'image en unité de pixel. La conversion de 3D en 2D aura une distorsion, une traduction, etc. Points clés : Le système de coordonnées du véhicule et le système de coordonnées du corps de la caméra doivent être réécrits : le système de coordonnées planes et le système de coordonnées des pixels Difficulté : la distorsion de l'image doit être prise en compte. La dé-distorsion et l'ajout de distorsion sont compensés sur le plan de l'image. 2. Introduction Il existe quatre systèmes de vision au total : système de coordonnées du plan de pixels (u, v), système de coordonnées d'image (x, y), système de coordonnées de caméra () et système de coordonnées mondiales (). Il existe une relation entre chaque système de coordonnées,
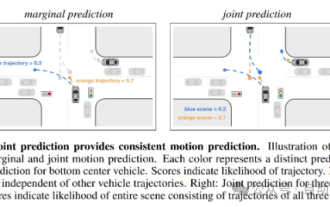 Cet article vous suffit pour en savoir plus sur la conduite autonome et la prédiction de trajectoire !
Feb 28, 2024 pm 07:20 PM
Cet article vous suffit pour en savoir plus sur la conduite autonome et la prédiction de trajectoire !
Feb 28, 2024 pm 07:20 PM
La prédiction de trajectoire joue un rôle important dans la conduite autonome. La prédiction de trajectoire de conduite autonome fait référence à la prédiction de la trajectoire de conduite future du véhicule en analysant diverses données pendant le processus de conduite du véhicule. En tant que module central de la conduite autonome, la qualité de la prédiction de trajectoire est cruciale pour le contrôle de la planification en aval. La tâche de prédiction de trajectoire dispose d'une riche pile technologique et nécessite une connaissance de la perception dynamique/statique de la conduite autonome, des cartes de haute précision, des lignes de voie, des compétences en architecture de réseau neuronal (CNN&GNN&Transformer), etc. Il est très difficile de démarrer ! De nombreux fans espèrent se lancer dans la prédiction de trajectoire le plus tôt possible et éviter les pièges. Aujourd'hui, je vais faire le point sur quelques problèmes courants et des méthodes d'apprentissage introductives pour la prédiction de trajectoire ! Connaissances introductives 1. Existe-t-il un ordre d'entrée pour les épreuves de prévisualisation ? R : Regardez d’abord l’enquête, p
 Parlons des systèmes de conduite autonome de bout en bout et de nouvelle génération, ainsi que de quelques malentendus sur la conduite autonome de bout en bout ?
Apr 15, 2024 pm 04:13 PM
Parlons des systèmes de conduite autonome de bout en bout et de nouvelle génération, ainsi que de quelques malentendus sur la conduite autonome de bout en bout ?
Apr 15, 2024 pm 04:13 PM
Au cours du mois dernier, pour des raisons bien connues, j'ai eu des échanges très intensifs avec divers professeurs et camarades de classe du secteur. Un sujet inévitable dans l'échange est naturellement le populaire Tesla FSDV12 de bout en bout. Je voudrais profiter de cette occasion pour trier certaines de mes pensées et opinions en ce moment pour votre référence et votre discussion. Comment définir un système de conduite autonome de bout en bout et quels problèmes devraient être résolus de bout en bout ? Selon la définition la plus traditionnelle, un système de bout en bout fait référence à un système qui saisit les informations brutes des capteurs et génère directement les variables pertinentes pour la tâche. Par exemple, en reconnaissance d'images, CNN peut être appelé de bout en bout par rapport à la méthode traditionnelle d'extraction de caractéristiques + classificateur. Dans les tâches de conduite autonome, saisir les données de divers capteurs (caméra/LiDAR
 SIMPL : un benchmark de prédiction de mouvement multi-agents simple et efficace pour la conduite autonome
Feb 20, 2024 am 11:48 AM
SIMPL : un benchmark de prédiction de mouvement multi-agents simple et efficace pour la conduite autonome
Feb 20, 2024 am 11:48 AM
Titre original : SIMPL : ASimpleandEfficientMulti-agentMotionPredictionBaselineforAutonomousDriving Lien article : https://arxiv.org/pdf/2402.02519.pdf Lien code : https://github.com/HKUST-Aerial-Robotics/SIMPL Affiliation de l'auteur : Université des sciences de Hong Kong et technologie Idée DJI Paper : cet article propose une base de référence de prédiction de mouvement (SIMPL) simple et efficace pour les véhicules autonomes. Par rapport au cent agent traditionnel
 FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
FisheyeDetNet : le premier algorithme de détection de cible basé sur une caméra fisheye
Apr 26, 2024 am 11:37 AM
La détection de cibles est un problème relativement mature dans les systèmes de conduite autonome, parmi lesquels la détection des piétons est l'un des premiers algorithmes à être déployés. Des recherches très complètes ont été menées dans la plupart des articles. Cependant, la perception de la distance à l’aide de caméras fisheye pour une vue panoramique est relativement moins étudiée. En raison de la distorsion radiale importante, la représentation standard du cadre de délimitation est difficile à mettre en œuvre dans les caméras fisheye. Pour alléger la description ci-dessus, nous explorons les conceptions étendues de boîtes englobantes, d'ellipses et de polygones généraux dans des représentations polaires/angulaires et définissons une métrique de segmentation d'instance mIOU pour analyser ces représentations. Le modèle fisheyeDetNet proposé avec une forme polygonale surpasse les autres modèles et atteint simultanément 49,5 % de mAP sur l'ensemble de données de la caméra fisheye Valeo pour la conduite autonome.





