La rubrique AIxiv de ce site est une rubrique qui publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com.
Dans le domaine de recherche de la modélisation générative 3D, les deux grandes catégories actuelles de méthodes de représentation 3D sont soit basées sur des décodeurs implicites avec des capacités d'ajustement insuffisantes, soit manquent de structures spatiales clairement définies et sont difficiles à intégrer avec la 3D traditionnelle. technologies de diffusion. Des chercheurs de l'Université des sciences et technologies de Chine, de l'Université Tsinghua et de Microsoft Research Asia ont proposé GaussianCube, une représentation 3D explicitement structurée dotée de puissantes capacités d'ajustement, et qui peut être appliquée de manière transparente aux modèles de diffusion 3D traditionnels actuels. GaussianCube commence par un nouvel algorithme d'ajustement gaussien contraint par la densité qui permet un ajustement de haute précision des actifs 3D tout en garantissant l'utilisation d'un nombre fixe de gaussiennes libres. Ces gaussiennes sont ensuite réorganisées dans une grille de voxels prédéfinie à l'aide d'un algorithme de transport optimal. Grâce aux caractéristiques structurelles de GaussianCube, les chercheurs peuvent appliquer directement le standard 3D U-Net comme réseau fédérateur pour la modélisation de diffusion sans conception de réseau complexe. Plus important encore, le nouvel algorithme d'ajustement proposé dans cet article améliore considérablement la compacité de la représentation. Lorsque la qualité d'ajustement de la représentation 3D est similaire, le nombre de paramètres requis n'est que celui requis par une représentation structurée traditionnelle. ou un centième du montant du paramètre. Cette compacité réduit considérablement la complexité de la modélisation générative 3D. Les chercheurs ont mené des expériences approfondies sur la génération d'objets 3D inconditionnelle et conditionnelle, la création d'avatars numériques et la synthèse de contenu texte en 3D. Les résultats numériques montrent que GaussianCube atteint une amélioration des performances allant jusqu'à 74 % par rapport à l'algorithme de base précédent. Comme indiqué ci-dessous, GaussianCube est non seulement capable de générer des ressources 3D de haute qualité, mais fournit également des effets visuels très attrayants, démontrant pleinement son grand potentiel en tant que représentation universelle pour la génération 3D. Figure 1. Résultats générés de manière inconditionnelle. La méthode décrite dans cet article peut générer des modèles 3D diversifiés et de haute qualité.入 Figure 2. Le résultat de la création de l'incarnation numérique basée sur le portrait d'entrée. Le procédé décrit dans cet article peut conserver dans une large mesure les informations sur les caractéristiques d'identité du portrait d'entrée et fournir une modélisation détaillée de la coiffure et des vêtements.入 Figure 3. Les résultats de la création d'actifs 3D basés sur le texte saisi. La méthode décrite dans cet article peut produire des résultats cohérents avec les informations textuelles et modéliser des structures géométriques complexes et des matériaux détaillés. Figure 4. Résultats générés par les conditions de catégorie. Les ressources 3D générées dans cet article ont une sémantique claire et des structures et matériaux géométriques de haute qualité. 
- Nom de l'article : GaussianCube : A Structured and Explicit Radiance Representation for 3D Generative Modeling
- Page d'accueil du projet : https://gaussiancube.github.io/
- Lien de l'article : https://arxiv.org/ pdf/2403.19655
- Code open source : https://github.com/GaussianCube/GaussianCube
- Vidéo de démonstration : https://www.bilibili.com/video/BV1zy411h7wB/
À quel âge utilisez-vous encore le NeRF traditionnel pour la modélisation générative 3D ? La plupart des travaux de modélisation générative 3D précédents ont utilisé une variante du champ de radiance neuronale (NeRF) comme représentation 3D sous-jacente, qui combine généralement une représentation de caractéristiques structurée explicite et un décodeur de caractéristiques implicite. Cependant, dans la modélisation générative 3D, tous les objets 3D doivent partager le même décodeur de caractéristiques implicite, ce qui affaiblit considérablement la capacité d'ajustement de NeRF. De plus, la technologie de rendu de volume sur laquelle s'appuie NeRF présente une complexité de calcul très élevée, ce qui entraîne une vitesse de rendu lente et une consommation de mémoire GPU extrêmement élevée. Récemment, une autre méthode de représentation tridimensionnelle, le 3D Gaussian Splatting (3DGS), a attiré beaucoup d'attention. Bien que 3DGS possède de puissantes capacités d’ajustement, des performances de calcul efficaces et des fonctionnalités entièrement explicites, il a été largement utilisé dans les tâches de reconstruction tridimensionnelle. Cependant, 3DGS ne dispose pas d’une structure spatiale bien définie, ce qui le rend incapable d’être directement appliqué dans les cadres de modélisation générative actuels.
Par conséquent, l'équipe de recherche a proposé GaussianCube. Il s'agit d'une méthode de représentation tridimensionnelle innovante, à la fois structurée et entièrement explicite, dotée de puissantes capacités d'ajustement. La méthode présentée dans cet article garantit d’abord un ajustement de haute précision avec un nombre fixe de gaussiennes libres, puis organise efficacement ces gaussiennes dans une grille de voxels structurée. Cette représentation explicite et structurée permet aux chercheurs d'adopter de manière transparente des architectures de réseau 3D standard, telles que U-Net, sans avoir besoin de réseaux complexes et personnalisés requis lors de l'utilisation de représentations non structurées ou implicitement décodées. Dans le même temps, l'organisation structurée grâce à l'algorithme de transmission optimal maintient au maximum la relation de structure spatiale entre les noyaux gaussiens adjacents, permettant aux chercheurs d'extraire efficacement des caractéristiques en utilisant uniquement des réseaux convolutifs 3D classiques. Plus important encore, compte tenu des résultats d'études précédentes selon lesquels les modèles de diffusion fonctionnent mal lorsqu'il s'agit de distributions de données de grande dimension, le GaussianCube proposé dans cet article réduit considérablement le nombre de paramètres requis tout en maintenant une reconstruction de haute qualité, ce qui atténue considérablement le problème. Il élimine la pression des modèles de diffusion sur la modélisation de distribution et apporte des capacités de modélisation significatives et des améliorations d'efficacité dans le domaine de la modélisation générative 3D.  Présentation du framework GaussianCube
Présentation du framework GaussianCube
Le cadre de cet article se compose de deux étapes principales : la construction de la représentation et la diffusion tridimensionnelle. Dans la phase de construction de la représentation, étant donné un rendu multi-vues d'un actif 3D, un ajustement gaussien contraint par la densité est effectué sur celui-ci pour obtenir un gaussien 3D avec un nombre fixe. Par la suite, la Gaussienne tridimensionnelle est structurée en un GaussianCube grâce à un transfert optimisé. Au cours de l’étape de diffusion 3D, les chercheurs ont entraîné le modèle de diffusion 3D pour générer des GaussianCubes à partir du bruit gaussien. de créez des représentations pour chaque actif 3D adaptées à la modélisation générative. Étant donné que le domaine génératif nécessite souvent que les données modélisées aient une longueur fixe uniforme, le contrôle adaptatif de la densité dans l'algorithme d'ajustement 3DGS original conduira à différents nombres de noyaux gaussiens utilisés pour ajuster différents objets, ce qui pose de grands problèmes à la modélisation générative. Une solution très simple consisterait simplement à supprimer le contrôle adaptatif de la densité, mais les chercheurs ont constaté que cela réduisait considérablement la précision de l’ajustement. Cet article propose un nouvel algorithme d'ajustement de contraintes de densité qui conserve l'opération d'élagage dans le contrôle adaptatif de densité d'origine, mais effectue un nouveau traitement de contraintes sur les opérations de division et de clonage.
Plus précisément, en supposant que l'itération actuelle inclut Gaussiennes, les chercheurs identifient les candidats aux opérations de fractionnement ou de clonage en sélectionnant les gaussiennes dont l'amplitude du gradient à la position spatiale du point de vue dépasse un seuil prédéfini τ, le nombre de ces candidats étant marqué comme
. Afin d'éviter de dépasser le maximum prédéfini de Gaussiennes, les
Gaussiennes ayant le plus grand gradient de position spatiale du point de vue sont sélectionnées parmi les candidats au fractionnement ou au clonage. Après avoir terminé le processus d'ajustement, les chercheurs l'ont rempli de gaussiennes avec α=0 pour atteindre le nombre cible
sans affecter les résultats du rendu. Grâce à cette stratégie, une représentation de haute qualité avec plusieurs ordres de grandeur de paramètres en moins par rapport aux travaux existants de qualité similaire peut être obtenue, réduisant considérablement la difficulté de modélisation des modèles de diffusion. 

 , la gaussienne obtenue grâce à l'algorithme d'ajustement ci-dessus n'a toujours pas de structure d'arrangement spatial claire, ce qui rend le modèle de diffusion ultérieur incapable de modéliser efficacement les données. À cette fin, les chercheurs ont proposé de cartographier les gaussiennes dans une grille de voxels structurée prédéfinie afin de leur donner une structure spatiale claire. Intuitivement, le but de cette étape est de « déplacer » chaque gaussienne dans un voxel tout en conservant autant que possible la contiguïté spatiale des gaussiennes. Les chercheurs l'ont modélisé comme un problème de transmission optimal, ont utilisé l'algorithme de Jonker-Volgenant pour obtenir la relation de cartographie correspondante, puis ont organisé les Gaussiens en voxels correspondants selon la solution de transmission optimale pour obtenir GaussianCube, et remplace la position de la gaussienne originale avec le décalage du centre du voxel actuel pour réduire l'espace de solution du modèle de diffusion. La représentation finale du GaussianCube est non seulement structurée, mais maintient également dans la plus grande mesure la relation structurelle entre les Gaussiennes adjacentes, ce qui fournit un support solide pour une extraction efficace des caractéristiques pour la modélisation générative 3D.
, la gaussienne obtenue grâce à l'algorithme d'ajustement ci-dessus n'a toujours pas de structure d'arrangement spatial claire, ce qui rend le modèle de diffusion ultérieur incapable de modéliser efficacement les données. À cette fin, les chercheurs ont proposé de cartographier les gaussiennes dans une grille de voxels structurée prédéfinie afin de leur donner une structure spatiale claire. Intuitivement, le but de cette étape est de « déplacer » chaque gaussienne dans un voxel tout en conservant autant que possible la contiguïté spatiale des gaussiennes. Les chercheurs l'ont modélisé comme un problème de transmission optimal, ont utilisé l'algorithme de Jonker-Volgenant pour obtenir la relation de cartographie correspondante, puis ont organisé les Gaussiens en voxels correspondants selon la solution de transmission optimale pour obtenir GaussianCube, et remplace la position de la gaussienne originale avec le décalage du centre du voxel actuel pour réduire l'espace de solution du modèle de diffusion. La représentation finale du GaussianCube est non seulement structurée, mais maintient également dans la plus grande mesure la relation structurelle entre les Gaussiennes adjacentes, ce qui fournit un support solide pour une extraction efficace des caractéristiques pour la modélisation générative 3D. Dans l'étape de diffusion tridimensionnelle, cet article utilise un modèle de diffusion tridimensionnelle pour modéliser la distribution de GaussianCube. Grâce à l'organisation spatialement structurée de GaussianCube, la convolution 3D standard est suffisante pour extraire et agréger efficacement les caractéristiques des Gaussiennes voisines sans avoir besoin de conceptions de réseau ou de formation complexes. Par conséquent, les chercheurs ont tiré parti de la diffusion réseau U-Net standard et ont directement remplacé les opérateurs 2D d’origine (y compris la convolution, l’attention, le suréchantillonnage et le sous-échantillonnage) par leurs implémentations 3D.
Le modèle de diffusion tridimensionnelle de cet article prend également en charge une variété de signaux de condition pour contrôler le processus de génération, notamment la génération de conditions d'étiquette de catégorie, la création d'avatars numériques basés sur les conditions de l'image et la génération d'actifs numériques tridimensionnels basés sur texte. La capacité de génération basée sur des conditions multimodales élargit considérablement le champ d'application du modèle et constitue un outil puissant pour la future création de contenu 3D.
Les chercheurs ont d'abord vérifié la capacité d'ajustement de GaussianCube sur l'ensemble de données ShapeNet Car. Les résultats expérimentaux montrent que par rapport aux méthodes de base, GaussianCube peut réaliser un ajustement d'objet tridimensionnel de haute précision à la vitesse la plus rapide et avec le plus petit nombre de paramètres.
Tableau 1. Comparaison numérique de différentes représentations tridimensionnelles sur ShapeNet Car concernant la structure spatiale, la qualité de l'ajustement, la vitesse d'ajustement relative et la quantité de paramètres utilisés.
∗
indique que différents objets partagent des décodeurs de fonctionnalités implicites. Toutes les méthodes sont évaluées avec 30 000 itérations. Figure 8. Comparaison visuelle des capacités d'ajustement de différentes représentations 3D sur ShapeNet Car. ∗ indique que différents objets partagent des décodeurs de caractéristiques implicites. Toutes les méthodes sont évaluées avec 30 000 itérations. 
Les chercheurs ont ensuite vérifié la capacité de génération du modèle de diffusion basé sur GaussianCube sur un grand nombre d'ensembles de données, notamment ShapeNet, OmniObject3D, l'ensemble de données d'avatar numérique synthétique et l'ensemble de données Objaverse. Les résultats expérimentaux montrent que notre modèle obtient des résultats de premier plan en matière de génération d'objets inconditionnels et conditionnés par catégorie, de création d'avatars numériques et de synthèse texte en 3D, allant des métriques numériques à la qualité visuelle. En particulier, GaussianCube atteint une amélioration des performances allant jusqu'à 74 % par rapport à l'algorithme de base précédent. Tableau 2. Comparaison quantitative de la génération inconditionnelle sur ShapeNet Car, Chair et catégorie conditionnelle sur OmniObject3D.

Figure 9. Comparaison qualitative de la génération inconditionnelle sur la forme Voiture nette, chaise. La méthode décrite dans cet article peut générer une géométrie précise et des matériaux détaillés. Figure 10. Comparaison qualitative de la génération de conditions de catégorie sur OmniObject3D. Cette méthode permet de générer des objets complexes avec une sémantique claire. 
. Figure 11. Comparaison qualitative de la création d'avatars numériques basée sur des portraits saisis. La méthode décrite dans cet article permet de restaurer plus précisément les caractéristiques d'identité, les expressions, les accessoires et les détails capillaires du portrait d'entrée. 
Tableau 4. Comparaison quantitative de la création d'actifs 3D basée sur le texte saisi. Le temps d'inférence a été testé à l'aide d'un seul A100. Shap-E et LGM ont obtenu des scores CLIP similaires à ceux de la méthode décrite dans cet article, mais ils ont respectivement utilisé des millions de données d'entraînement (cet article n'a utilisé que 100 000 données tridimensionnelles pour l'entraînement) et un modèle de diffusion de graphes vincentiens bidimensionnels auparavant. Figure 12. Comparaison qualitative de la création d'actifs 3D basée sur le texte saisi. La méthode décrite dans cet article permet de générer des ressources 3D de haute qualité basées sur le texte saisi. Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 Périphériques technologiques
Périphériques technologiques
 IA
IA
 L'épisode le plus prometteur pour la génération 3D de haute qualité ? GaussianCube surpasse largement NeRF en génération 3D
L'épisode le plus prometteur pour la génération 3D de haute qualité ? GaussianCube surpasse largement NeRF en génération 3D


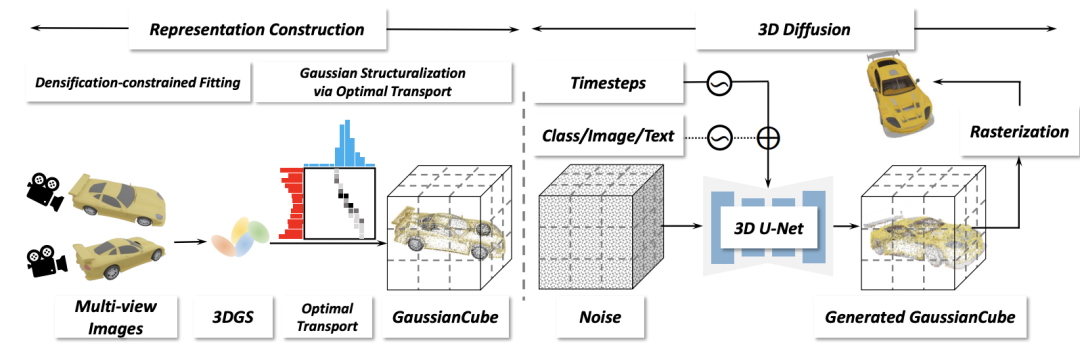 Présentation du framework GaussianCube
Présentation du framework GaussianCube
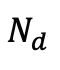
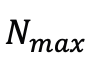 , la gaussienne obtenue grâce à l'algorithme d'ajustement ci-dessus n'a toujours pas de structure d'arrangement spatial claire, ce qui rend le modèle de diffusion ultérieur incapable de modéliser efficacement les données. À cette fin, les chercheurs ont proposé de cartographier les gaussiennes dans une grille de voxels structurée prédéfinie afin de leur donner une structure spatiale claire. Intuitivement, le but de cette étape est de « déplacer » chaque gaussienne dans un voxel tout en conservant autant que possible la contiguïté spatiale des gaussiennes.
, la gaussienne obtenue grâce à l'algorithme d'ajustement ci-dessus n'a toujours pas de structure d'arrangement spatial claire, ce qui rend le modèle de diffusion ultérieur incapable de modéliser efficacement les données. À cette fin, les chercheurs ont proposé de cartographier les gaussiennes dans une grille de voxels structurée prédéfinie afin de leur donner une structure spatiale claire. Intuitivement, le but de cette étape est de « déplacer » chaque gaussienne dans un voxel tout en conservant autant que possible la contiguïté spatiale des gaussiennes. 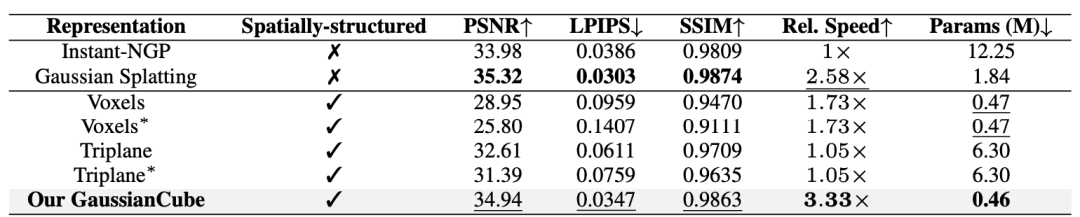

















 Le robot DeepMind joue au tennis de table, et son coup droit et son revers glissent dans les airs, battant complètement les débutants humains
Aug 09, 2024 pm 04:01 PM
Le robot DeepMind joue au tennis de table, et son coup droit et son revers glissent dans les airs, battant complètement les débutants humains
Aug 09, 2024 pm 04:01 PM
 Claude aussi est devenu paresseux ! Internaute : apprenez à vous accorder des vacances
Sep 02, 2024 pm 01:56 PM
Claude aussi est devenu paresseux ! Internaute : apprenez à vous accorder des vacances
Sep 02, 2024 pm 01:56 PM
 La première griffe mécanique ! Yuanluobao est apparu à la World Robot Conference 2024 et a lancé le premier robot d'échecs pouvant entrer dans la maison
Aug 21, 2024 pm 07:33 PM
La première griffe mécanique ! Yuanluobao est apparu à la World Robot Conference 2024 et a lancé le premier robot d'échecs pouvant entrer dans la maison
Aug 21, 2024 pm 07:33 PM
 Lors de la World Robot Conference, ce robot domestique porteur de « l'espoir des futurs soins aux personnes âgées » a été entouré
Aug 22, 2024 pm 10:35 PM
Lors de la World Robot Conference, ce robot domestique porteur de « l'espoir des futurs soins aux personnes âgées » a été entouré
Aug 22, 2024 pm 10:35 PM
 L'équipe de Li Feifei a proposé ReKep pour donner aux robots une intelligence spatiale et intégrer GPT-4o
Sep 03, 2024 pm 05:18 PM
L'équipe de Li Feifei a proposé ReKep pour donner aux robots une intelligence spatiale et intégrer GPT-4o
Sep 03, 2024 pm 05:18 PM
 Annonce des prix ACL 2024 : l'un des meilleurs articles sur le déchiffrement Oracle par HuaTech, GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
Annonce des prix ACL 2024 : l'un des meilleurs articles sur le déchiffrement Oracle par HuaTech, GloVe Time Test Award
Aug 15, 2024 pm 04:37 PM
 Hongmeng Smart Travel S9 et conférence de lancement de nouveaux produits avec scénario complet, un certain nombre de nouveaux produits à succès ont été lancés ensemble
Aug 08, 2024 am 07:02 AM
Hongmeng Smart Travel S9 et conférence de lancement de nouveaux produits avec scénario complet, un certain nombre de nouveaux produits à succès ont été lancés ensemble
Aug 08, 2024 am 07:02 AM
 Le premier grand modèle d'interface utilisateur en Chine est lancé ! Le grand modèle de Motiff crée le meilleur assistant pour les concepteurs et optimise le flux de travail de conception d'interface utilisateur
Aug 19, 2024 pm 04:48 PM
Le premier grand modèle d'interface utilisateur en Chine est lancé ! Le grand modèle de Motiff crée le meilleur assistant pour les concepteurs et optimise le flux de travail de conception d'interface utilisateur
Aug 19, 2024 pm 04:48 PM





