 Périphériques technologiques
Périphériques technologiques
 IA
IA
 J'ai hâte de voir Q* d'OpenAI, l'arme secrète de Huawei Noah, MindStar pour explorer le raisonnement LLM, est là en premier
J'ai hâte de voir Q* d'OpenAI, l'arme secrète de Huawei Noah, MindStar pour explorer le raisonnement LLM, est là en premier
J'ai hâte de voir Q* d'OpenAI, l'arme secrète de Huawei Noah, MindStar pour explorer le raisonnement LLM, est là en premier

La rubrique AIxiv est une rubrique où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com

Titre de l'article : MindStar : Enhancing Math Reasoning in Pre-trained LLMs at Inference Time Adresse de l'article : https://arxiv.org/abs/2405.16265v2

Le rapport Llama-3 [10] met en évidence une observation importante : face à un problème d'inférence difficile, les modèles génèrent parfois des trajectoires d'inférence correctes. Cela suggère que le modèle sait comment produire la bonne réponse, mais qu’il a du mal à la sélectionner. Sur la base de ces résultats, nous avons posé une question simple : pouvons-nous améliorer les capacités de raisonnement des LLM en les aidant à choisir le bon résultat ? Pour explorer cela, nous avons mené une expérience en utilisant différents modèles de récompense pour la sélection des résultats des LLM. Les résultats expérimentaux montrent que la sélection par étapes surpasse considérablement les méthodes CoT traditionnelles.
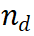 PRM évalue les nouvelles étapes en considérant l'ensemble de la trajectoire de raisonnement actuelle, en encourageant la cohérence et la fidélité au cheminement global. Une valeur de récompense élevée indique que la nouvelle étape
PRM évalue les nouvelles étapes en considérant l'ensemble de la trajectoire de raisonnement actuelle, en encourageant la cohérence et la fidélité au cheminement global. Une valeur de récompense élevée indique que la nouvelle étape 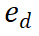 ) est probablement correcte pour un chemin de raisonnement donné
) est probablement correcte pour un chemin de raisonnement donné 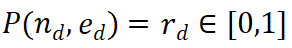 , ce qui rend le chemin d'expansion intéressant une exploration plus approfondie. À l’inverse, une valeur de récompense faible indique que la nouvelle étape peut être incorrecte, ce qui signifie que la solution qui suit ce chemin peut également être incorrecte. L'algorithme
, ce qui rend le chemin d'expansion intéressant une exploration plus approfondie. À l’inverse, une valeur de récompense faible indique que la nouvelle étape peut être incorrecte, ce qui signifie que la solution qui suit ce chemin peut également être incorrecte. L'algorithme 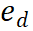
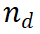
1 Expansion du chemin d'inférence : à chaque itération, le LLM sous-jacent génère l'étape suivante du chemin d'inférence actuel. .
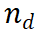 , nous avons conçu un modèle d'invite (exemple 3.1) pour collecter les prochaines étapes du LLM. Comme le montre l'exemple, LLM traite la question d'origine comme {question} et le chemin de raisonnement actuel comme {réponse}. Notez que lors de la première itération de l'algorithme, le nœud sélectionné est le nœud racine qui contient uniquement la question, donc {answer} est vide. Pour un chemin d'inférence
, nous avons conçu un modèle d'invite (exemple 3.1) pour collecter les prochaines étapes du LLM. Comme le montre l'exemple, LLM traite la question d'origine comme {question} et le chemin de raisonnement actuel comme {réponse}. Notez que lors de la première itération de l'algorithme, le nœud sélectionné est le nœud racine qui contient uniquement la question, donc {answer} est vide. Pour un chemin d'inférence  , LLM génère N étapes intermédiaires et les ajoute en tant qu'enfants du nœud actuel. Dans l'étape suivante de l'algorithme, ces nœuds enfants nouvellement générés sont évalués et un nouveau nœud est sélectionné pour une expansion ultérieure. Nous avons également réalisé qu'une autre façon de générer des étapes consiste à affiner le LLM à l'aide de marqueurs d'étape. Cependant, cela peut réduire la capacité d'inférence du LLM et, plus important encore, cela va à l'encontre de l'objectif de cet article : améliorer la capacité d'inférence du LLM sans modifier les pondérations.
, LLM génère N étapes intermédiaires et les ajoute en tant qu'enfants du nœud actuel. Dans l'étape suivante de l'algorithme, ces nœuds enfants nouvellement générés sont évalués et un nouveau nœud est sélectionné pour une expansion ultérieure. Nous avons également réalisé qu'une autre façon de générer des étapes consiste à affiner le LLM à l'aide de marqueurs d'étape. Cependant, cela peut réduire la capacité d'inférence du LLM et, plus important encore, cela va à l'encontre de l'objectif de cet article : améliorer la capacité d'inférence du LLM sans modifier les pondérations. 



Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1674
1674
 14
14
 1429
1429
 52
52
 1333
1333
 25
25
 1278
1278
 29
29
 1257
1257
 24
24
 L'auteur de ControlNet a encore un succès ! L'ensemble du processus de génération d'une peinture à partir d'une image, gagnant 1,4k étoiles en deux jours
Jul 17, 2024 am 01:56 AM
L'auteur de ControlNet a encore un succès ! L'ensemble du processus de génération d'une peinture à partir d'une image, gagnant 1,4k étoiles en deux jours
Jul 17, 2024 am 01:56 AM
Il s'agit également d'une vidéo Tusheng, mais PaintsUndo a emprunté une voie différente. L'auteur de ControlNet, LvminZhang, a recommencé à vivre ! Cette fois, je vise le domaine de la peinture. Le nouveau projet PaintsUndo a reçu 1,4kstar (toujours en hausse folle) peu de temps après son lancement. Adresse du projet : https://github.com/lllyasviel/Paints-UNDO Grâce à ce projet, l'utilisateur saisit une image statique et PaintsUndo peut automatiquement vous aider à générer une vidéo de l'ensemble du processus de peinture, du brouillon de ligne au suivi du produit fini. . Pendant le processus de dessin, les changements de lignes sont étonnants. Le résultat vidéo final est très similaire à l’image originale : jetons un coup d’œil à un dessin complet.
 En tête de liste des ingénieurs logiciels d'IA open source, la solution sans agent de l'UIUC résout facilement les problèmes de programmation réels du banc SWE.
Jul 17, 2024 pm 10:02 PM
En tête de liste des ingénieurs logiciels d'IA open source, la solution sans agent de l'UIUC résout facilement les problèmes de programmation réels du banc SWE.
Jul 17, 2024 pm 10:02 PM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com Les auteurs de cet article font tous partie de l'équipe de l'enseignant Zhang Lingming de l'Université de l'Illinois à Urbana-Champaign (UIUC), notamment : Steven Code repair ; doctorant en quatrième année, chercheur
 Du RLHF au DPO en passant par TDPO, les algorithmes d'alignement des grands modèles sont déjà « au niveau des jetons »
Jun 24, 2024 pm 03:04 PM
Du RLHF au DPO en passant par TDPO, les algorithmes d'alignement des grands modèles sont déjà « au niveau des jetons »
Jun 24, 2024 pm 03:04 PM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com Dans le processus de développement de l'intelligence artificielle, le contrôle et le guidage des grands modèles de langage (LLM) ont toujours été l'un des principaux défis, visant à garantir que ces modèles sont à la fois puissant et sûr au service de la société humaine. Les premiers efforts se sont concentrés sur les méthodes d’apprentissage par renforcement par feedback humain (RL
 Les articles arXiv peuvent être publiés sous forme de 'barrage', la plateforme de discussion alphaXiv de Stanford est en ligne, LeCun l'aime
Aug 01, 2024 pm 05:18 PM
Les articles arXiv peuvent être publiés sous forme de 'barrage', la plateforme de discussion alphaXiv de Stanford est en ligne, LeCun l'aime
Aug 01, 2024 pm 05:18 PM
acclamations! Qu’est-ce que ça fait lorsqu’une discussion sur papier se résume à des mots ? Récemment, des étudiants de l'Université de Stanford ont créé alphaXiv, un forum de discussion ouvert pour les articles arXiv qui permet de publier des questions et des commentaires directement sur n'importe quel article arXiv. Lien du site Web : https://alphaxiv.org/ En fait, il n'est pas nécessaire de visiter spécifiquement ce site Web. Il suffit de remplacer arXiv dans n'importe quelle URL par alphaXiv pour ouvrir directement l'article correspondant sur le forum alphaXiv : vous pouvez localiser avec précision les paragraphes dans. l'article, Phrase : dans la zone de discussion sur la droite, les utilisateurs peuvent poser des questions à l'auteur sur les idées et les détails de l'article. Par exemple, ils peuvent également commenter le contenu de l'article, tels que : "Donné à".
 Travail posthume de l'équipe OpenAI Super Alignment : deux grands modèles jouent à un jeu et le résultat devient plus compréhensible
Jul 19, 2024 am 01:29 AM
Travail posthume de l'équipe OpenAI Super Alignment : deux grands modèles jouent à un jeu et le résultat devient plus compréhensible
Jul 19, 2024 am 01:29 AM
Si la réponse donnée par le modèle d’IA est incompréhensible du tout, oseriez-vous l’utiliser ? À mesure que les systèmes d’apprentissage automatique sont utilisés dans des domaines de plus en plus importants, il devient de plus en plus important de démontrer pourquoi nous pouvons faire confiance à leurs résultats, et quand ne pas leur faire confiance. Une façon possible de gagner confiance dans le résultat d'un système complexe est d'exiger que le système produise une interprétation de son résultat qui soit lisible par un humain ou un autre système de confiance, c'est-à-dire entièrement compréhensible au point que toute erreur possible puisse être trouvé. Par exemple, pour renforcer la confiance dans le système judiciaire, nous exigeons que les tribunaux fournissent des avis écrits clairs et lisibles qui expliquent et soutiennent leurs décisions. Pour les grands modèles de langage, nous pouvons également adopter une approche similaire. Cependant, lorsque vous adoptez cette approche, assurez-vous que le modèle de langage génère
 Une avancée significative dans l'hypothèse de Riemann ! Tao Zhexuan recommande fortement les nouveaux articles du MIT et d'Oxford, et le lauréat de la médaille Fields, âgé de 37 ans, a participé
Aug 05, 2024 pm 03:32 PM
Une avancée significative dans l'hypothèse de Riemann ! Tao Zhexuan recommande fortement les nouveaux articles du MIT et d'Oxford, et le lauréat de la médaille Fields, âgé de 37 ans, a participé
Aug 05, 2024 pm 03:32 PM
Récemment, l’hypothèse de Riemann, connue comme l’un des sept problèmes majeurs du millénaire, a réalisé une nouvelle avancée. L'hypothèse de Riemann est un problème mathématique non résolu très important, lié aux propriétés précises de la distribution des nombres premiers (les nombres premiers sont les nombres qui ne sont divisibles que par 1 et par eux-mêmes, et jouent un rôle fondamental dans la théorie des nombres). Dans la littérature mathématique actuelle, il existe plus d'un millier de propositions mathématiques basées sur l'établissement de l'hypothèse de Riemann (ou sa forme généralisée). En d’autres termes, une fois que l’hypothèse de Riemann et sa forme généralisée seront prouvées, ces plus d’un millier de propositions seront établies sous forme de théorèmes, qui auront un impact profond sur le domaine des mathématiques et si l’hypothèse de Riemann s’avère fausse, alors parmi eux ; ces propositions qui en font partie perdront également de leur efficacité. Une nouvelle percée vient du professeur de mathématiques du MIT, Larry Guth, et de l'Université d'Oxford
 LLM n'est vraiment pas bon pour la prédiction de séries chronologiques. Il n'utilise même pas sa capacité de raisonnement.
Jul 15, 2024 pm 03:59 PM
LLM n'est vraiment pas bon pour la prédiction de séries chronologiques. Il n'utilise même pas sa capacité de raisonnement.
Jul 15, 2024 pm 03:59 PM
Les modèles linguistiques peuvent-ils vraiment être utilisés pour la prédiction de séries chronologiques ? Selon la loi des gros titres de Betteridge (tout titre d'actualité se terminant par un point d'interrogation peut recevoir une réponse « non »), la réponse devrait être non. Le fait semble être vrai : un LLM aussi puissant ne peut pas bien gérer les données de séries chronologiques. Les séries chronologiques, c'est-à-dire les séries chronologiques, comme leur nom l'indique, font référence à un ensemble de séquences de points de données disposées par ordre temporel. L'analyse des séries chronologiques est essentielle dans de nombreux domaines, notamment la prévision de la propagation des maladies, l'analyse du commerce de détail, la santé et la finance. Dans le domaine de l'analyse des séries chronologiques, de nombreux chercheurs ont récemment étudié comment utiliser les grands modèles linguistiques (LLM) pour classer, prédire et détecter les anomalies dans les séries chronologiques. Ces articles supposent que les modèles de langage capables de gérer les dépendances séquentielles dans le texte peuvent également se généraliser aux séries chronologiques.
 Le premier MLLM basé sur Mamba est là ! Les poids des modèles, le code de formation, etc. sont tous open source
Jul 17, 2024 am 02:46 AM
Le premier MLLM basé sur Mamba est là ! Les poids des modèles, le code de formation, etc. sont tous open source
Jul 17, 2024 am 02:46 AM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com. Introduction Ces dernières années, l'application de grands modèles de langage multimodaux (MLLM) dans divers domaines a connu un succès remarquable. Cependant, en tant que modèle de base pour de nombreuses tâches en aval, le MLLM actuel se compose du célèbre réseau Transformer, qui



