
Le modèle gagnant de l'IA Math Olympiad est sorti !
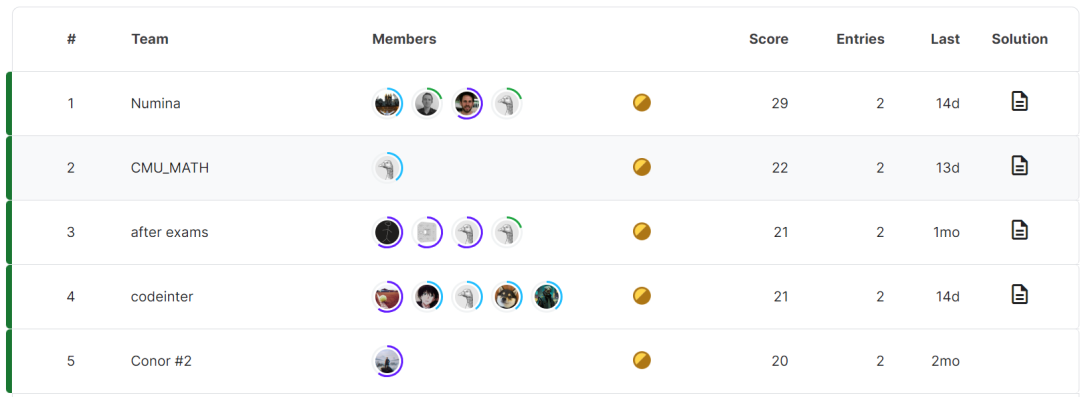
 Tout à l'heure, les modèles derrière les quatre meilleurs AIMO Progress Awards ont été annoncés.
Tout à l'heure, les modèles derrière les quatre meilleurs AIMO Progress Awards ont été annoncés. 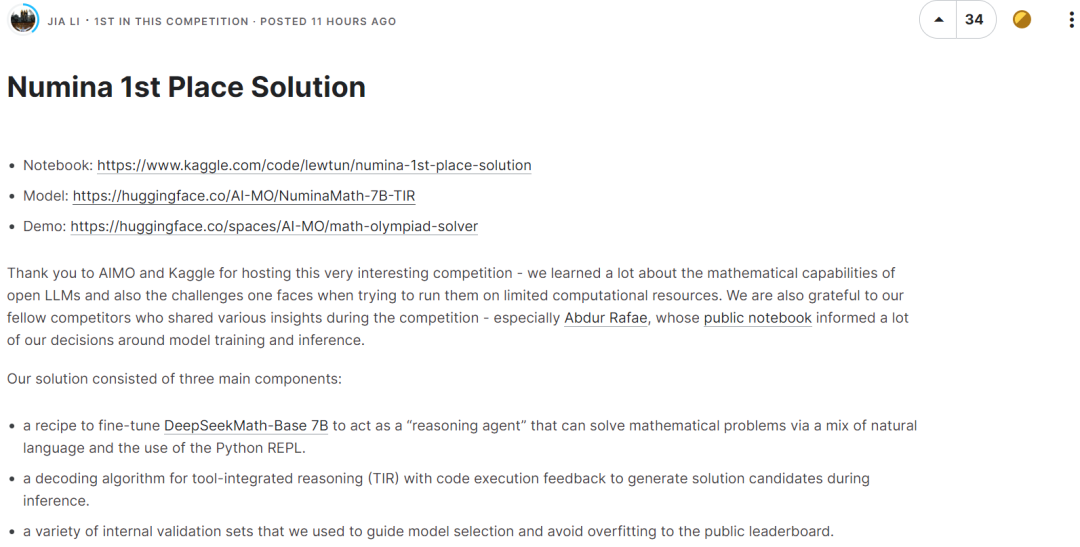 La troisième place a également utilisé le modèle DeepSeek-Math-7B-RL sans aucun réglage fin, et a utilisé une stratégie de vote majoritaire pour sélectionner la bonne réponse via les règles de notation établies.
La troisième place a également utilisé le modèle DeepSeek-Math-7B-RL sans aucun réglage fin, et a utilisé une stratégie de vote majoritaire pour sélectionner la bonne réponse via les règles de notation établies. 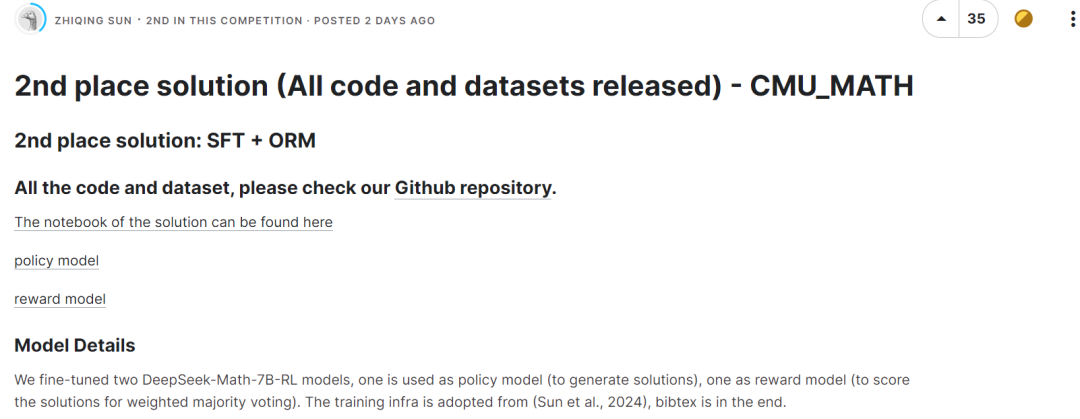 L'équipe classée quatrième a également utilisé deepseek-math-7b-rl, avec des paramètres de température de 0,9, top_p de 1,0 et un maximum de jetons de 2048. Associé à des outils de codage, ce modèle atteint 58,8 % sur le benchmark MATH.
L'équipe classée quatrième a également utilisé deepseek-math-7b-rl, avec des paramètres de température de 0,9, top_p de 1,0 et un maximum de jetons de 2048. Associé à des outils de codage, ce modèle atteint 58,8 % sur le benchmark MATH. 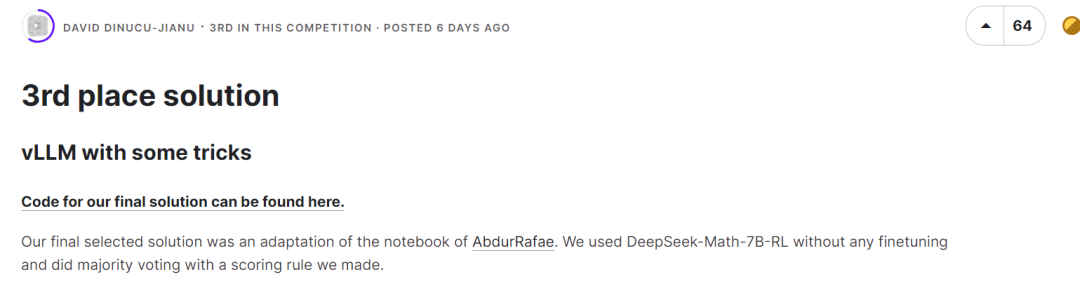 Il n'est pas difficile de constater que les quatre meilleures équipes ont toutes choisi DeepSeekMath-7B comme modèle de base et ont obtenu de bons résultats. La capacité de raisonnement mathématique de ce modèle est proche de celle de GPT-4, dépassant un certain nombre de modèles open source 30B ~ 70B sur la liste de référence MATH.
Il n'est pas difficile de constater que les quatre meilleures équipes ont toutes choisi DeepSeekMath-7B comme modèle de base et ont obtenu de bons résultats. La capacité de raisonnement mathématique de ce modèle est proche de celle de GPT-4, dépassant un certain nombre de modèles open source 30B ~ 70B sur la liste de référence MATH. 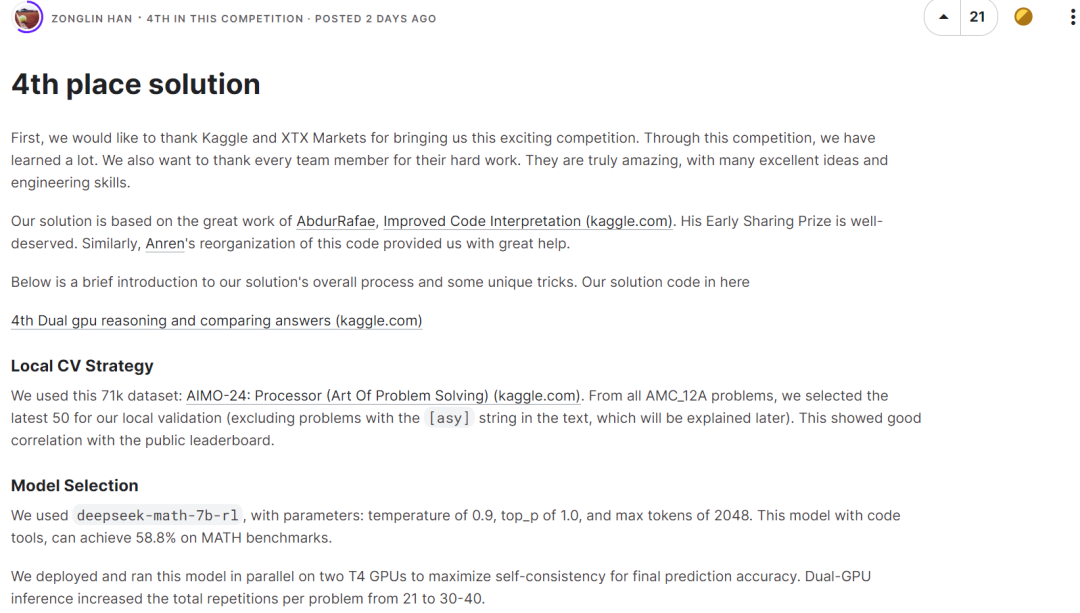
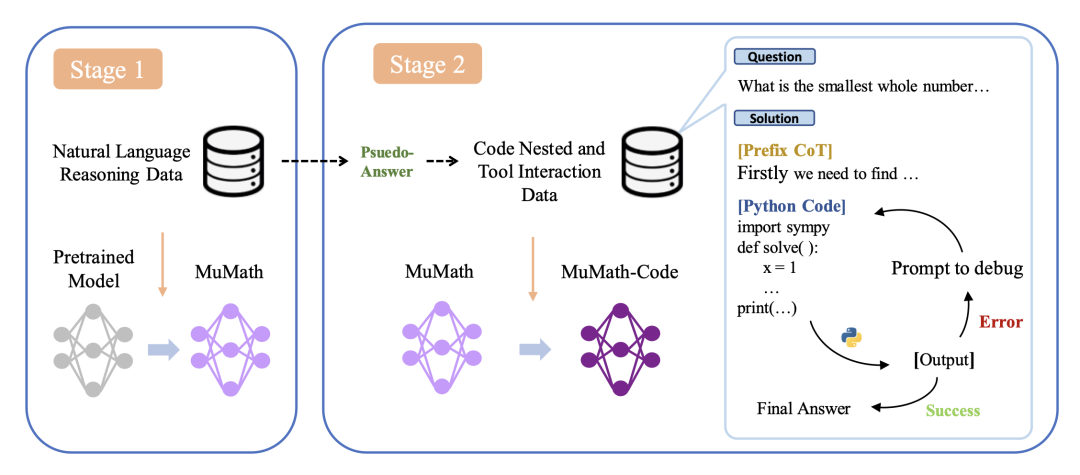
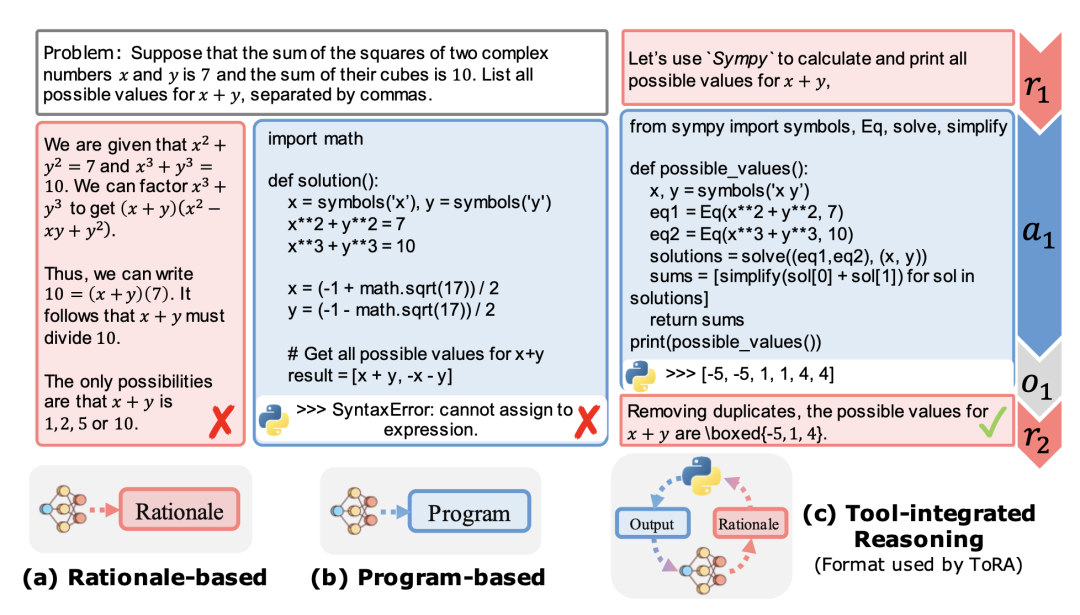
 NuminaMath 7B TIR est une version affinée de deepseek-math-7b-base avec deux étapes de réglage fin supervisé :
NuminaMath 7B TIR est une version affinée de deepseek-math-7b-base avec deux étapes de réglage fin supervisé : 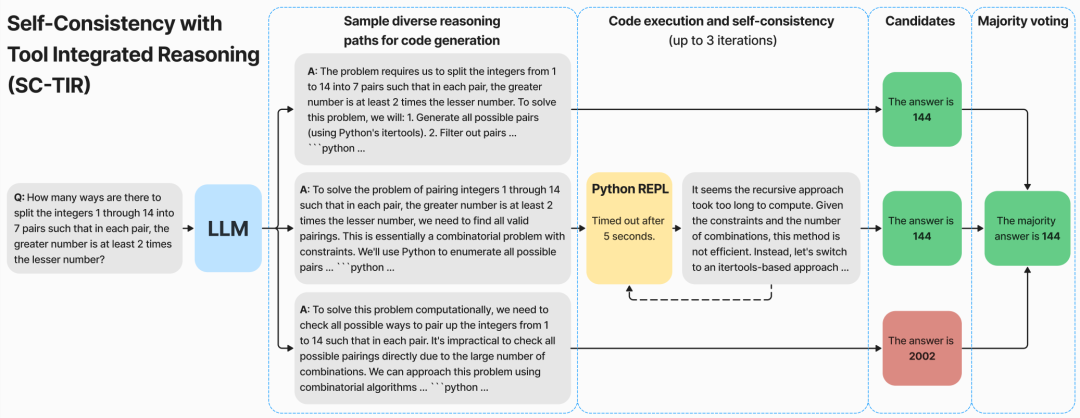
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!
 gt540
gt540
 js actualiser la page actuelle
js actualiser la page actuelle
 git pull extrait le code
git pull extrait le code
 Comment acheter de vraies pièces Ripple
Comment acheter de vraies pièces Ripple
 Comment résoudre le crash du Webstorm
Comment résoudre le crash du Webstorm
 Comparez les similitudes et les différences entre deux colonnes de données dans Excel
Comparez les similitudes et les différences entre deux colonnes de données dans Excel
 Comment éliminer le code HTML
Comment éliminer le code HTML
 Que sont les logiciels de programmation en langage C ?
Que sont les logiciels de programmation en langage C ?