Débloquez le potentiel de faire évoluer Transformer davantage tout en maintenant l'efficacité informatique. Les couches Feedforward (FFW) de l'architecture Transformer standard entraînent une augmentation linéaire du coût de calcul et de la mémoire d'activation à mesure que la largeur de la couche cachée augmente. Alors que la taille des grands modèles de langage (LLM) continue d’augmenter, l’architecture Sparse Mixed Expert (MoE) est devenue une méthode réalisable pour résoudre ce problème, qui sépare la taille du modèle du coût de calcul. De nombreux modèles MoE émergents peuvent atteindre de meilleures performances et des performances plus puissantes pour la même taille.
La loi récemment découverte de l'expansion du MoE à granularité fine montre qu'une granularité plus élevée conduit à de meilleures performances. Cependant, les modèles MoE existants sont limités à un petit nombre d’experts en raison de problèmes de calcul et d’optimisation. Une nouvelle recherche de Google DeepMind présente un mécanisme de récupération d'experts efficace en termes de paramètres qui exploite la technologie clé du produit pour effectuer une récupération éparse auprès d'un million de micro-experts
Lien : https://arxiv.org/abs/2407.04153 Cette approche tente de découpler le coût de calcul du nombre de paramètres en concaténant efficacement un grand nombre de petits experts via une structure d'index apprise pour routage . Démontre une efficacité supérieure par rapport aux couches denses FFW, MoE à gros grains et Product Key Memory (PKM).
Cette approche tente de découpler le coût de calcul du nombre de paramètres en concaténant efficacement un grand nombre de petits experts via une structure d'index apprise pour routage . Démontre une efficacité supérieure par rapport aux couches denses FFW, MoE à gros grains et Product Key Memory (PKM).
Ce travail présente l'architecture PEER (Parameter Efficient Expert Retrieval) (récupération experte efficace des paramètres), qui utilise la récupération de clé de produit pour acheminer efficacement vers un grand nombre d'experts, en séparant le coût de calcul de la quantité de paramètres. Cette conception a démontré des niveaux de performances informatiques supérieurs lors des expériences, la positionnant comme une alternative compétitive aux couches FFW denses pour étendre les modèles de base. Les principales contributions de ce travail sont :
Exploration des paramètres extrêmes du MoE : contrairement à l'accent mis sur quelques grands experts dans les études précédentes du MoE, ce travail étudie la situation sous-explorée de nombreux petits experts.
Structure d'index apprise pour le routage : première démonstration qu'une structure d'index apprise peut acheminer efficacement vers plus d'un million d'experts.
Nouvelle conception de couche : en combinant le routage des clés de produit avec des experts en neurones uniques, nous introduisons la couche PEER, qui adapte la capacité de la couche sans surcharge de calcul significative. Les résultats empiriques démontrent une efficacité supérieure par rapport aux couches denses FFW, MoE à gros grains et Product Key Memory (PKM).
Étude complète d'ablation : nous étudions l'impact de différents choix de conception pour PEER (tels que le nombre d'experts, les paramètres d'activité, le nombre de têtes et la normalisation des lots de requêtes) sur les tâches de modélisation du langage. Introduction à la méthode
Dans cette section, le chercheur explique en détail la couche PEER (Parametric Efficient Expert Retrieval), une architecture experte hybride qui utilise des clés de produit dans le routage et le MLP à neurone unique. expert. La figure 2 ci-dessous montre le processus de calcul au sein de la couche PEER. Aperçu de la couche PEER
. Formellement, la couche PEER est une fonction f : R^n → R^m, qui se compose de trois parties : un pool de N experts E := {e_i}^N_i=1, où chaque expert e_i : R^n → R ^m partage la même signature que f ; un ensemble correspondant de N clés de produit K := {k_i}^N_i=1 ⊂ R^d et un réseau de requêtes q : R^n → R ^d ; x ∈ R^n au vecteur de requête q (x). 
Laissez T_k représenter l'opérateur top-k. Étant donné une entrée x, récupérez d'abord le sous-ensemble de k experts dont les clés de produit correspondantes ont le produit interne le plus élevé avec la requête q (x). Appliquez ensuite une activation non linéaire (telle que softmax ou sigmoïde) au produit interne de la clé de requête des k meilleurs experts pour obtenir le score de routage.  Enfin, le résultat est calculé en combinant linéairement les résultats des experts pondérés par les scores de routage.
Enfin, le résultat est calculé en combinant linéairement les résultats des experts pondérés par les scores de routage.
Récupération de clé de produit. Étant donné que les chercheurs ont l'intention de faire appel à un grand nombre d'experts (N ≥ 10^6), le simple calcul des k premiers indices dans l'équation 1 peut être très coûteux, c'est pourquoi la technique de récupération de clé de produit est appliquée. Au lieu d'utiliser N vecteurs d-dimensionnels indépendants comme clés k_i, ils les créent en concaténant des vecteurs à partir de deux ensembles de sous-clés indépendants d/2 dimensions (c'est-à-dire C, C ′ ⊂ R d/2) :

Paramétrique recherche efficace d'experts et multi-têtes. Contrairement aux autres architectures MoE, ces architectures définissent généralement la couche cachée de chaque expert à la même taille que les autres couches FFW. Dans PEER, chaque expert e_i est un MLP singleton, en d'autres termes, il n'a qu'une seule couche cachée avec un seul neurone : 
Les chercheurs n'ont pas modifié la taille de l'expert individuel, mais ont utilisé la récupération multi-têtes. utilisé pour ajuster la capacité d'expression de la couche PEER, qui est similaire au mécanisme d'attention multi-têtes du transformateur et à la mémoire multi-têtes du PKM. Plus précisément, ils utilisent h réseaux de requêtes indépendants, chaque réseau calcule sa propre requête et récupère un ensemble distinct de k experts. Cependant, différents responsables partagent le même pool d’experts, avec le même ensemble de clés de produit. Le résultat de ces têtes h se résume simplement comme suit : 
Pourquoi avons-nous besoin d'un grand nombre de petits experts ? Une couche MoE donnée peut être caractérisée par trois hyperparamètres : le nombre total de paramètres P, le nombre de paramètres actifs par jeton P_active et la taille d'un seul expert P_expert. Krajewski et al. (2024) ont montré que la loi d'échelle du modèle MoE a la forme suivante : 
Pour PEER, le chercheur utilise la plus petite taille d'expert possible en définissant d_expert = 1, et le nombre de neurones activés est la tête de recherche Le nombre est multiplié par le nombre d'experts récupérés par tête : d_active = hk. Par conséquent, la granularité de PEER est toujours G = P_active/P_expert = d_active/d_expert = hk. 
Regardons d'abord les résultats de l'évaluation sur l'ensemble de données de modélisation du langage. Après avoir déterminé le modèle informatique optimal pour chaque méthode sur la base de la courbe isoFLOP, les chercheurs ont évalué les performances de ces modèles pré-entraînés sur les ensembles de données de modélisation de langage populaires suivants :
- Ensemble de données de pré-formation C4
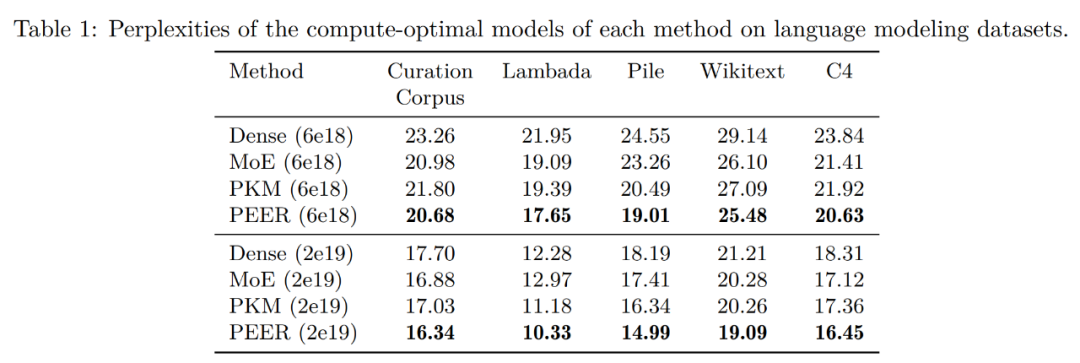
Le tableau 1 ci-dessous montre les résultats de l'évaluation. Les chercheurs ont regroupé les modèles en fonction du budget FLOP utilisé lors de la formation. Comme on peut le voir, PEER a le moins de perplexité sur ces ensembles de données de modélisation linguistique. 
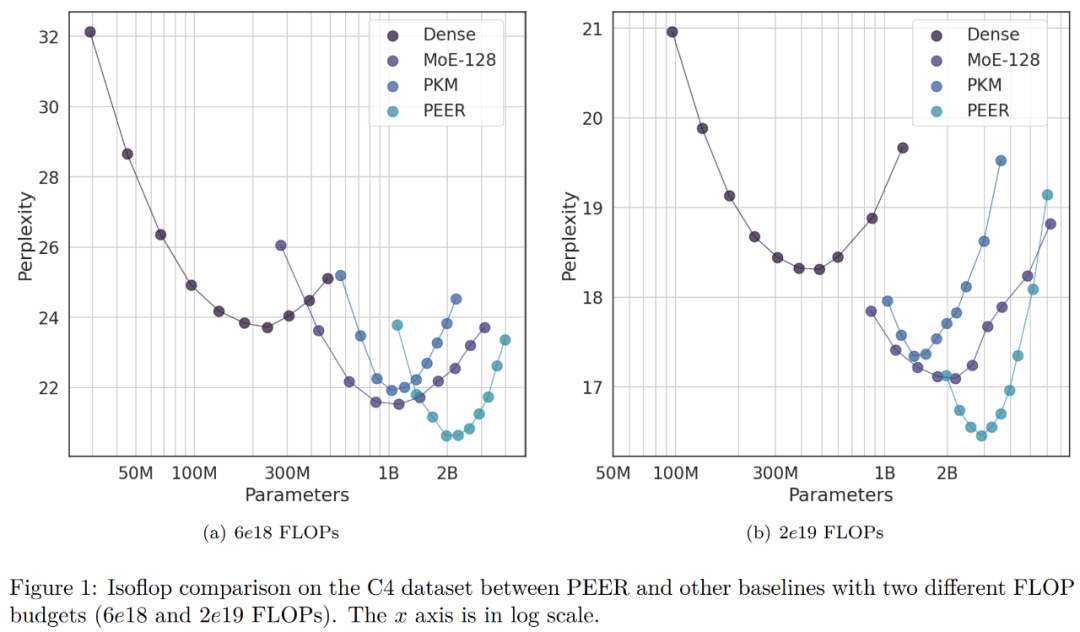
Dans l'expérience d'ablation, les chercheurs ont modifié le nombre total d'experts. Les modèles présentés dans la courbe isoFLOP de la figure 1 ci-dessous comptent tous plus d'un million (1 024 ^ 2) d'experts. 
Le chercheur a choisi le modèle avec la position optimale d'isoFLOP et a modifié le nombre d'experts dans la couche PEER (N = 128^2, 256^2, 512^2, 1024^2), tout en gardant le nombre d'experts actifs inchangé. (h = 8, k = 16). Les résultats sont présentés dans la figure 3 (a) ci-dessous. On peut voir que la courbe isoFLOP interpole entre le modèle PEER avec 1024^2 experts et le squelette dense correspondant sans remplacer la couche FFW du bloc central par une couche PEER. Cela montre que les performances du modèle peuvent être améliorées simplement en augmentant le nombre d’experts. Dans le même temps, les chercheurs ont modifié le nombre d'experts actifs. Ils ont systématiquement fait varier le nombre d'experts actifs (hk = 32, 64, 128, 256, 512) tout en gardant constant le nombre total d'experts (N = 1024^2). Pour un hk donné, le chercheur modifie ensuite conjointement h et k pour déterminer la meilleure combinaison. La figure 3 (b) ci-dessous représente la courbe isoFLOP par rapport au nombre de têtes (h). 
Le tableau 2 ci-dessous répertorie l'utilisation des experts et les inégalités pour différents nombres d'experts avec et sans BN. On peut voir que même pour 1 million d'experts, le taux d'utilisation des experts est proche de 100 %, et l'utilisation de BN peut rendre le taux d'utilisation des experts plus équilibré et le niveau de confusion plus faible. Ces résultats démontrent l’efficacité du modèle PEER pour mobiliser un grand nombre d’experts. 
Les chercheurs ont également comparé les courbes isoFLOP avec et sans BN. La figure 4 ci-dessous montre que les modèles PEER avec BN peuvent généralement atteindre une perplexité moindre. Bien que la différence ne soit pas significative, elle est plus visible près de la région optimale isoFLOP. 
L'étude PEER n'a qu'un seul auteur, Xu He (Owen), chercheur scientifique chez Google DeepMind et diplômé d'un doctorat de l'Université de Groningen aux Pays-Bas. en 2017. 
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

 Cette approche tente de découpler le coût de calcul du nombre de paramètres en concaténant efficacement un grand nombre de petits experts via une structure d'index apprise pour routage . Démontre une efficacité supérieure par rapport aux couches denses FFW, MoE à gros grains et Product Key Memory (PKM).
Cette approche tente de découpler le coût de calcul du nombre de paramètres en concaténant efficacement un grand nombre de petits experts via une structure d'index apprise pour routage . Démontre une efficacité supérieure par rapport aux couches denses FFW, MoE à gros grains et Product Key Memory (PKM). 
 Enfin, le résultat est calculé en combinant linéairement les résultats des experts pondérés par les scores de routage.
Enfin, le résultat est calculé en combinant linéairement les résultats des experts pondérés par les scores de routage. 

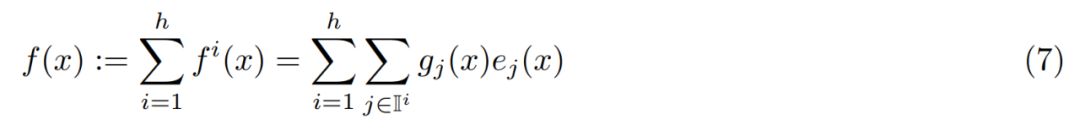






 Comment ouvrir des fichiers HTML
Comment ouvrir des fichiers HTML
 Tutoriel d'installation du système Linux
Tutoriel d'installation du système Linux
 Analyse des perspectives de pièces ICP
Analyse des perspectives de pièces ICP
 Patch VIP Tonnerre
Patch VIP Tonnerre
 Solution de rapport d'erreur de fichier SQL d'importation Mysql
Solution de rapport d'erreur de fichier SQL d'importation Mysql
 Comment résoudre le problème de l'écran noir après avoir allumé l'ordinateur et impossible d'accéder au bureau
Comment résoudre le problème de l'écran noir après avoir allumé l'ordinateur et impossible d'accéder au bureau
 Introduction à l'utilisation de vscode
Introduction à l'utilisation de vscode
 Plateforme de change virtuelle
Plateforme de change virtuelle