Résolvez des calculs financiers complexes avec 3 fonctions financières Excel

Originaltitel: „Diese 3 Excel-Finanzfunktionen werden wieder einmal unterbewertet!“ 》

Der Autor dieses Artikels: Xiaohua

Der Herausgeber dieses Artikels: Yanlan

Kürzlich stieß Xiaohua auf eine interessante Frage, die aus der Seele eines alten Freundes kam:

Wie zahlt man monatliche und private Renten? Treffen Sie eine Wahl für die Finanzierung einer Versicherung auf Gegenseitigkeit?

Die grundlegenden Informationen dieser beiden Finanzprodukte lauten wie folgt:

Monatliche Rente:

Zahlen Sie 1.000 Yuan pro Monat, der jährliche Zinssatz beträgt 3 %, die Laufzeit beträgt 2 Jahre, und der Kapitalbetrag und die Zinsen können betragen bei Fälligkeit auf einmal abgezogen.

Versicherungsfinanzierung auf Gegenseitigkeit:

Zahlen Sie jeden Monat einen Kapitalbetrag von 1.000 Yuan. Der monatliche Kapitalbetrag wird mit 10 % Zinsen und einer Laufzeit von 2 Jahren berechnet. Es nehmen 24 Personen an demselben Produkt teil. Jeden Monat muss eine Person den gesamten Kapitalbetrag und die von den anderen gezahlten Zinsen erhalten. Im nächsten Monat nach Erhalt der Zahlung muss eine Person 100 Yuan pro Monat zahlen.

Wie vergleicht man die Vor- und Nachteile dieser beiden Finanzprodukte?

Wir können dieses Problem anhand der Endwertmethode, der Renditemethode und der IRR-Methode betrachten und nebenbei einige Verwendungen von Finanzfunktionen mit Ihnen teilen.

1. Endwertmethode

Die Methode der Endwertanalyse besteht darin, den Endwert des Nettonutzens des Plans (Projekts) nach Bestimmung des Basisjahres, des Umwandlungszinssatzes und des Cashflows zu berechnen. Je höher der Endwert, desto größer ist die Wirtschaftlichkeit der Lösung.

Wie viel Kapital und Zinsen können nach Fälligkeit der Rente in gleicher Höhe erhalten werden? Dieses Problem kann mit der Endwertfunktion FV berechnet werden.

Renten-Zukunftswertformel:

=-FV(B3/12,C3,A3)

Es ist ersichtlich, dass, wenn jeden Monat eine Rente von 1.000 Yuan gezahlt wird, die Der Zinssatz wird mit 3 % berechnet. Nach 2 Jahren werden insgesamt 24.703 Yuan an Kapital und Zinsen erhalten.

Der Endwert von „Mutual Insurance Finance“ (vorausgesetzt, es erfolgt keine fortlaufende Investition) hängt von der Reihenfolge ab, in der Kapital und Zinsen abgehoben werden. Je später die Auszahlung erfolgt, desto höher ist das Einkommen. Der Endwert wird wie folgt berechnet:

=S2*U2+S2*T2*(V2-1)-S2*T2*(U2-V2)

Aus Sicht der Endwertmethode wenn Sie den Erhalt sicherstellen können. Wenn der Zahlungszeitraum nach 16 Perioden liegt, ist das Einkommen von „Mutual Insurance Finance“ höher als die monatliche Rente. Wenn der Empfangszeitraum früher als 16 Perioden liegt, ist das Einkommen von „Mutual Insurance Finance“ geringer als die monatliche Rente.

Die Terminal-Value-Methode eignet sich für Investitionsvorhaben mit vergleichbarem Investitionsumfang.

2. Renditemethode

Als ich meinem alten Freund diese vorläufige Schlussfolgerung erzählte, fragte er ungläubig:

Warum beträgt der Nominalzinssatz von „Mutual Insurance Finance“ 10 %? /3 des Einkommens der Teilnehmer höher ist als das der monatlichen Rente, die eine Rendite von nur 3 % hat?

Hier geht es um die Berechnung der Rentabilität.

Die Renditemethode ist eine Investitionsentscheidungsmethode, die die durchschnittliche jährliche Nettorendite eines Investitionsprojekts mit den Kapitalkosten der Investition vergleicht, um festzustellen, ob die Investition wünschenswert ist, und dann den Investitionsplan auswählt die höchste Rendite unter den verfügbaren Anlageplänen.

Natürlich entspricht die monatliche Rentenrendite dem Nominalzinssatz, der bei 3 % liegt.

Wie hoch ist also die Rendite für jeden Zahlungszeitraum von „Mutual Insurance Finance“?

Wir können die Funktion RATE zur Berechnung verwenden.

Die Rendite von „Mutual Insurance Finance“ wird wie folgt berechnet:

=RATE(U2-S2,0,W2,0)*12

Aus der Rate von Renditemethode: Obwohl der Nominalzinssatz der „Mutual Insurance Finance“ bis zu 10 % beträgt, kann die Rendite tatsächlich nur dann 3 % erreichen, wenn die Teilnehmer Kapital und Zinsen nach 16 Perioden erhalten. Die Rendite ist niedriger als das Einkommen der monatlichen Rente. Die Rate beträgt 3 %. Es ist ersichtlich, dass die Rendite der „gegenseitigen Versicherungsfinanzierung“ immer noch hoch ist.

Allerdings ist es unfair zu beurteilen, dass die Erträge der „Versicherungsfinanzierung auf Gegenseitigkeit“ nicht so gut sind wie die der monatlichen Rente „Finanzen“ kann einen Kapitalzufluss im Voraus realisieren. Wenn dieser Teil der Mittel wieder für Investitionen verwendet wird, wird die „gegenseitige Versicherungsfinanzierung“ erheblich verbessert.

Im Finanzmanagement wird häufig der Zeitwert verwendet, um diesen Unterschied zu erklären. Der interne Zinsfuß (IRR) und der Nettobarwert (NPV) können zur Messung der dynamischen Rendite einer Investition verwendet werden.

Unten wählen wir NPV, um diese beiden Finanzprodukte zu vergleichen. Die IRR-Vergleichsmethode ist in diesem Fall nicht anwendbar.

3. Nettobarwertmethode

Bevor wir den Nettobarwert berechnen, müssen wir die Cashflows der beiden Produkte in jeder Periode auflisten und dann die NPV-Funktion zur Berechnung verwenden.

Le paiement mensuel pour la rente mensuelle est de 1 000 yuans. Après 24 versements, le principal et les intérêts de 24 703 yuans seront récupérés en une seule fois. Le flux de trésorerie et la VAN sont calculés comme suit :

= VAN (. B3/12,B2:Y2)

Ici, le taux d'intérêt de la rente mensuelle est directement sélectionné comme taux d'actualisation, et sa valeur actuelle nette doit être de 0. Lors du calcul de la valeur actuelle nette de « Mutual Insurance Finance », nous continuons à utiliser ce taux d'actualisation. Si la valeur actuelle nette de cette dernière est supérieure à 0, cela signifie que les revenus de placement de cette dernière sont meilleurs, sinon ils sont moins bons.

« Mutual Insurance Finance » a plusieurs délais de rétractation possibles, donc lors du calcul du TRI de ce produit, nous devons utiliser un tableau de simulation pour y parvenir.

Calcul de la VAN "Mutual Insurance Finance" :

❶ En prenant la période de retrait comme variable, le flux de trésorerie de chaque période calculé en fonction de la variable est répertorié.

Le flux de trésorerie du capital, un nombre positif indique un paiement, et un nombre négatif indique un retrait.

=IF(E$4=$G$2,-$D$2*23,$D$2)

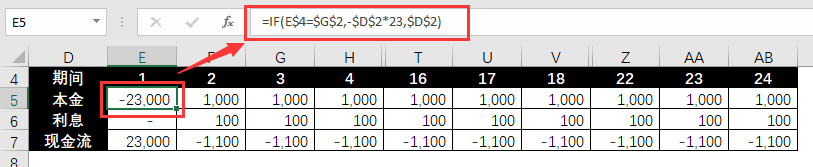
Le flux de trésorerie des intérêts, un nombre positif indique un paiement et un nombre négatif indique une réception.

=IFS(E4$G$2,$D$2*$E$2)

Flux de trésorerie consolidé :

❷ Calculez le TRI sous une seule période de retrait.

=NPV(H2/12,E7:AB7)

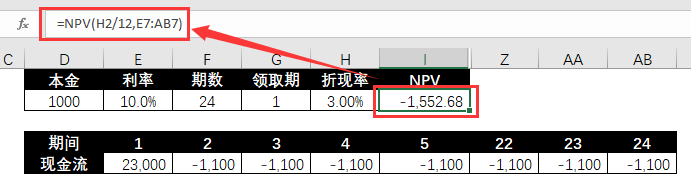
❸ Utilisez le tableau de simulation pour calculer la VAN correspondant aux différentes périodes d'extraction.

① Répertoriez les valeurs des variables de période de collecte requises et liez les valeurs de résultat correspondantes dans la première ligne.

② Sélectionnez la ligne de lien, la zone de valeur variable et la zone de valeur de résultat, et suivez les étapes ci-dessous pour terminer l'opération de simulation.

Les résultats du calcul de simulation sont les suivants :

D'un point de vue VAN, les revenus du « financement d'assurance mutuelle » et de la rente mensuelle sont comparables.

Parmi tous les participants aux premiers, leurs rendements comparatifs sont mitigés. En effet, les participants ayant des périodes de réception plus précoces peuvent obtenir des rentrées de fonds plus rapidement pour un investissement continu, ce qui protège dans une certaine mesure contre la perte de taux d'intérêt élevés.

Pour résumer, lorsqu' il est impossible de réaliser un investissement continu ou de rechercher la certitude, vous devez choisir une rente mensuelle pour l'investissement. Ce produit a un revenu de placement stable et un revenu statique moyen plus élevé.

Si vous recherchez des rendements dynamiques plus élevés ou êtes en mesure de réaliser des investissements secondaires après avoir retiré le capital et les intérêts, vous devez choisir « Financement d'assurance mutuelle » pour la gestion financière. Cette dernière a la possibilité d'obtenir une valeur actuelle nette plus élevée et des rendements statiques.

Ce qui précède est une extension de Xiaohua à partir d'un problème de sélection de produits financiers. Il explique l'utilisation de plusieurs formules et fonctions financières Excel, notamment :

❶ Fonction FV et fonction TAUX

❷ Fonction NPV

❸ Table de simulation

Si vous êtes comptable financier, ou si vous avez un besoin ou un intérêt pour les calculs financiers, ces formules et cas pratiques vous seront utiles.

Xiaohua continuera de partager d'autres cas pratiques de calcul des revenus financiers sur Excel et d'utiliser son expérience pratique pour vous aider à utiliser des formules et des outils, alors restez à l'écoute !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!