 développement back-end
développement back-end
 Tutoriel Python
Tutoriel Python
 timeit.repeat - jouer avec les répétitions pour comprendre les modèles
timeit.repeat - jouer avec les répétitions pour comprendre les modèles
timeit.repeat - jouer avec les répétitions pour comprendre les modèles
1. Le problème
Au cours de votre carrière en génie logiciel, vous pourriez rencontrer un morceau de code qui fonctionne mal et prend beaucoup plus de temps que ce qui est acceptable. Pour aggraver les choses, les performances sont incohérentes et assez variables selon plusieurs exécutions.
À l’heure actuelle, il faut accepter qu’en matière de performances logicielles, il y a beaucoup de non-déterminisme en jeu. Les données peuvent être distribuées dans une fenêtre et suivent parfois une distribution normale. D’autres fois, cela peut être irrégulier sans schéma évident.
2. L'approche
C'est à ce moment-là que l'analyse comparative entre en jeu. Exécuter votre code cinq fois, c'est bien, mais en fin de compte, vous ne disposez que de cinq points de données, avec trop de valeur accordée à chaque point de données. Nous avons besoin d'un nombre beaucoup plus grand de répétitions du même bloc de code pour voir un modèle.
3. La question
Combien de points de données faut-il avoir ? Beaucoup de choses ont été écrites à ce sujet, et l'un des articles que j'ai couverts
Une évaluation rigoureuse des performances nécessite la construction de repères,
exécuté et mesuré plusieurs fois afin de faire face au hasard
variation des délais d'exécution. Les chercheurs devraient fournir des mesures
de variation lors de la communication des résultats.
Kalibera, T. et Jones, R. (2013). Un benchmark rigoureux dans des délais raisonnables. Actes du Symposium international 2013 sur la gestion de la mémoire. https://doi.org/10.1145/2491894.2464160
Lors de la mesure des performances, nous souhaiterons peut-être mesurer l'utilisation du processeur, de la mémoire ou du disque pour obtenir une image plus large des performances. Il est généralement préférable de commencer par quelque chose de simple, comme le temps écoulé, car il est plus facile à visualiser. Une utilisation du processeur à 17 % ne nous dit pas grand-chose. Que devrait-il être ? 20% ou 5 ? L'utilisation du processeur n'est pas l'une des façons naturelles par lesquelles les humains perçoivent les performances.
4. L'expérience
Je vais utiliser la méthode timeit.repeat de python pour répéter un simple bloc d'exécution de code. Le bloc de code multiplie simplement les nombres de 1 à 2000.
from functools import reduce reduce((lambda x, y: x * y), range(1, 2000))
Voici la signature de la méthode
(function) def repeat(
stmt: _Stmt = "pass",
setup: _Stmt = "pass",
timer: _Timer = ...,
repeat: int = 5,
number: int = 1000000,
globals: dict[str, Any] | None = None
) -> list[float]
Que sont la répétition et le numéro ?
Commençons par le nombre. Si le bloc de code est trop petit, il se terminera si rapidement que vous ne pourrez rien mesurer. Cet argument mentionne le nombre de fois que stmt doit être exécuté. Vous pouvez considérer cela comme le nouveau bloc de code. Le float renvoyé correspond au temps d'exécution du numéro stmt X.
Dans notre cas, nous garderons le nombre à 1000 puisque la multiplication jusqu'à 2000 coûte cher.
Ensuite, passez à la répétition. Ceci spécifie le nombre de répétitions ou le nombre de fois que le bloc ci-dessus doit être exécuté. Si la répétition vaut 5, alors la liste[float] renvoie 5 éléments.
Commençons par créer un bloc d'exécution simple
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
Nous voulons l'exécuter dans différentes valeurs de répétition
repeat_values = [5, 20, 100, 500, 3000, 10000]
Le code est assez simple et direct
5. Explorer les résultats
Nous arrivons maintenant à la partie la plus importante de l'expérience : l'interprétation des données. Veuillez noter que différentes personnes peuvent l'interpréter différemment et qu'il n'y a pas une seule bonne réponse.
Votre définition de la bonne réponse dépend beaucoup de ce que vous essayez d'accomplir. Êtes-vous préoccupé par la dégradation des performances de 95 % de vos utilisateurs ? Ou êtes-vous inquiet de la dégradation des performances de la queue de 5 % de vos utilisateurs qui sont assez vocaux ?
5.1. Statistiques d'analyse du temps d'exécution pour plusieurs valeurs de répétition
Comme on peut le constater, les temps min et max sont farfelus. Il montre comment un seul point de données peut suffire à modifier la valeur de la moyenne. Le pire, c'est que High Min et High Max correspondent à des valeurs de répétitions différentes. Il n’y a pas de corrélation et cela montre simplement le pouvoir des valeurs aberrantes.
Ensuite, nous passons à la médiane et remarquons qu'à mesure que nous augmentons le nombre de répétitions, la médiane diminue, sauf 20. Qu'est-ce qui peut l'expliquer ? Cela montre simplement à quel point un plus petit nombre de répétitions implique que nous n'obtenons pas nécessairement l'intégralité des valeurs possibles.
Passons à la moyenne tronquée, où les 2,5 % les plus bas et les 2,5 % les plus élevés sont tronqués. Ceci est utile lorsque vous ne vous souciez pas des utilisateurs aberrants et que vous souhaitez vous concentrer sur les performances des 95 % intermédiaires de vos utilisateurs.
Attention, essayer d'améliorer les performances des 95 % des utilisateurs moyens comporte la possibilité de dégrader les performances des 5 % des utilisateurs aberrants.

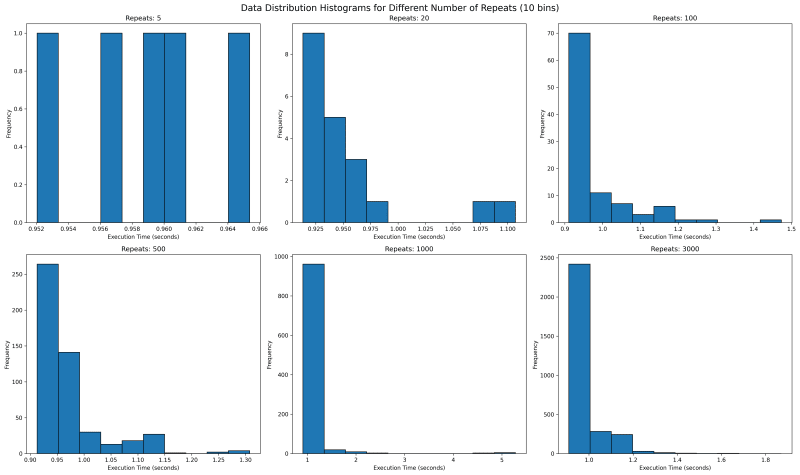
5.2. Execution Time Distribution for multiple values of repeat
Next we want to see where all the data lies. We would use histogram with bin of 10 to see where the data falls. With repetitions of 5 we see that they are mostly equally spaced. This is not one usually expects as sampled data should follow a normal looking distribution.
In our case the value is bounded on the lower side and unbounded on the upper side, since it will take more than 0 seconds to run any code, but there is no upper time limit. This means our distribution should look like a normal distribution with a long right tail.
Going forward with higher values of repeat, we see a tail emerging on the right. I would expect with higher number of repeat, there would be a single histogram bar, which is tall enough that outliers are overshadowed.
5.3. Execution Time Distribution for values 1000 and 3000
How about we look at larger values of repeat to get a sense? We see something unusual. With 1000 repeats, there are a lot of outliers past 1.8 and it looks a lot more tighter. The one on the right with 3000 repeat only goes upto 1.8 and has most of its data clustered around two peaks.
What can it mean? It can mean a lot of things including the fact that sometimes maybe the data gets cached and at times it does not. It can point to many other side effects of your code, which you might have never thought of. With the kind of distribution of both 1000 and 3000 repeats, I feel the TM95 for 3000 repeat is the most accurate value.

6. Appendix
6.1. Code
import timeit
import matplotlib.pyplot as plt
import json
import os
import statistics
import numpy as np
def run_experiment(number_of_repeats, number_of_runs=1000):
execution_time = timeit.repeat(
"from functools import reduce; reduce((lambda x, y: x * y), range(1, 2000))",
repeat=number_of_repeats,
number=number_of_runs
)
return execution_time
def save_result(result, repeats):
filename = f'execution_time_results_{repeats}.json'
with open(filename, 'w') as f:
json.dump(result, f)
def load_result(repeats):
filename = f'execution_time_results_{repeats}.json'
if os.path.exists(filename):
with open(filename, 'r') as f:
return json.load(f)
return None
def truncated_mean(data, percentile=95):
data = np.array(data)
lower_bound = np.percentile(data, (100 - percentile) / 2)
upper_bound = np.percentile(data, 100 - (100 - percentile) / 2)
return np.mean(data[(data >= lower_bound) & (data <= upper_bound)])
# List of number_of_repeats to test
repeat_values = [5, 20, 100, 500, 1000, 3000]
# Run experiments and collect results
results = []
for repeats in repeat_values:
result = load_result(repeats)
if result is None:
print(f"Running experiment for {repeats} repeats...")
try:
result = run_experiment(repeats)
save_result(result, repeats)
print(f"Experiment for {repeats} repeats completed and saved.")
except KeyboardInterrupt:
print(f"\nExperiment for {repeats} repeats interrupted.")
continue
else:
print(f"Loaded existing results for {repeats} repeats.")
# Print time taken per repetition
avg_time = statistics.mean(result)
print(f"Average time per repetition for {repeats} repeats: {avg_time:.6f} seconds")
results.append(result)
trunc_means = [truncated_mean(r) for r in results]
medians = [np.median(r) for r in results]
mins = [np.min(r) for r in results]
maxs = [np.max(r) for r in results]
# Create subplots
fig, axs = plt.subplots(2, 2, figsize=(15, 12))
fig.suptitle('Execution Time Analysis for Different Number of Repeats', fontsize=16)
metrics = [
('Truncated Mean (95%)', trunc_means),
('Median', medians),
('Min', mins),
('Max', maxs)
]
for (title, data), ax in zip(metrics, axs.flatten()):
ax.plot(repeat_values, data, marker='o')
ax.set_title(title)
ax.set_xlabel('Number of Repeats')
ax.set_ylabel('Execution Time (seconds)')
ax.set_xscale('log')
ax.grid(True, which="both", ls="-", alpha=0.2)
# Set x-ticks and labels for each data point
ax.set_xticks(repeat_values)
ax.set_xticklabels(repeat_values)
# Rotate x-axis labels for better readability
ax.tick_params(axis='x', rotation=45)
plt.tight_layout()
# Save the plot to a file
plt.savefig('execution_time_analysis.png', dpi=300, bbox_inches='tight')
print("Plot saved as 'execution_time_analysis.png'")
# Create histograms for data distribution with 10 bins
fig, axs = plt.subplots(2, 3, figsize=(20, 12))
fig.suptitle('Data Distribution Histograms for Different Number of Repeats (10 bins)', fontsize=16)
for repeat, result, ax in zip(repeat_values, results, axs.flatten()):
ax.hist(result, bins=10, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the histograms to a file
plt.savefig('data_distribution_histograms_10bins.png', dpi=300, bbox_inches='tight')
print("Histograms saved as 'data_distribution_histograms_10bins.png'")
# Create histograms for 1000 and 3000 repeats with 30 bins
fig, axs = plt.subplots(1, 2, figsize=(15, 6))
fig.suptitle('Data Distribution Histograms for 1000 and 3000 Repeats (30 bins)', fontsize=16)
for repeat, result, ax in zip([1000, 3000], results[-2:], axs):
ax.hist(result, bins=100, edgecolor='black')
ax.set_title(f'Repeats: {repeat}')
ax.set_xlabel('Execution Time (seconds)')
ax.set_ylabel('Frequency')
plt.tight_layout()
# Save the detailed histograms to a file
plt.savefig('data_distribution_histograms_detailed.png', dpi=300, bbox_inches='tight')
print("Detailed histograms saved as 'data_distribution_histograms_detailed.png'")
plt.show()
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1670
1670
 14
14
 1428
1428
 52
52
 1329
1329
 25
25
 1276
1276
 29
29
 1256
1256
 24
24
 Python vs C: courbes d'apprentissage et facilité d'utilisation
Apr 19, 2025 am 12:20 AM
Python vs C: courbes d'apprentissage et facilité d'utilisation
Apr 19, 2025 am 12:20 AM
Python est plus facile à apprendre et à utiliser, tandis que C est plus puissant mais complexe. 1. La syntaxe Python est concise et adaptée aux débutants. Le typage dynamique et la gestion automatique de la mémoire le rendent facile à utiliser, mais peuvent entraîner des erreurs d'exécution. 2.C fournit des fonctionnalités de contrôle de bas niveau et avancées, adaptées aux applications haute performance, mais a un seuil d'apprentissage élevé et nécessite une gestion manuelle de la mémoire et de la sécurité.
 Python et temps: tirer le meilleur parti de votre temps d'étude
Apr 14, 2025 am 12:02 AM
Python et temps: tirer le meilleur parti de votre temps d'étude
Apr 14, 2025 am 12:02 AM
Pour maximiser l'efficacité de l'apprentissage de Python dans un temps limité, vous pouvez utiliser les modules DateTime, Time et Schedule de Python. 1. Le module DateTime est utilisé pour enregistrer et planifier le temps d'apprentissage. 2. Le module de temps aide à définir l'étude et le temps de repos. 3. Le module de planification organise automatiquement des tâches d'apprentissage hebdomadaires.
 Python vs. C: Explorer les performances et l'efficacité
Apr 18, 2025 am 12:20 AM
Python vs. C: Explorer les performances et l'efficacité
Apr 18, 2025 am 12:20 AM
Python est meilleur que C dans l'efficacité du développement, mais C est plus élevé dans les performances d'exécution. 1. La syntaxe concise de Python et les bibliothèques riches améliorent l'efficacité du développement. Les caractéristiques de type compilation et le contrôle du matériel de CC améliorent les performances d'exécution. Lorsque vous faites un choix, vous devez peser la vitesse de développement et l'efficacité de l'exécution en fonction des besoins du projet.
 Python vs C: Comprendre les principales différences
Apr 21, 2025 am 12:18 AM
Python vs C: Comprendre les principales différences
Apr 21, 2025 am 12:18 AM
Python et C ont chacun leurs propres avantages, et le choix doit être basé sur les exigences du projet. 1) Python convient au développement rapide et au traitement des données en raison de sa syntaxe concise et de son typage dynamique. 2) C convient à des performances élevées et à une programmation système en raison de son typage statique et de sa gestion de la mémoire manuelle.
 Apprendre Python: 2 heures d'étude quotidienne est-elle suffisante?
Apr 18, 2025 am 12:22 AM
Apprendre Python: 2 heures d'étude quotidienne est-elle suffisante?
Apr 18, 2025 am 12:22 AM
Est-ce suffisant pour apprendre Python pendant deux heures par jour? Cela dépend de vos objectifs et de vos méthodes d'apprentissage. 1) Élaborer un plan d'apprentissage clair, 2) Sélectionnez les ressources et méthodes d'apprentissage appropriées, 3) la pratique et l'examen et la consolidation de la pratique pratique et de l'examen et de la consolidation, et vous pouvez progressivement maîtriser les connaissances de base et les fonctions avancées de Python au cours de cette période.
 Quelle partie fait partie de la bibliothèque standard Python: listes ou tableaux?
Apr 27, 2025 am 12:03 AM
Quelle partie fait partie de la bibliothèque standard Python: listes ou tableaux?
Apr 27, 2025 am 12:03 AM
PythonlistSaReparmentofthestandardLibrary, tandis que les coloccules de colocède, tandis que les colocculations pour la base de la Parlementaire, des coloments de forage polyvalent, tandis que la fonctionnalité de la fonctionnalité nettement adressée.
 Python: automatisation, script et gestion des tâches
Apr 16, 2025 am 12:14 AM
Python: automatisation, script et gestion des tâches
Apr 16, 2025 am 12:14 AM
Python excelle dans l'automatisation, les scripts et la gestion des tâches. 1) Automatisation: La sauvegarde du fichier est réalisée via des bibliothèques standard telles que le système d'exploitation et la fermeture. 2) Écriture de script: utilisez la bibliothèque PSUTIL pour surveiller les ressources système. 3) Gestion des tâches: utilisez la bibliothèque de planification pour planifier les tâches. La facilité d'utilisation de Python et la prise en charge de la bibliothèque riche en font l'outil préféré dans ces domaines.
 Python pour le développement Web: applications clés
Apr 18, 2025 am 12:20 AM
Python pour le développement Web: applications clés
Apr 18, 2025 am 12:20 AM
Les applications clés de Python dans le développement Web incluent l'utilisation des cadres Django et Flask, le développement de l'API, l'analyse et la visualisation des données, l'apprentissage automatique et l'IA et l'optimisation des performances. 1. Framework Django et Flask: Django convient au développement rapide d'applications complexes, et Flask convient aux projets petits ou hautement personnalisés. 2. Développement de l'API: Utilisez Flask ou DjangorestFramework pour construire RestulAPI. 3. Analyse et visualisation des données: utilisez Python pour traiter les données et les afficher via l'interface Web. 4. Apprentissage automatique et AI: Python est utilisé pour créer des applications Web intelligentes. 5. Optimisation des performances: optimisée par la programmation, la mise en cache et le code asynchrones



