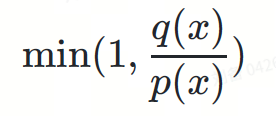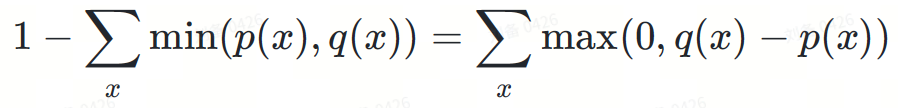Périphériques technologiques
Périphériques technologiques
 IA
IA
 L'échantillonnage spéculatif perdra-t-il la précision d'inférence des grands modèles de langage ?
L'échantillonnage spéculatif perdra-t-il la précision d'inférence des grands modèles de langage ?
L'échantillonnage spéculatif perdra-t-il la précision d'inférence des grands modèles de langage ?
ミッチェル・スターンらは、2018年に投機的サンプリングのプロトタイプコンセプトを提案しました。その後、このアプローチは、Lookahead Decoding、REST、Medusa、EAGLEなどのさまざまな研究によってさらに開発および洗練されており、投機的サンプリングにより大規模言語モデル (LLM) の推論プロセスが大幅に高速化されています。
重要な質問は、LLM の投機的サンプリングは元のモデルの精度を損なうのかということです。答えから始めましょう: いいえ。
標準の投機的サンプリング アルゴリズムはロスレスであり、この記事では数学的分析と実験を通じてこれを証明します。
数学的証明
推測的なサンプリング公式は次のように定義できます:

ここで:
- ? は一様分布からサンプリングされた実数です。
-
 は、次に予測されるトークンです。
は、次に予測されるトークンです。 - ?(?) は、ドラフト モデルによって与えられる次のトークン配布です。
- ?(?) は、基本モデルによって与えられる次のトークン分布です。
簡単にするために、確率条件を省略します。実際、? と ? はプレフィックス トークン シーケンス  に基づいた条件付き分布です。
に基づいた条件付き分布です。
以下は、DeepMind 論文 でのこの式の無損失性の証明です:

数式を読むのが退屈すぎると感じる場合は、次にいくつかの直観的な図を通して証明プロセスを説明します。
これはドラフトモデル ? と基本モデル ? の分布図です:
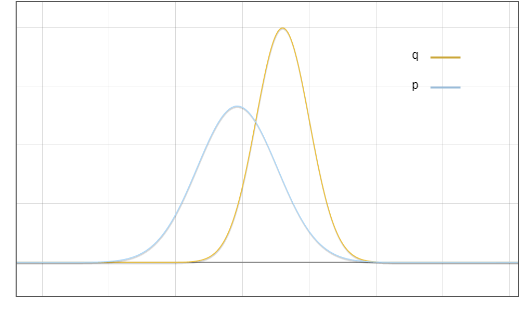
図 1: ドラフトモデル p と基本モデル q の出力分布の確率密度関数
これは単なる理想化されたグラフであることを理解してください。実際に計算するのは、次のような離散分布です。
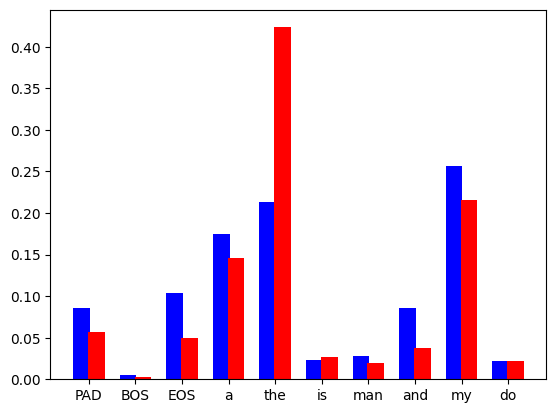
図 2: 言語モデルは、語彙セット内の各トークンの離散確率分布を予測します。青いバーはドラフト モデルからのもので、赤いバーはベースモデルのものです。
ただし、単純化と明確化のために、連続近似を使用してこの問題について説明します。
ここで問題は、分布 ? からサンプリングしますが、最終結果は ? からサンプリングしたものと同じになるようにすることです。重要なアイデアは、赤色の領域の確率を黄色の領域に移動することです:
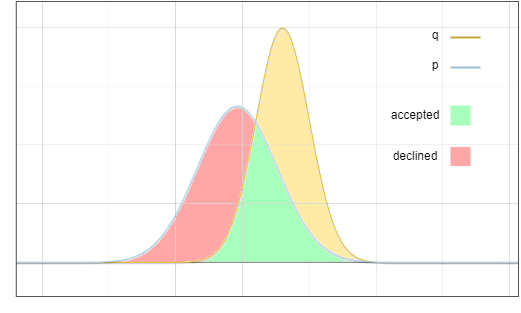
図 3: 合格および拒否のサンプリング領域
ターゲット分布は 2 つの部分の合計として見ることができます:
I。受け入れ
このブランチには 2 つの独立したイベントがあります:
- ドラフト配布でのサンプリング ? は特定のトークンを生成します。確率は ?(?)
- ランダム変数 ? トークンを受け入れます。確率は次のとおりです:

これらの確率を掛け合わせます: 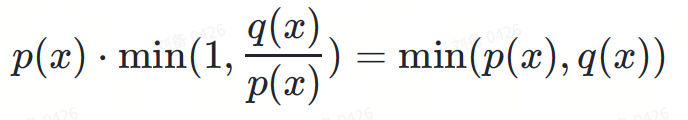
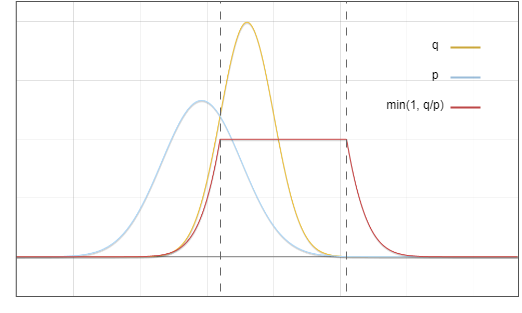
図 4: 青と赤の線を乗算すると、結果は図 6 の緑の線になります
II このブランチには検証拒否
があります。また、2 つの独立したイベント:
- ? は ? で特定のトークンを拒否します。確率は次のとおりです:

これは整数値であり、値は特定のトークン x とは関係ありません。
- は、分布 ?−?(部分的) アップサンプリングにより特定のトークンが生成されます?、確率は次のとおりです:
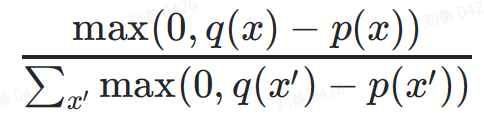
其分母作用是对概率分布进行归一化,以保持概率密度积分等于 1。
两项相乘,第二项的分母被约掉:
max(0,?(?)−?(?))
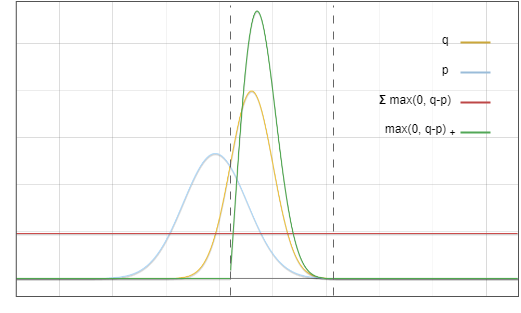
图5. 该图中的红线与绿线对应函数相乘,结果等于图6中的红线
为什么拒绝概率恰好可以归一化max(0,?−?) ?看起来似乎是巧合,这里一个重要的观察是,图 3 中红色区域的面积等于黄色区域的面积,因为所有概率密度函数的积分都等于 1。
将I, II两部分相加: 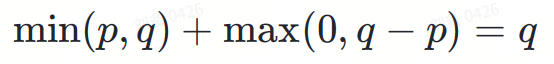
最后,我们得到了目标分布 ?。
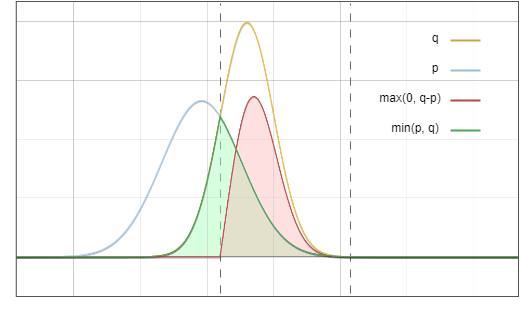
图6. 绿色区域与红色区域相加,正好等于黄线以下的面积
而这正是我们的目标。
实验
尽管我们已经从原理上证明了投机采样是无损的,但算法的实现仍然可能存在bug。因此,实验验证也是必要的。
我们对两种情况进行了实验:贪婪解码的确定性方法和多项式采样的随机方法。
贪婪解码
我们要求 LLM 生成两次短篇故事,首先使用普通推理,然后使用投机采样。两次采样温度均设置为 0。我们使用了 Medusa 中的投机采样实现。模型权重为 medusa-1.0-vicuna-7b-v1.5 及其基础模型 vicuna-7b-v1.5。
测试运行完成后,我们得到了两个精确相同的结果。生成的文本如下:
|
User: Please tell a tale about a cyperpunk knight named PPIO keeps a charming llama as his pet. Assistant: Once upon a time, in a world where technology had advanced beyond our wildest dreams, there lived a cyberpunk knight named PPIO. PPIO was a skilled warrior, with advanced cybernetic enhancements that gave him incredible strength and speed. He was also a man of great honor, always striving to do what was right and just. One day, while out on a mission, PPIO stumbled upon a beautiful llama. Despite being a cybernetic being, PPIO had a soft spot for animals and he couldn't resist rescuing the llama from whatever danger it may have been in. From that day on, the llama followed PPIO wherever he went, and the two became fast friends. The llama, whose name was Llama-ella, was a special llama. It had a unique ability to sense when someone was in danger and would let out a loud, distinctive call to alert them to the danger. PPIO was grateful for Llama-ella's ability and the two became an unstoppable team. Together, PPIO and Llama-ella took on all sorts of challenges, from battling cybernetic villains to rescuing innocent people from harm. They were a force to be reckoned with, and their bravery and honor were an inspiration to all who knew them. |
多项式采样
在随机采样的情况下,情况更加复杂。大多数在随机程序中重现结果的方法都使用固定的随机种子来利用伪随机生成器的确定性。但是,这种方法不适合我们的场景。我们的实验依赖于大数定律:如果有足够的样本,则实际分布与理论分布之间的误差将收敛于零。
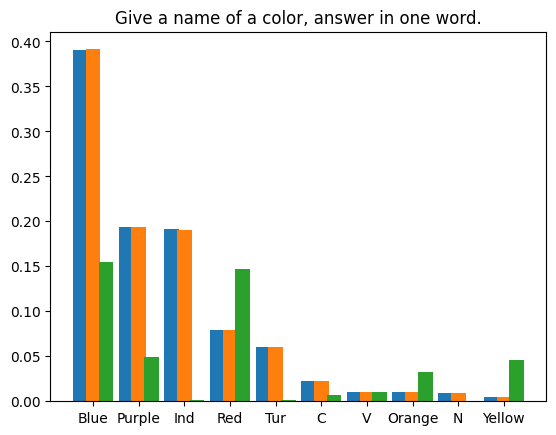
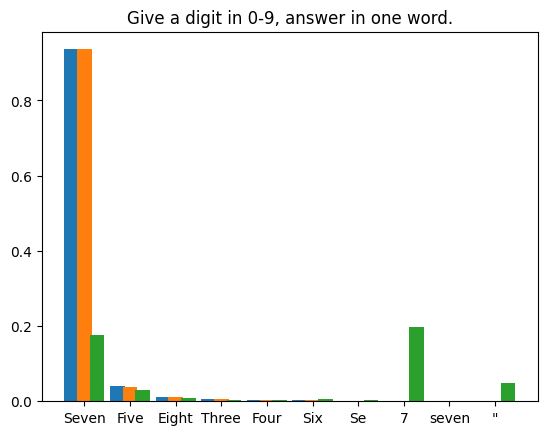
我们编制了四个提示文本,对LLM在每个提示下生成的首个token进行了 1,000,000 次投机采样迭代。使用的模型权重为 Llama3 8B Instruct 和 EAGLE-LLaMA3-Instruct-8B。统计结果如下所示:
|
|
|
|
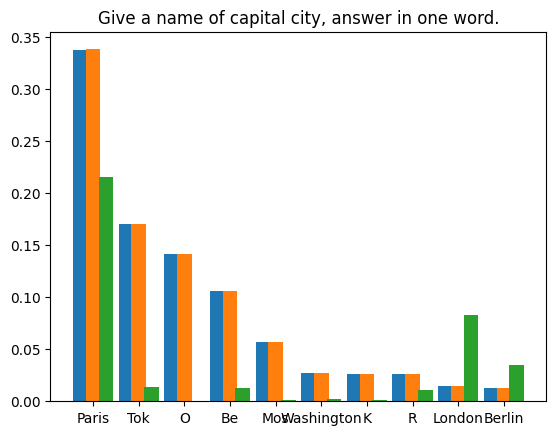
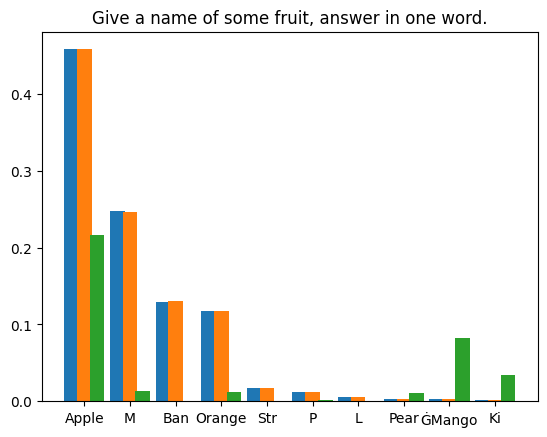
- Vert : softmax à partir des logits de sortie du modèle de baseOrange : à partir de la fonte Échantillonnage de la machine (1 000 000 de fois) Le premier proportion de comptage de
- L'écart type entre le résultat de sortie du modèle de base et la distribution d'échantillonnage est de 9,694e-5. Comme prévu.
L'échantillonnage spéculatif ne nuit pas à la précision de l'inférence des grands modèles de langage. Grâce à une analyse mathématique rigoureuse et à des expériences pratiques, nous démontrons la nature sans perte de l'algorithme d'échantillonnage spéculatif standard. La preuve mathématique montre comment la formule d'échantillonnage spéculatif préserve la distribution originale du modèle sous-jacent. Nos expériences, notamment le décodage glouton déterministe et l'échantillonnage polynomial probabiliste, valident davantage ces résultats théoriques. L'expérience de décodage glouton a produit les mêmes résultats avec et sans échantillonnage spéculatif, tandis que l'expérience d'échantillonnage polynomial a montré que la différence dans la distribution des jetons est négligeable sur un grand nombre d'échantillons. Ensemble, ces résultats démontrent que l'échantillonnage spéculatif peut accélérer considérablement l'inférence LLM sans sacrifier la précision, ouvrant la voie à des systèmes d'IA plus efficaces et plus accessibles à l'avenir.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1667
1667
 14
14
 1426
1426
 52
52
 1328
1328
 25
25
 1273
1273
 29
29
 1255
1255
 24
24
 L'auteur de ControlNet a encore un succès ! L'ensemble du processus de génération d'une peinture à partir d'une image, gagnant 1,4k étoiles en deux jours
Jul 17, 2024 am 01:56 AM
L'auteur de ControlNet a encore un succès ! L'ensemble du processus de génération d'une peinture à partir d'une image, gagnant 1,4k étoiles en deux jours
Jul 17, 2024 am 01:56 AM
Il s'agit également d'une vidéo Tusheng, mais PaintsUndo a emprunté une voie différente. L'auteur de ControlNet, LvminZhang, a recommencé à vivre ! Cette fois, je vise le domaine de la peinture. Le nouveau projet PaintsUndo a reçu 1,4kstar (toujours en hausse folle) peu de temps après son lancement. Adresse du projet : https://github.com/lllyasviel/Paints-UNDO Grâce à ce projet, l'utilisateur saisit une image statique et PaintsUndo peut automatiquement vous aider à générer une vidéo de l'ensemble du processus de peinture, du brouillon de ligne au suivi du produit fini. . Pendant le processus de dessin, les changements de lignes sont étonnants. Le résultat vidéo final est très similaire à l’image originale : jetons un coup d’œil à un dessin complet.
 Du RLHF au DPO en passant par TDPO, les algorithmes d'alignement des grands modèles sont déjà « au niveau des jetons »
Jun 24, 2024 pm 03:04 PM
Du RLHF au DPO en passant par TDPO, les algorithmes d'alignement des grands modèles sont déjà « au niveau des jetons »
Jun 24, 2024 pm 03:04 PM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com Dans le processus de développement de l'intelligence artificielle, le contrôle et le guidage des grands modèles de langage (LLM) ont toujours été l'un des principaux défis, visant à garantir que ces modèles sont à la fois puissant et sûr au service de la société humaine. Les premiers efforts se sont concentrés sur les méthodes d’apprentissage par renforcement par feedback humain (RL
 En tête de liste des ingénieurs logiciels d'IA open source, la solution sans agent de l'UIUC résout facilement les problèmes de programmation réels du banc SWE.
Jul 17, 2024 pm 10:02 PM
En tête de liste des ingénieurs logiciels d'IA open source, la solution sans agent de l'UIUC résout facilement les problèmes de programmation réels du banc SWE.
Jul 17, 2024 pm 10:02 PM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com Les auteurs de cet article font tous partie de l'équipe de l'enseignant Zhang Lingming de l'Université de l'Illinois à Urbana-Champaign (UIUC), notamment : Steven Code repair ; doctorant en quatrième année, chercheur
 Les articles arXiv peuvent être publiés sous forme de 'barrage', la plateforme de discussion alphaXiv de Stanford est en ligne, LeCun l'aime
Aug 01, 2024 pm 05:18 PM
Les articles arXiv peuvent être publiés sous forme de 'barrage', la plateforme de discussion alphaXiv de Stanford est en ligne, LeCun l'aime
Aug 01, 2024 pm 05:18 PM
acclamations! Qu’est-ce que ça fait lorsqu’une discussion sur papier se résume à des mots ? Récemment, des étudiants de l'Université de Stanford ont créé alphaXiv, un forum de discussion ouvert pour les articles arXiv qui permet de publier des questions et des commentaires directement sur n'importe quel article arXiv. Lien du site Web : https://alphaxiv.org/ En fait, il n'est pas nécessaire de visiter spécifiquement ce site Web. Il suffit de remplacer arXiv dans n'importe quelle URL par alphaXiv pour ouvrir directement l'article correspondant sur le forum alphaXiv : vous pouvez localiser avec précision les paragraphes dans. l'article, Phrase : dans la zone de discussion sur la droite, les utilisateurs peuvent poser des questions à l'auteur sur les idées et les détails de l'article. Par exemple, ils peuvent également commenter le contenu de l'article, tels que : "Donné à".
 Une avancée significative dans l'hypothèse de Riemann ! Tao Zhexuan recommande fortement les nouveaux articles du MIT et d'Oxford, et le lauréat de la médaille Fields, âgé de 37 ans, a participé
Aug 05, 2024 pm 03:32 PM
Une avancée significative dans l'hypothèse de Riemann ! Tao Zhexuan recommande fortement les nouveaux articles du MIT et d'Oxford, et le lauréat de la médaille Fields, âgé de 37 ans, a participé
Aug 05, 2024 pm 03:32 PM
Récemment, l’hypothèse de Riemann, connue comme l’un des sept problèmes majeurs du millénaire, a réalisé une nouvelle avancée. L'hypothèse de Riemann est un problème mathématique non résolu très important, lié aux propriétés précises de la distribution des nombres premiers (les nombres premiers sont les nombres qui ne sont divisibles que par 1 et par eux-mêmes, et jouent un rôle fondamental dans la théorie des nombres). Dans la littérature mathématique actuelle, il existe plus d'un millier de propositions mathématiques basées sur l'établissement de l'hypothèse de Riemann (ou sa forme généralisée). En d’autres termes, une fois que l’hypothèse de Riemann et sa forme généralisée seront prouvées, ces plus d’un millier de propositions seront établies sous forme de théorèmes, qui auront un impact profond sur le domaine des mathématiques et si l’hypothèse de Riemann s’avère fausse, alors parmi eux ; ces propositions qui en font partie perdront également de leur efficacité. Une nouvelle percée vient du professeur de mathématiques du MIT, Larry Guth, et de l'Université d'Oxford
 Travail posthume de l'équipe OpenAI Super Alignment : deux grands modèles jouent à un jeu et le résultat devient plus compréhensible
Jul 19, 2024 am 01:29 AM
Travail posthume de l'équipe OpenAI Super Alignment : deux grands modèles jouent à un jeu et le résultat devient plus compréhensible
Jul 19, 2024 am 01:29 AM
Si la réponse donnée par le modèle d’IA est incompréhensible du tout, oseriez-vous l’utiliser ? À mesure que les systèmes d’apprentissage automatique sont utilisés dans des domaines de plus en plus importants, il devient de plus en plus important de démontrer pourquoi nous pouvons faire confiance à leurs résultats, et quand ne pas leur faire confiance. Une façon possible de gagner confiance dans le résultat d'un système complexe est d'exiger que le système produise une interprétation de son résultat qui soit lisible par un humain ou un autre système de confiance, c'est-à-dire entièrement compréhensible au point que toute erreur possible puisse être trouvé. Par exemple, pour renforcer la confiance dans le système judiciaire, nous exigeons que les tribunaux fournissent des avis écrits clairs et lisibles qui expliquent et soutiennent leurs décisions. Pour les grands modèles de langage, nous pouvons également adopter une approche similaire. Cependant, lorsque vous adoptez cette approche, assurez-vous que le modèle de langage génère
 LLM n'est vraiment pas bon pour la prédiction de séries chronologiques. Il n'utilise même pas sa capacité de raisonnement.
Jul 15, 2024 pm 03:59 PM
LLM n'est vraiment pas bon pour la prédiction de séries chronologiques. Il n'utilise même pas sa capacité de raisonnement.
Jul 15, 2024 pm 03:59 PM
Les modèles linguistiques peuvent-ils vraiment être utilisés pour la prédiction de séries chronologiques ? Selon la loi des gros titres de Betteridge (tout titre d'actualité se terminant par un point d'interrogation peut recevoir une réponse « non »), la réponse devrait être non. Le fait semble être vrai : un LLM aussi puissant ne peut pas bien gérer les données de séries chronologiques. Les séries chronologiques, c'est-à-dire les séries chronologiques, comme leur nom l'indique, font référence à un ensemble de séquences de points de données disposées par ordre temporel. L'analyse des séries chronologiques est essentielle dans de nombreux domaines, notamment la prévision de la propagation des maladies, l'analyse du commerce de détail, la santé et la finance. Dans le domaine de l'analyse des séries chronologiques, de nombreux chercheurs ont récemment étudié comment utiliser les grands modèles linguistiques (LLM) pour classer, prédire et détecter les anomalies dans les séries chronologiques. Ces articles supposent que les modèles de langage capables de gérer les dépendances séquentielles dans le texte peuvent également se généraliser aux séries chronologiques.
 Le premier MLLM basé sur Mamba est là ! Les poids des modèles, le code de formation, etc. sont tous open source
Jul 17, 2024 am 02:46 AM
Le premier MLLM basé sur Mamba est là ! Les poids des modèles, le code de formation, etc. sont tous open source
Jul 17, 2024 am 02:46 AM
La colonne AIxiv est une colonne où ce site publie du contenu académique et technique. Au cours des dernières années, la rubrique AIxiv de ce site a reçu plus de 2 000 rapports, couvrant les meilleurs laboratoires des principales universités et entreprises du monde entier, favorisant efficacement les échanges et la diffusion académiques. Si vous souhaitez partager un excellent travail, n'hésitez pas à contribuer ou à nous contacter pour un rapport. Courriel de soumission : liyazhou@jiqizhixin.com ; zhaoyunfeng@jiqizhixin.com. Introduction Ces dernières années, l'application de grands modèles de langage multimodaux (MLLM) dans divers domaines a connu un succès remarquable. Cependant, en tant que modèle de base pour de nombreuses tâches en aval, le MLLM actuel se compose du célèbre réseau Transformer, qui



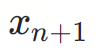 は、次に予測されるトークンです。
は、次に予測されるトークンです。