Étude de cas : le problème des cercles connectés

Le problème des cercles connectés consiste à déterminer si tous les cercles dans un plan bidimensionnel sont connectés. Ce problème peut être résolu en utilisant un parcours en profondeur d'abord. L'algorithme DFS a de nombreuses applications. Cette section applique l'algorithme DFS pour résoudre le problème des cercles connectés.

Dans le problème des cercles connectés, vous déterminez si tous les cercles d'un plan bidimensionnel sont connectés. Si tous les cercles sont connectés, ils sont peints comme des cercles pleins, comme le montre la figure ci-dessous (a). Sinon, ils ne sont pas remplis, comme le montre la figure ci-dessous (b).

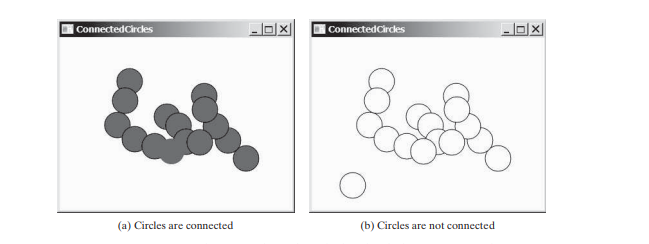
Nous allons écrire un programme qui permet à l'utilisateur de créer un cercle en cliquant avec la souris dans une zone vide qui n'est actuellement pas couverte par un cercle. Au fur et à mesure que les cercles sont ajoutés, les cercles sont repeints remplis s'ils sont connectés ou vides sinon.

Nous allons créer un graphique pour modéliser le problème. Chaque cercle est un sommet du graphique. Deux cercles sont connectés s'ils se chevauchent. Nous appliquons le DFS dans le graphique, et si tous les sommets sont trouvés dans la recherche en profondeur d'abord, le graphique est connecté.

Le programme est donné dans le code ci-dessous.

import javafx.application.Application;
import javafx.geometry.Point2D;
import javafx.scene.Node;
import javafx.scene.Scene;
import javafx.scene.layout.Pane;
import javafx.scene.paint.Color;
import javafx.scene.shape.Circle;
import javafx.stage.Stage;

public class ConnectedCircles extends Application {
    @Override // Override the start method in the Application class
    public void start(Stage primaryStage) {
        // Create a scene and place it in the stage
        Scene scene = new Scene(new CirclePane(), 450, 350);
        primaryStage.setTitle("ConnectedCircles"); // Set the stage title
        primaryStage.setScene(scene); // Place the scene in the stage
        primaryStage.show(); // Display the stage
    }

    public static void main(String[] args) {
        Application.launch(args);
    }

    /** Pane for displaying circles */
    class CirclePane extends Pane {
        public CirclePane() {
            this.setOnMouseClicked(e -> {
                if (!isInsideACircle(new Point2D(e.getX(), e.getY()))) {
                    // Add a new circle
                    getChildren().add(new Circle(e.getX(), e.getY(), 20));
                    colorIfConnected();
                }
            });
        }

        /** Returns true if the point is inside an existing circle */
        private boolean isInsideACircle(Point2D p) {
            for (Node circle: this.getChildren())
                if (circle.contains(p))
                    return true;

            return false;
        }

        /** Color all circles if they are connected */
        private void colorIfConnected() {
            if (getChildren().size() == 0)
                return; // No circles in the pane

            // Build the edges
            java.util.List<AbstractGraph.Edge> edges = new java.util.ArrayList<>();
            for (int i = 0; i < getChildren().size(); i++)
                for (int j = i + 1; j < getChildren().size(); j++)
                    if (overlaps((Circle)(getChildren().get(i)), (Circle)(getChildren().get(j)))) {
                        edges.add(new AbstractGraph.Edge(i, j));
                        edges.add(new AbstractGraph.Edge(j, i));
                    }

            // Create a graph with circles as vertices
            Graph<Node> graph = new UnweightedGraph<>((java.util.List<Node>)getChildren(), edges);
            AbstractGraph<Node>.Tree tree = graph.dfs(0); // a DFS tree
            boolean isAllCirclesConnected = getChildren().size() == tree.getNumberOfVerticesFound();

            for (Node circle: getChildren()) {
                if (isAllCirclesConnected) { // All circles are connected
                    ((Circle)circle).setFill(Color.RED);
                }
                else {
                    ((Circle)circle).setStroke(Color.BLACK);
                    ((Circle)circle).setFill(Color.WHITE);
                }
            }
        }
    }

    public static boolean overlaps(Circle circle1, Circle circle2) {
        return new Point2D(circle1.getCenterX(), circle1.getCenterY()).distance(circle2.getCenterX(), circle2.getCenterY()) <= circle1.getRadius() + circle2.getRadius();
    }
}

La classe JavaFX Circle contient les champs de données x, y et rayon, qui spécifient l'emplacement central et le rayon du cercle. . Il définit également le contient pour tester si un point est dans le cercle. La méthode chevauchements (lignes 76 à 80) vérifie si deux cercles se chevauchent.

Lorsque l'utilisateur clique avec la souris en dehors de tout cercle existant, un nouveau cercle est créé centré au point de la souris et le cercle est ajouté au volet (ligne 26).

Pour détecter si les cercles sont connectés, le programme construit un graphique (lignes 46 à 59). Les cercles sont les sommets du graphique. Les bords sont construits selon les lignes 49 à 55. Deux sommets de cercle sont connectés s'ils se chevauchent (ligne 51). La DFS du graphique donne un arbre (ligne 60). Le getNumberOfVerticesFound() de l'arbre renvoie le nombre de sommets recherchés. S'il est égal au nombre de cercles, tous les cercles sont connectés (lignes 61-62).

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!