Jusqu'où pouvez-vous optimiser un programme pour calculer la séquence de Fibonacci ?

Jusqu’où pouvez-vous optimiser un programme pour calculer la séquence de Fibonacci ?

Introduction

Quand j'apprenais Python, notre professeur nous a donné un devoir : calculer le Nième nombre de la séquence de Fibonacci.

Je pense que c'est très simple, alors j'écris ce code :

def fib(n):
    if n == 0:
        return 0
    elif n == 1:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

Plus tard, je sais que ce genre de solution coûte trop de temps.

Optimiser un programme

Je change la solution en itération.

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1]+ls[i-2])

    return ls[n-1]

J'utilise matplotlib draw le temps que ça coûte :

import time
import matplotlib.pyplot as plt


def bench_mark(func, *args):
    # calculate the time
    start = time.perf_counter()
    result = func(*args)
    end = time.perf_counter()

    return end - start, result  # return the time and the result

def fib(n):
    ls = [1,1]
    for i in range(2,n):
        ls.append(ls[i-1]+ls[i-2])

    return ls[n-1]

mark_list = []

for i in range(1,10000):
    mark = bench_mark(fib,i)
    mark_list.append(mark[0])
    print(f"size : {i} , time : {mark[0]}")

plt.plot(range(1, 10000), mark_list)
plt.xlabel('Input Size')
plt.ylabel('Execution Time (seconds)')
plt.title('Test fot fibonacci')
plt.grid(True)
plt.show()

Résultat ici :

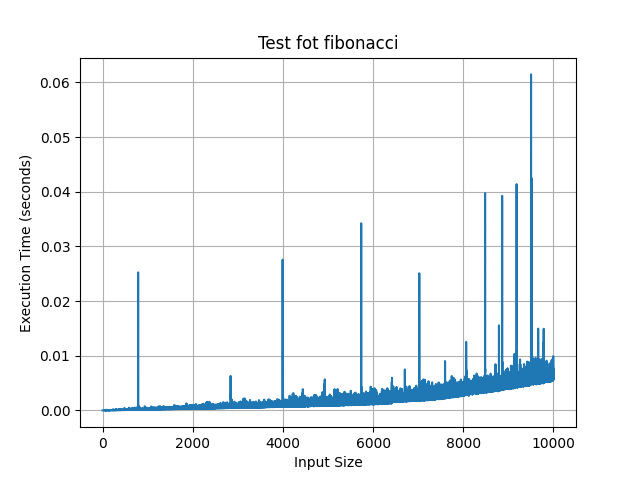
Le temps que cela coûte est très court.

Mais j'écris fib(300000), cela coûte 5,719049899998936 secondes. C'est trop long.

Quand je serai grand, j'apprends CACHE, donc je change de solution pour utiliser dict pour stocker le résultat.

from functools import lru_cache
@lru_cache(maxsize=None)
def fib(n):
    if n < 2:
        return 1
    else:
        return fib(n - 1) + fib(n - 2)

Ou nous pouvons écrire le CACHE par nous-mêmes.

def fib(n, cache={}):
    if n in cache:
        return cache[n]
    elif n < 2:
        return 1
    else:
        ls = [1, 1]
        for i in range(2, n):
            next_value = ls[-1] + ls[-2]
            ls.append(next_value)
            cache[i] = next_value
        cache[n-1] = ls[-1]
        return ls[-1]

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!