Programme Java pour supprimer les doublons d'une pile donnée

Dans cet article, nous explorerons deux méthodes pour supprimer les éléments en double d'une pile en Java. Nous comparerons une approche simple avec des boucles imbriquées et une méthode plus efficace utilisant un HashSet. L'objectif est de démontrer comment optimiser la suppression des doublons et d'évaluer les performances de chaque approche.

Énoncé du problème

Écrivez un programme Java pour supprimer l'élément en double de la pile.

Entrée

Stack<Integer> data = initData(10L);

Sortie

Unique elements using Naive Approach: [1, 4, 3, 2, 8, 7, 5]
Time spent for Naive Approach: 18200 nanoseconds

Unique elements using Optimized Approach: [1, 4, 3, 2, 8, 7, 5]
Time spent for Optimized Approach: 34800 nanoseconds

Pour supprimer les doublons d'une pile donnée, nous avons 2 approches −

• Approche naïve : créez deux boucles imbriquées pour voir quels éléments sont déjà présents et éviter de les ajouter au retour de la pile de résultats.
• Approche HashSet : utilisez un Set pour stocker des éléments uniques et profitez de sa complexité O(1) pour vérifier si un élément est présent ou non.

Génération et clonage de piles aléatoires

Ci-dessous, le programme Java construit d'abord une pile aléatoire, puis en crée une copie pour une utilisation ultérieure −

private static Stack initData(Long size) {
    Stack stack = new Stack < > ();
    Random random = new Random();
    int bound = (int) Math.ceil(size * 0.75);
    for (int i = 0; i < size; ++i) {
        stack.add(random.nextInt(bound) + 1);
    }
    return stack;
}

private static Stack < Integer > manualCloneStack(Stack < Integer > stack) {
    Stack < Integer > newStack = new Stack < > ();
    for (Integer item: stack) {
        newStack.push(item);
    }
    return newStack;
}

initData aide à créer une pile avec une taille spécifiée et des éléments aléatoires allant de 1 à 100.

manualCloneStack aide à générer des données en copiant les données d'une autre pile, en les utilisant pour comparer les performances entre les deux idées.

Supprimez les doublons d'une pile donnée en utilisant l'approche Naïve

Voici l'étape pour supprimer les doublons d'une pile donnée en utilisant l'approche Naïve −

• Démarrez le chronomètre.
• Créez une pile vide pour stocker des éléments uniques.
• Itérez en utilisant la boucle while et continuez jusqu'à ce que la pile d'origine soit vide, faites apparaître l'élément supérieur.
• Recherchez les doublons à l'aide de resultStack.contains(element) pour voir si l'élément est déjà dans la pile de résultats.
• Si l'élément n'est pas dans la pile de résultats, ajoutez-le à resultStack.
• Enregistrez l'heure de fin et calculez le temps total passé.
• Résultat de retour

Exemple

Vous trouverez ci-dessous le programme Java permettant de supprimer les doublons d'une pile donnée en utilisant l'approche Naïve −

public static Stack idea1(Stack stack) {
  long start = System.nanoTime();
  Stack resultStack = new Stack < > ();

  while (!stack.isEmpty()) {
    int element = stack.pop();
    if (!resultStack.contains(element)) {
      resultStack.add(element);
    }
  }
  System.out.println("Time spent for idea1 is %d nanosecond".formatted(System.nanoTime() - start));
  return resultStack;
}

Pour l'approche Naive, nous utilisons

<code>while (!stack.isEmpty())</code>

pour gérer la première boucle pour parcourir tous les éléments de la pile, et la deuxième boucle est <div class="code" style="position:relative; padding:0px; margin:0px;"><pre class="brush:php;toolbar:false">resultStack.contains(element)</pre><div class="contentsignin">Copier après la connexion</div></div> pour vérifier si l'élément est déjà présent.

Supprimez les doublons d'une pile donnée en utilisant une approche optimisée (HashSet)

Voici l'étape pour supprimer les doublons d'une pile donnée en utilisant une approche optimisée −

• Démarrez le chronomètre
• Créez un ensemble pour suivre les éléments vus (pour les contrôles de complexité O(1)).
• Créez une pile temporaire pour stocker des éléments uniques.
• Itérez en utilisant la boucle while continuez jusqu'à ce que la pile soit vide.
• Supprimez l'élément supérieur de la pile.
• Pour vérifier les doublons, nous utiliserons seen.contains(element) pour vérifier si l'élément est déjà dans l'ensemble.
• Si l'élément n'est pas dans l'ensemble, ajoutez-le à la fois à la pile vue et à la pile temporaire.
• Enregistrez l'heure de fin et calculez le temps total passé.
• Renvoie le résultat

Exemple

Vous trouverez ci-dessous le programme Java permettant de supprimer les doublons d'une pile donnée à l'aide de HashSet −

public static Stack<Integer> idea2(Stack<Integer> stack) {
    long start = System.nanoTime();
    Set<Integer> seen = new HashSet<>();
    Stack<Integer> tempStack = new Stack<>();

    while (!stack.isEmpty()) {
        int element = stack.pop();
        if (!seen.contains(element)) {
            seen.add(element);
            tempStack.push(element);
        }
    }
    System.out.println("Time spent for idea2 is %d nanosecond".formatted(System.nanoTime() - start));
    return tempStack;
}

Pour une approche optimisée, nous utilisons

<code>Set<Integer> seen</code>

pour stocker des éléments uniques dans un Set, profitez de la O(1) complexité lors de l'accès à un élément aléatoire pour réduire le coût de calcul pour vérifier si un élément est présent ou non.

Utiliser les deux approches ensemble

Vous trouverez ci-dessous l'étape pour supprimer les doublons d'une pile donnée en utilisant les deux approches mentionnées ci-dessus -

• Initialisez les données, nous utilisons la méthode initData (Long size) pour créer une pile remplie d'entiers aléatoires.
  
• Clonez la pile, nous utilisons la méthode cloneStack (Stack stack) pour créer une copie exacte de la pile d'origine.
• Générez la pile initiale avec initData.
• Clonez cette pile en utilisant cloneStack.
• Appliquez l' approche naïve pour supprimer les doublons de la pile d'origine.
• Appliquez l'approche optimisée pour supprimer les doublons de la pile clonée.
• Affichez le temps nécessaire pour chaque méthode et les éléments uniques produits par les deux approches

Exemple 

Vous trouverez ci-dessous le programme Java qui supprime les éléments en double d'une pile en utilisant les deux approches mentionnées ci-dessus −

import java.util.HashSet;
import java.util.Random;
import java.util.Set;
import java.util.Stack;

public class DuplicateStackElements {
    private static Stack<Integer> initData(Long size) {
        Stack<Integer> stack = new Stack<>();
        Random random = new Random();
        int bound = (int) Math.ceil(size * 0.75);
        for (int i = 0; i < size; ++i) {
            stack.add(random.nextInt(bound) + 1);
        }
        return stack;
    }
    private static Stack<Integer> cloneStack(Stack<Integer> stack) {
        Stack<Integer> newStack = new Stack<>();
        newStack.addAll(stack);
        return newStack;
    }
    public static Stack<Integer> idea1(Stack<Integer> stack) {
        long start = System.nanoTime();
        Stack<Integer> resultStack = new Stack<>();

        while (!stack.isEmpty()) {
            int element = stack.pop();
            if (!resultStack.contains(element)) {
                resultStack.add(element);
            }
        }
        System.out.printf("Time spent for idea1 is %d nanoseconds%n", System.nanoTime() - start);
        return resultStack;
    }
    public static Stack<Integer> idea2(Stack<Integer> stack) {
        long start = System.nanoTime();
        Set<Integer> seen = new HashSet<>();
        Stack<Integer> tempStack = new Stack<>();

        while (!stack.isEmpty()) {
            int element = stack.pop();
            if (!seen.contains(element)) {
                seen.add(element);
                tempStack.push(element);
            }
        }
        System.out.printf("Time spent for idea2 is %d nanoseconds%n", System.nanoTime() - start);
        return tempStack;
    }
    public static void main(String[] args) {
        Stack<Integer> data1 = initData(10L);
        Stack<Integer> data2 = cloneStack(data1);
        System.out.println("Unique elements using idea1: " + idea1(data1));
        System.out.println("Unique elements using idea2: " + idea2(data2));
    }
}

Sortie

Comparaison

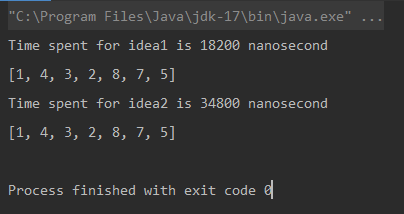
* L'unité de mesure est la nanoseconde.

public static void main(String[] args) {
    Stack<Integer> data1 = initData(<number of stack size want to test>);
    Stack<Integer> data2 = manualCloneStack(data1);
    idea1(data1);
    idea2(data2);
}

Method	100 elements	1000 elements	10000 elements	100000 elements	1000000 elements
Idea 1	693100	4051600	19026900	114201800	1157256000
Idea 2	135800	681400	2717800	11489400	36456100

As observed, the time running for Idea 2 is shorter than for Idea 1 because the complexity of Idea 1 is O(n²), while the complexity of Idea 2 is O(n). So, when the number of stacks increases, the time spent on calculations also increases based on it.

---

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!