
L'arbre AVL est également connu comme un arbre binaire auto-équilibré qui est utilisé pour équilibrer et calculer la différence entre les hauteurs respectives des sous-arbres gauche et droit dont le résultat ne peut pas être supérieur à un dans l'ensemble de l'arbre équilibré. L’opération de l’arborescence de recherche binaire permet les opérations d’insertion, de suppression, de recherche, max et min qui sont également nécessaires dans le cadre de l’arborescence AVL. Toutes ces opérations sont considérées comme des affaires coûteuses, de sorte que si la différence entre les hauteurs de tous les BST est maintenue, la complexité en termes de coût et de temps qui y est associée peut être maintenue.
Commencez votre cours de développement de logiciels libres
Développement Web, langages de programmation, tests de logiciels et autres
Syntaxe :
Il n'existe pas de syntaxe appropriée en tant que telle, mais lors de son implémentation dans Java, l'arborescence AVL est considérée comme une structure de données où la syntaxe est représentée comme suit :
Class Node_demo
{
int key, height_0;
Node left, right;
Node_demo (int d_1)
{
key = d_1;
height_0 = 1;
}
}
class AVLTree_demo1 {
Node root_0;
int height_0(Node N_1) {
if (N_1== null)
return 0;
return N_1.height;
}Explication :
Dans le flux de syntaxe ici, la classe Node_demo contient la clé, la hauteur et la structure qui décrivent la paire clé-valeur où les éléments seront stockés. Suivi du nœud AVL_Tree demo_1 contenant le nœud racine et ses éléments associés avec des paires de valeurs ayant une hauteur à maintenir partout avec des valeurs nulles.
Où D représente ce nœud dont la hauteur et le facteur d'équilibre sont différents de -1, 1 et 0, raison pour laquelle toutes ces rotations sont nécessaires pour les rendre correctement au format.
Il existe de nombreuses opérations qui existent et pour cela, il faut avoir des rotations appropriées avec une analyse appropriée pour la manipulation.
Exemple : Cet exemple montre l'arborescence AVL où l'insertion, l'insertion gauche et droite avec une représentation de précommande, de postcommande et d'ordre de niveau, comme indiqué dans la sortie ci-dessous.
import java. util.LinkedList;
import java.util.Queue;
class Node_8 {
int data_0, height_1;
Node_8 left_nd_0;
Node_8 right_nd_0;
Node_8(int d_2) {
data_0 = d_2;
height_1 = 1;
}
}
public class AVLTree_Demo
{
Node_8 root_0;
int height_1(Node_8 N) {
if (N == null)
return 0;
return N.height_1;
}
int max_2(int a_0, int b_0) {
return (a_0 > b_0) ? a_0 : b_0;
}
Node_8 rightRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.left_nd_0;
Node_8 temp_0 = newRoot_0.right_nd_0;
newRoot_0.right_nd_0 = oldRoot_0;
oldRoot_0.left_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1 = max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
Node_8 leftRotation_mode(Node_8 oldRoot_0) {
Node_8 newRoot_0 = oldRoot_0.right_nd_0;
Node_8 temp_0 = newRoot_0.left_nd_0;
newRoot_0.left_nd_0 = oldRoot_0;
oldRoot_0.right_nd_0 = temp_0;
newRoot_0.height_1 = max_2(height_1(newRoot_0.left_nd_0), height_1(newRoot_0.right_nd_0)) + 1;
oldRoot_0.height_1=max_2(height_1(oldRoot_0.left_nd_0), height_1(oldRoot_0.right_nd_0)) + 1;
return newRoot_0;
}
int balFactor_c(Node_8 root_0) {
if(root_0 == null)
return 0;
return height_1(root_0.left_nd_0) - height_1(root_0.right_nd_0);
}
Node_8 insert(Node_8 root_0, int data_0) {
if(root_0 == null)
return new Node_8(data_0);
else if(data_0 < root_0.data_0)
root_0.left_nd_0 = insert(root_0.left_nd_0, data_0);
else if(data_0 > root_0.data_0)
root_0.right_nd_0 = insert(root_0.right_nd_0, data_0);
else
return root_0;
root_0.height_1= max_2(height_1(root_0.left_nd_0), height_1(root_0.right_nd_0)) + 1;
int bal = balFactor_c(root_0);
if(bal > 1 && data_0 < root_0.left_nd_0.data_0)
return rightRotation_mode(root_0);
if(bal < -1 && data_0 > root_0.right_nd_0.data_0)
return leftRotation_mode(root_0);
if(bal > 1 && data_0 > root_0.left_nd_0.data_0) {
root_0.left_nd_0 = leftRotation_mode(root_0.left_nd_0);
return rightRotation_mode(root_0);
}
if(bal < -1 && data_0 < root_0.right_nd_0.data_0) {
root_0.right_nd_0 = rightRotation_mode(root_0.right_nd_0);
return leftRotation_mode(root_0);
}
return root_0;
}
void preOrder_traversal(Node_8 node) {
if (node != null) {
System.out.print(node.data_0 + " ");
preOrder_traversal(node.left_nd_0);
preOrder_traversal(node.right_nd_0);
}
}
void levelOrder_traversal(Node_8 root) {
Queue<Node_8> q_1 = new LinkedList<Node_8>();
q_1.add(root);
while(!q_1.isEmpty()) {
Node_8 current = q_1.peek();
System.out.print(current.data_0 + " ");
if(current.left_nd_0 != null)
q_1.add(current.left_nd_0);
if(current.right_nd_0 != null)
q_1.add(current.right_nd_0);
q_1.poll();
}
}
public static void main (String args[]) {
AVLTree_Demo tree = new AVLTree_Demo ();
tree. root_0 = tree.insert(tree.root_0, 15);
tree.root_0 = tree.insert(tree.root_0, 20);
tree.root_0 = tree.insert(tree.root_0, 19);
tree.root_0 = tree.insert(tree.root_0, 40);
tree.root_0 = tree.insert(tree.root_0, 50);
tree.root_0 = tree.insert(tree.root_0, 25);
System.out.println("order_of_Preorder_traversal_representation : ");
tree.preOrder_traversal(tree.root_0);
System.out.println();
System.out.println("Levelorder_of_traversal_representation : ");
tree.levelOrder_traversal(tree.root_0);
}
}Sortie :
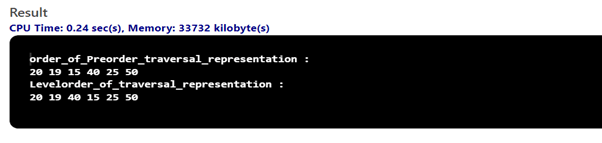
Explication : Ce programme effectue l'insertion d'éléments dans l'arbre AVL post dont il y a un certain ordre de manière à ce que certains vérifient comme si la liste prise est vide ou non et ensuite si l'arbre AVL a rotations à effectuer dans un format de pré-commande, de post-commande ou d'ordre de niveau. Tous les éléments donnés prennent automatiquement en compte les entrées et les organisent dans le bon ordre.
L'arborescence AVL en Java est utilisée comme une structure de données appropriée qui est appréciée par de nombreux développeurs car elle donne un avantage en termes d'opérations et aide à économiser et à consommer la complexité du temps créée par un grand ensemble de codes. L'arborescence AVL a la capacité de gérer des opérations majeures telles que l'insertion, la suppression, la rotation et la suppression de l'ensemble des sous-arbres si les hauteurs sont correctement maintenues.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!