
Un arbre de recherche binaire est une structure de données qui nous permet de conserver une liste triée de nombres en peu de temps. On l'appelle également arbre binaire car chaque nœud d'arbre ne peut avoir que deux frères et sœurs. L'arbre de recherche binaire peut être utilisé pour rechercher la présence d'un nombre ; c'est ce qu'on appelle un arbre de recherche. La complexité du temps d'exécution est le temps O(log(n)) ; les caractéristiques qui distinguent un arbre de recherche binaire d'un arbre binaire de base sont les suivantes –
Commencez votre cours de développement de logiciels libres
Développement Web, langages de programmation, tests de logiciels et autres
1. Les nœuds du sous-arbre gauche sont tous plus petits que le nœud racine.
2. Les nœuds du sous-arbre droit sont tous supérieurs au nœud racine.
3. Chaque nœud des sous-arbres est également un BST, ce qui signifie qu'ils ont les deux mêmes qualités que le nœud lui-même.
1. Soit le tableau spécifié :
Tableau donné : [8, 6, 2, 7, 9, 12, 4, 10]
2. Commençons par l’élément supérieur 43. Insérez 43 comme racine de l’arbre.
3. Si l'élément suivant est inférieur à l'élément du nœud racine, il doit être inséré comme racine du sous-arbre gauche.
4. Sinon, il doit être inséré comme racine du sous-arbre de droite.
L'image ci-dessous décrit le processus de construction d'un arbre de recherche binaire à l'aide des éléments fournis.
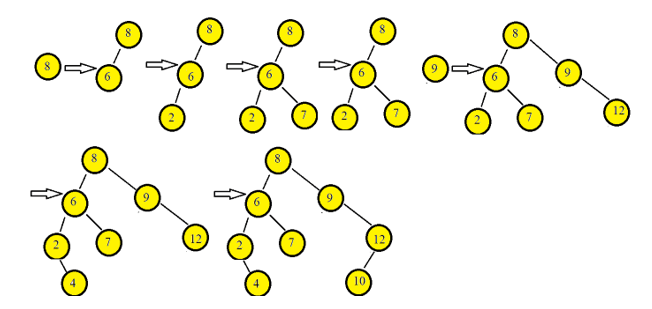
Opérations sur l'arbre de recherche binaire :
Les opérations prises en charge par l'arbre de recherche binaire en Java sont affichées dans la liste ci-dessous –
1. Recherche dans BST – Dans un arbre de recherche binaire, trouver la position d'un certain élément.
2. Insertion dans BST – L'ajout d'un nouvel élément à l'arbre de recherche binaire au bon emplacement garantit que la propriété de l'arbre de recherche binaire n'est pas rompue.
3. Suppression dans BST – Supprimez un nœud spécifique dans un arbre de recherche binaire. Cependant, en fonction du nombre d'enfants d'un nœud, il peut exister divers scénarios de suppression.
Exemple d'arbre de recherche binaire en Java pour effectuer une opération sur l'arbre de recherche binaire –
// Le programme peut être testé dans Eclipse IDE, JAVA 11
package jex;
import java.util.Scanner;
class binarySearchTree {
//node class that defines BST node
class Node {
int key;
Node left, right;
public Node(int data){
key = data;
left = right = null;
}
}
// binary search tree root node
Node root;
// Constructor for binary search tree, first empty tree
binarySearchTree(){
root = null;
}
//delete a node from binary search tree
void deleteKey(int key) {
root = delete(root, key);
}
//recursive delete function
Node delete(Node root, int key) {
// if tree is empty
if (root == null) return root;
//traverse the tree
if (key < root.key)
//traverse left subtree
root.left = delete(root.left, key);
else if (key > root.key)
//traverse right subtree
root.right = delete(root.right, key);
else {
// if node having only one child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
// if node has two children;
root.key = minKey(root.right);
// removing the inorder sibling
root.right = delete(root.right, root.key);
}
return root;
}
int minKey(Node root) {
// initially min is root
int min = root.key;
// find minimum value
while (root.left != null) {
min = root.left.key;
root = root.left;
}
return min;
}
// insert a node in binary search tree
void insertKey(int key) {
root = insert(root, key);
}
// recursively insert a node
Node insert(Node root, int key) {
// initially, tree is empty
if (root == null) {
root = new Node(key);
return root;
}
// traverse the tree
if (key<root.key)
//insert in the left subtree
root.left = insert(root.left, key);
else if (key > root.key)
//insert in the right subtree
root.right = insert(root.right, key);
// return
return root;
}
// function to travel inorder of binary search tree
void inorder() {
inorder(root);
}
// recursively traverse the binary search tree
void inorder(Node root) {
if (root != null) {
inorder(root.left);
System.out.print(root.key + " ");
inorder(root.right);
}
}
boolean searchKey(int key) {
root = search(root, key);
if (root!= null)
return true;
else
return false;
}
//recursive insert function
Node search(Node root, int key) {
// If root is null or key is present at root
if (root==null || root.key==key)
return root;
// when val is greater than root's key
if (root.key > key)
return search(root.left, key);
// when val is lesser than root's key
return search(root.right, key);
}
}
public class client{
public static void main(String[] args) {
binarySearchTree t = new binarySearchTree();
// inserting 8, 6, 2, 7, 9, 12, 4, 10 data into the binary search tree
t.insertKey(8);
t.insertKey(6);
t.insertKey(2);
t.insertKey(7);
t.insertKey(9);
t.insertKey(12);
t.insertKey(4);
t.insertKey(10);
//print the binary search tree
System.out.println( "The binary search tree created with the input data :");
t.inorder();
//delete the leaf node
System.out.println( "\nThe binary search tree after deleting 4 leaf node :");
t.deleteKey(4);
t.inorder();
//delete the node with one child
System.out.println( "\nThe binary search tree after Delete 12 node with 1 child is :");
t.deleteKey(12);
t.inorder();
//search a key in the binary search tree
boolean res = t.searchKey (9);
System.out.println( "\n The node 9 found in binary search tree is :" + res );
res = t.searchKey (12);
System.out.println( "\n The node 10 found in binary search tree is :" + res );
}
}Sortie :
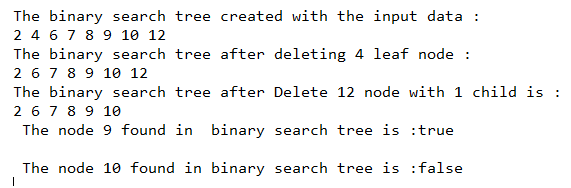
Comme dans le programme ci-dessus, la classe binaireSearchTree est créée, qui contient une autre classe interne Node et contient également le constructeur et les méthodes. Les méthodes définies dans la classe sont deleteKey(), delete(), minKey(), insertKey(), insert(), inorder(), searchKey() et search() pour effectuer les opérations spécifiques. Dans la fonction principale, l'objet de classe binaireSearchTree est créé, insérez-y quelques éléments et appelez ensuite les méthodes de la classe binaire Search Tree sur son objet, comme le montre la sortie ci-dessus.
L'arbre de recherche binaire est également connu sous le nom d'arbre binaire car chaque nœud d'arbre ne peut avoir que deux frères et sœurs. Un arbre de recherche binaire est une structure de données qui permet de conserver une liste triée de nombres en peu de temps. L'opération qui peut être effectuée sur l'arbre de recherche binaire : parcours, insertion, suppression et recherche.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!