
Les matrices en Java sont stockées dans des tableaux. Il existe des tableaux unidimensionnels et des tableaux bidimensionnels qui stockent les valeurs sous forme de matrices dans les dimensions appelées tableaux. Il n'y a que des nombres stockés à une dimension dans un tableau à une dimension, tandis que dans les tableaux à deux dimensions, les nombres sont stockés sous forme de lignes et de colonnes. Les matrices peuvent être utilisées pour additionner, soustraire et multiplier des nombres dans le langage de programmation Java. La multiplication matricielle est l'une des tâches les plus compliquées de la méthodologie de programmation Java. Nous devons effectuer une multiplication matricielle en Java dans cet article et montrer comment multiplier deux matrices et fournir un résultat raisonnable.
Commencez votre cours de développement de logiciels libres
Développement Web, langages de programmation, tests de logiciels et autres
La multiplication matricielle dans le langage de programmation Java s'effectue de manière très simple. Tout d’abord, nous saisissons les nombres dans le premier tableau bidimensionnel, puis nous saisissons les numéros des éléments dans le deuxième tableau bidimensionnel. Les nombres sont ajoutés par ligne, ce qui signifie que la première ligne est créée, puis les nombres de la deuxième ligne sont créés et ainsi de suite. Ensuite, la deuxième matrice est créée de la même manière, puis nous commençons à multiplier les nombres dans les matrices.
Vous trouverez ci-dessous les exemples de multiplication matricielle
Dans l'exemple de codage, nous voyons comment deux matrices sont saisies par ligne, puis la multiplication matricielle est effectuée. Le code pour la multiplication de deux matrices est présenté ci-dessous. Trois tableaux sont déclarés. Le produit des première et deuxième matrices est affiché à l’intérieur de la troisième matrice. Ensuite, la matrice est affichée comme une sortie qui est un produit de deux matrices du tableau.
Code :
import java.util.Scanner;
public class MatixMultiplication
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise. \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
b[i][j] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
System.out.print(c[i][j] + " ");
}
System.out.println();
}
input.close();
}
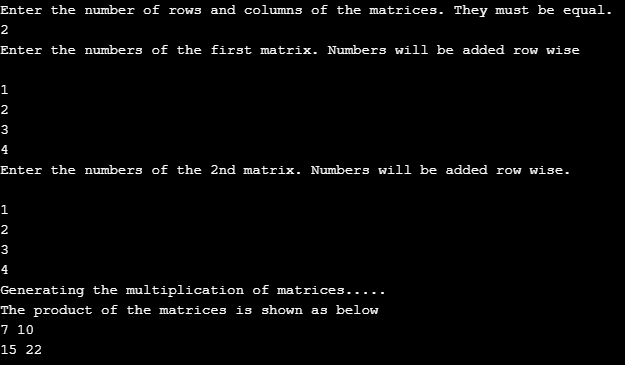
}La sortie d'une matrice 2*2 est affichée. La première matrice est constituée d'éléments comme { 1,2
3,4}
et la deuxième matrice contient également les mêmes éléments. Dans l’exemple de sortie, nous remarquons la multiplication des matrices et l’exemple de sortie. Les éléments de la matrice sont réalisés de façon très soignée. Le résultat produit
{1,2 { 1,2 { 7, 10
3,4} * 3,4} = 15, 22}
Sortie :
Dans l'exemple de codage 2, nous avons le même programme, mais maintenant nous utilisons des tableaux tridimensionnels pour la multiplication. Nous utilisons maintenant la multiplication matricielle 3 * 3 et affichons le résultat dans un autre tableau tridimensionnel.
Code :
import java.util.Scanner;
public class Matix
{
public static void main(String args[])
{
int n;
Scanner input = new Scanner(System.in);
System.out.println("Enter the number of rows and columns of the matrices. They must be equal.");
n = input.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int[][] c = new int[n][n];
System.out.println("Enter the numbers of the first matrix. Numbers will be added row wise \n");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
a[i][j] = input.nextInt();
}
}
System.out.println("Enter the numbers of the 2nd matrix. Numbers will be added row wise. \n");
for (int z = 0; z < n; z++)
{
for (int k = 0; k < n; k++)
{
b[z][k] = input.nextInt();
}
}
System.out.println("Generating the multiplication of matrices.....");
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
for (int k = 0; k < n; k++)
{
c[i][j] = c[i][j] + a[i][k] * b[k][j];
}
}
}
System.out.println("The product of the matrices is shown as below");
for (int k = 0; k < n; k++)
{
for (int l = 0; l < n; l++)
{
System.out.print(c[k][l] + " ");
}
System.out.println();
}
input.close();
}
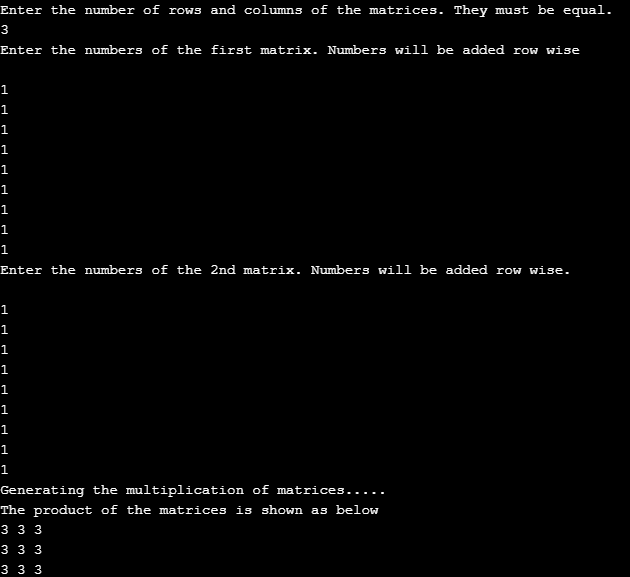
}À partir du deuxième exemple de code, nous imprimons deux matrices 3*3. La première matrice est {1,1,1
1,1,1
1,1,1}
et la deuxième matrice est également la même. La multiplication matricielle est générée des manières suivantes
{1,1,1 {1,1,1 { 3,3,3
1,1,1 * 1,1,1 = 3,3,3
1,1,1} 1,1,1} 3,3,3}
Sortie :
Dans cet article, nous voyons la multiplication d'une matrice 2*2 et d'une matrice 3*3 et le résultat est affiché d'une très belle façon. Les résultats sont clairement donnés. En utilisant la multiplication matricielle, nous pouvons également créer une multiplication 4*4 d’une matrice. La base est demandée lors de la première étape du programme. Nous pouvons également créer des matrices 5*5, 6*6. Plus la base est grande, plus le programme est complexe.
Cependant, la simple multiplication de matrices est très utile pour calculer la réflexion d'un point avec l'axe X, l'axe Y ou l'axe Z comme axe de réflexion. Ces concepts simples sont utilisés en géométrie de coordonnées et sont utilisés dans la modélisation mathématique des applications géométriques.
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!