L'utilité déraisonnable de numpy's einsum

Introduction

J'aimerais vous présenter la méthode la plus utile en Python, np.einsum.

Avec np.einsum (et ses homologues dans Tensorflow et JAX), vous pouvez écrire des opérations matricielles et tensorielles complexes d'une manière extrêmement claire et succincte. J'ai également constaté que sa clarté et sa concision soulagent une grande partie de la surcharge mentale liée au travail avec les tenseurs.

Et c'est en fait assez simple à apprendre et à utiliser. Voici comment cela fonctionne :

Dans np.einsum, vous avez un argument de chaîne d'indices et vous avez un ou plusieurs opérandes :

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

L'argument des indices est un "mini-langage" qui indique à numpy comment manipuler et combiner les axes des opérandes. C'est un peu difficile à lire au début, mais ce n'est pas mal quand on a pris le coup.

Opérandes simples

Pour un premier exemple, utilisons np.einsum pour échanger les axes (c'est-à-dire prendre la transposition) d'une matrice A :

M = np.einsum('ij->ji', A)

Les lettres i et j sont liées aux premier et deuxième axes de A. Numpy lie les lettres aux axes dans l'ordre dans lequel elles apparaissent, mais numpy ne se soucie pas des lettres que vous utilisez si vous êtes explicite. On aurait pu utiliser a et b par exemple, et ça marche de la même manière :

M = np.einsum('ab->ba', A)

Cependant, vous devez fournir autant de lettres qu'il y a d'axes dans l'opérande. Il y a deux axes dans A, vous devez donc fournir deux lettres distinctes. L'exemple suivant ne fonctionnera pas car la formule des indices n'a qu'une seule lettre à lier, i :

# broken
M = np.einsum('i->i', A)

D'un autre côté, si l'opérande n'a effectivement qu'un seul axe (i.o.w., c'est un vecteur), alors la formule d'indice à une seule lettre fonctionne très bien, même si elle n'est pas très utile car elle laisse le vecteur un tel quel :

m = np.einsum('i->i', a)

Résumer sur les axes

Mais qu'en est-il de cette opération ? Il n'y a pas de i à droite. Est-ce valide ?

c = np.einsum('i->', a)

Étonnamment, oui !

Voici la première clé pour comprendre l'essence de np.einsum : si un axe est omis du côté droit, alors l'axe est additionné.

Code :

c = 0
I = len(a)
for i in range(I):
   c += a[i]

Le comportement de sommation ne se limite pas à un seul axe. Par exemple, vous pouvez additionner deux axes à la fois en utilisant cette formule d'indice : c = np.einsum('ij->', A):

Voici le code Python correspondant pour quelque chose sur les deux axes :

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

Mais cela ne s'arrête pas là : nous pouvons faire preuve de créativité et additionner certains axes et en laisser d'autres tranquilles. Par exemple : np.einsum('ij->i', A) additionne les lignes de la matrice A, laissant un vecteur de sommes de lignes de longueur j :

Code :

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

De même, np.einsum('ij->j', A) additionne les colonnes de A.

Code :

M = np.einsum('ij->ji', A)

Deux opérandes

Il y a une limite à ce que nous pouvons faire avec un seul opérande. Les choses deviennent beaucoup plus intéressantes (et utiles) avec deux opérandes.

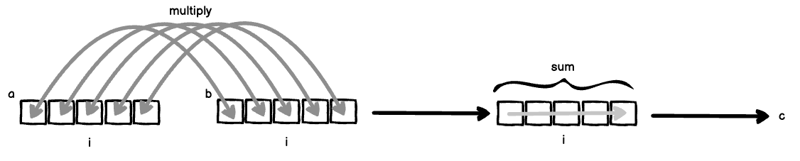
Supposons que vous ayez deux vecteurs a = [a_1, a_2, ... ] et b = [a_1, a_2, ...].

Si len(a) === len(b), nous pouvons calculer le produit scalaire (également appelé produit scalaire) comme ceci :

M = np.einsum('ab->ba', A)

Deux choses se produisent ici simultanément :

1. Parce que i est lié à la fois à a et b, a et b sont "alignés" puis multipliés ensemble : a[i] * b[i].
2. Parce que l'index i est exclu du côté droit, l'axe i est additionné afin de l'éliminer.

Si vous mettez (1) et (2) ensemble, vous obtenez le produit intérieur classique.

Code :

# broken
M = np.einsum('i->i', A)

Maintenant, supposons que nous n'ayons pas omis i de la formule d'indice, nous multiplierions tous les a[i] et b[i] et pas la somme sur i :

m = np.einsum('i->i', a)

Code :

c = np.einsum('i->', a)

Cela est également appelé multiplication par éléments (ou produit Hadamard pour les matrices), et se fait généralement via la méthode numpy np.multiply.

Il existe encore une troisième variante de la formule d'indice, appelée produit externe.

c = 0
I = len(a)
for i in range(I):
   c += a[i]

Dans cette formule d'indice, les axes de a et b sont liés à des lettres séparées et sont donc traités comme des « variables de boucle » distinctes. Par conséquent, C a des entrées a[i] * b[j] pour tous i et j, disposées dans une matrice.

Code :

c = 0
I,J = A.shape
for i in range(I):
   for j in range(J):
      c += A[i,j]

Trois opérandes

En poussant le produit extérieur un peu plus loin, voici une version à trois opérandes :

I,J = A.shape
r = np.zeros(I)
for i in range(I):
   for j in range(J):
      r[i] += A[i,j]

Le code Python équivalent pour notre produit externe à trois opérandes est :

I,J = A.shape
r = np.zeros(J)
for i in range(I):
   for j in range(J):
      r[j] += A[i,j]

En allant encore plus loin, rien ne nous empêche de omettre les axes pour les additionner en plus de transposer le résultat en écrivant ki au lieu de ik à droite de -> :

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Le code Python équivalent serait :

M = np.einsum('ij->ji', A)

Maintenant, j'espère que vous pourrez commencer à voir comment spécifier assez facilement des opérations tensorielles compliquées. Lorsque j'ai travaillé plus intensivement avec numpy, je me suis retrouvé à utiliser np.einsum chaque fois que je devais implémenter une opération tensorielle compliquée.

D'après mon expérience, np.einsum facilite la lecture du code plus tard - je peux facilement lire l'opération ci-dessus directement à partir des indices : "Le produit externe de trois vecteurs, avec les axes médians additionnés et le résultat final transposé ". Si je devais lire une série compliquée d'opérations numpy, je pourrais me retrouver la langue liée.

Un exemple pratique

Pour un exemple pratique, implémentons l'équation au cœur des LLM, tirée de l'article classique "L'attention est tout ce dont vous avez besoin".

Éq. 1 décrit le mécanisme d'attention :

Nous concentrerons notre attention sur le terme $Q{K}^T$QKT , car softmax n'est pas calculable par np.einsum et le facteur d'échelle $\frac{1}{\sqrt{d_k}}$dk​​1 ​ est trivial à appliquer.

Le $Q{K}^T$QKT Le terme représente les produits scalaires de m requêtes avec n clés. Q est une collection de m vecteurs de ligne à d dimensions empilés dans une matrice, donc Q a la forme md. De même, K est une collection de n vecteurs lignes à dimensions d empilés dans une matrice, donc K a la forme md.

Le produit entre un seul Q et K s'écrirait comme suit :

np.einsum('md,nd->mn', Q, K)

Notez qu'en raison de la façon dont nous avons écrit notre équation d'indices, nous avons évité d'avoir à transposer K avant la multiplication matricielle !

Donc, cela semble assez simple – en fait, c'est juste une multiplication matricielle traditionnelle. Cependant, nous n’avons pas encore terminé. L'attention est tout ce dont vous avez besoin utilise l'attention multi-têtes, ce qui signifie que nous avons vraiment k de telles multiplications matricielles se produisant simultanément sur une collection indexée de matrices Q et de matrices K .

Pour rendre les choses un peu plus claires, nous pourrions réécrire le produit comme $Q_i{K}_i^T$Qi​K iT​ .

Cela signifie que nous avons un axe i supplémentaire pour Q et K.

Et de plus, si nous sommes dans un cadre de formation, nous exécutons probablement un lot de telles opérations d'attention multi-têtes.

Je voudrais donc probablement effectuer l'opération sur un lot d'exemples le long d'un axe de lot b. Ainsi, le produit complet ressemblerait à :

numpy.einsum(subscripts : string, *operands : List[np.ndarray])

Je vais sauter le schéma ici car nous avons affaire à des tenseurs à 4 axes. Mais vous pourrez peut-être imaginer « empiler » le diagramme précédent pour obtenir notre axe multi-têtes i, puis « empiler » ces « piles » pour obtenir notre axe de lot b.

Il m'est difficile de voir comment nous implémenterions une telle opération avec n'importe quelle combinaison des autres méthodes numpy. Pourtant, avec un peu d'inspection, ce qui se passe est clair : Sur un lot, sur une collection de matrices Q et K, effectuez la multiplication matricielle Qt(K).

Maintenant, n'est-ce pas merveilleux ?

Prise sans vergogne

Après avoir fait le mode fondateur pendant un an, je recherche du travail. J'ai plus de 15 ans d'expérience dans une grande variété de domaines techniques et de langages de programmation ainsi qu'une expérience en gestion d'équipes. Les mathématiques et les statistiques sont des domaines d'intérêt. Envoyez-moi un message privé et parlons-en !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!