Enquête sur les performances de np.einsum

Un lecteur de mon dernier article de blog m'a fait remarquer que pour les opérations de type matmul par tranche, np.einsum est considérablement plus lent que np.matmul à moins que vous n'activiez l'indicateur d'optimisation dans la liste des paramètres : np.einsum(.. ., optimiser = Vrai).

Étant quelque peu sceptique, j'ai lancé un notebook Jupyter et effectué quelques tests préliminaires. Et je serai damné, c'est tout à fait vrai - même pour les cas à deux opérandes où l'optimisation ne devrait faire aucune différence !

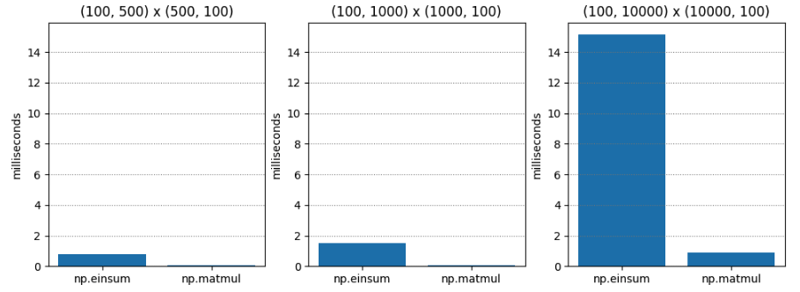
Le test 1 est assez simple : multiplication matricielle de deux matrices d'ordre C (alias ordre majeur de ligne) de dimensions variables. np.matmul est systématiquement environ vingt fois plus rapide.

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.765	0.045	17.055
(100, 1000)	(1000, 100)	1.495	0.073	20.554
(100, 10000)	(10000, 100)	15.148	0.896	16.899

Pour le Test 2, avec optimise=True, les résultats sont radicalement différents. np.einsum est toujours plus lent, mais au pire seulement environ 1,5 fois plus lent !

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.063	0.043	1.474
(100, 1000)	(1000, 100)	0.086	0.067	1.284
(100, 10000)	(10000, 100)	1.000	0.936	1.068

Pourquoi?

Ma compréhension de l'indicateur d'optimisation est qu'il détermine un ordre de contraction optimal lorsqu'il y a trois opérandes ou plus. Ici, nous n'avons que deux opérandes. Donc optimiser ne devrait pas faire de différence, n'est-ce pas ?

Mais peut-être qu'optimiser fait quelque chose de plus que simplement choisir un ordre de contraction ? Peut-être que l'optimisation est consciente de la disposition de la mémoire, et cela a quelque chose à voir avec la disposition des lignes principales et des colonnes principales ?

Dans la méthode de multiplication matricielle de l'école primaire, pour calculer une seule entrée, vous parcourez une ligne dans op1 pendant que vous parcourez une colonne dans op2, donc mettre le deuxième argument dans l'ordre majeur des colonnes peut entraîner une accélération pour np.einsum (en supposant que np.einsum soit un peu comme une version généralisée de la méthode de multiplication matricielle de l'école primaire sous le capot, ce que je soupçonne être vrai).

Donc, pour le Test 3, j'ai passé une matrice de colonne majeure pour le deuxième opérande pour voir si cela accélérait np.einsum lorsque optimise=False.

Voici les résultats. Étonnamment, np.einsum est encore considérablement pire. De toute évidence, il se passe quelque chose que je ne comprends pas - peut-être que np.einsum utilise un chemin de code totalement différent lorsque l'optimisation est True ? Il est temps de commencer à creuser.

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	1.486	0.056	26.541
(100, 1000)	(1000, 100)	3.885	0.125	31.070
(100, 10000)	(10000, 100)	49.669	1.047	47.444

Aller plus loin

Les notes de version de Numpy 1.12.0 mentionnent l'introduction du drapeau d'optimisation. Cependant, le but de l'optimisation semble être de déterminer l'ordre dans lequel les arguments d'une chaîne d'opérandes sont combinés (c'est-à-dire l'associativité) - donc l'optimisation ne devrait pas faire de différence pour seulement deux opérandes, n'est-ce pas ? Voici les notes de version :

np.einsum prend désormais en charge l'argument d'optimisation qui optimisera l'ordre de contraction. Par exemple, np.einsum compléterait l'exemple de points de chaîne np.einsum('ij,jk,kl->il', a, b, c) en un seul passage qui évoluerait comme N^4 ; cependant, lorsque optimise=True, np.einsum créera un tableau intermédiaire pour réduire cette mise à l'échelle à N^3 ou effectivement np.dot(a, b).dot(c). L'utilisation de tenseurs intermédiaires pour réduire la mise à l'échelle a été appliquée à la notation générale de sommation einsum. Voir np.einsum_path pour plus de détails.

Pour aggraver le mystère, certaines notes de version ultérieures indiquent que np.einsum a été mis à niveau pour utiliser Tensordot (qui lui-même utilise BLAS le cas échéant). Maintenant, cela semble prometteur.

Mais alors, pourquoi voyons-nous seulement l'accélération lorsque l'optimisation est Vrai ? Que se passe-t-il ?

Si nous lisons def einsum(*operands, out=None, optimise=False, **kwargs) dans numpy/numpy/_core/einsumfunc.py, nous arriverons presque immédiatement à cette logique de sortie anticipée :

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

Est-ce que c_einsum utilise le tensordot ? J'en doute. Plus loin dans le code, nous voyons l'appel tensordot auquel les notes 1.14 semblent faire référence :

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

Alors, voici ce qui se passe :

1. La boucle contraction_list est exécutée si optimise est True - même dans le cas trivial à deux opérandes.
2. tensordot est uniquement invoqué dans la boucle contraction_list.
3. Par conséquent, nous invoquons tensordot (et donc BLAS) lorsque l'optimisation est True.

Pour moi, cela ressemble à un bug. À mon humble avis, le "early-out" au début de np.einsum devrait toujours détecter si les opérandes sont compatibles avec le tensordot et appeler le tensordot si possible. Ensuite, nous obtiendrons les accélérations BLAS évidentes même lorsque l'optimisation est False. Après tout, la sémantique d'optimisation concerne l'ordre de contraction, pas l'utilisation de BLAS, qui, je pense, devrait être une évidence.

L'avantage ici est que les personnes invoquant np.einsum pour des opérations équivalentes à une invocation tensordot obtiendraient les accélérations appropriées, ce qui rend np.einsum un peu moins dangereux du point de vue des performances.

Concrètement, comment fonctionne c_einsum ?

J'ai spéléographié du code C pour le vérifier. Le cœur de la mise en œuvre est ici.

Après de nombreuses analyses d'arguments et préparation des paramètres, l'ordre d'itération des axes est déterminé et un itérateur spécial est préparé. Chaque rendement de l'itérateur représente une manière différente de parcourir tous les opérandes simultanément.

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

En supposant que certaines optimisations de cas particuliers ne s'appliquent pas, une fonction de somme de produits (sop) appropriée est déterminée en fonction des types de données impliqués :

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

Et puis, cette opération de somme de produits (sop) est invoquée à chaque foulée multi-opérande renvoyée par l'itérateur, comme on le voit ici :

    /* Allocate the iterator */
    iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
                               op_dtypes, ndim_iter, op_axes, NULL, 0);

C'est ma compréhension du fonctionnement de l'einsum, qui est certes encore un peu mince - il mérite vraiment plus que l'heure que je lui ai accordée.

Mais cela confirme cependant mes soupçons, selon lesquels il agit comme une version généralisée et gigabrain de la méthode de multiplication matricielle de l'école primaire. En fin de compte, il délègue à une série d'opérations de « somme de produit » qui reposent sur des « marcheurs » se déplaçant à travers les opérandes – pas très différent de ce que vous faites avec vos doigts lorsque vous apprenez la multiplication matricielle.

Résumé

Alors pourquoi np.einsum généralement est-il plus rapide lorsque vous l'appelez avec optimise=True ? Il y a deux raisons.

La première (et originale) raison est qu'il essaie de trouver un chemin de contraction optimal. Cependant, comme je l'ai souligné, cela ne devrait pas avoir d'importance lorsque nous n'avons que deux opérandes, comme nous le faisons dans nos tests de performances.

La deuxième raison (et plus récente) est que lorsque optimise = True, même dans le cas de deux opérandes, il active un chemin de code qui appelle Tensordot lorsque cela est possible, qui à son tour essaie d'utiliser BLAS. Et BLAS est aussi optimisé que la multiplication matricielle !

Le mystère de l'accélération à deux opérandes est donc résolu ! Cependant, nous n'avons pas vraiment abordé les caractéristiques de l'accélération due à l'ordre de contraction. Cela devra attendre un prochain post ! Restez à l'écoute !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!