Trouver le diamètre minimum après la fusion de deux arbres

3203. Trouver le diamètre minimum après la fusion de deux arbres

Difficulté : Difficile

Sujets : Arbre, recherche en profondeur d'abord, recherche en largeur d'abord, graphique

Il existe deux arbres non orientés avec n et m nœuds, numérotés de 0 à n - 1 et de 0 à m - 1, respectivement. Vous recevez deux tableaux d'entiers 2D Edge1 et Edge2 de longueurs n - 1 et m - 1, respectivement, où Edges1[i] = [a_i, b_i] indique qu'il y a est une arête entre les nœuds a_i et b_i dans le premier arbre et edge2[i] = [u_i, v_i] indique qu'il y a une arête entre les nœuds u_i et v_i dans le deuxième arbre.

Vous devez connecter un nœud du premier arbre avec un autre nœud du deuxième arbre avec une arête.

Renvoyer le minimum diamètre possible de l'arbre résultant.

Le diamètre d'un arbre est la longueur du le plus long chemin entre deux nœuds quelconques de l'arbre.

Exemple 1 :

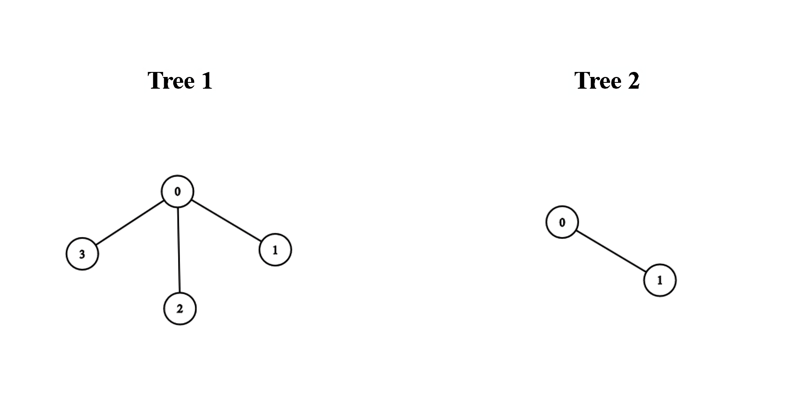
• Entrée : bords1 = [[0,1],[0,2],[0,3]], bords2 = [[0,1]]
• Sortie : 3
• Explication : On peut obtenir un arbre de diamètre 3 en connectant le nœud 0 du premier arbre avec n'importe quel nœud du deuxième arbre.

Exemple 2 :

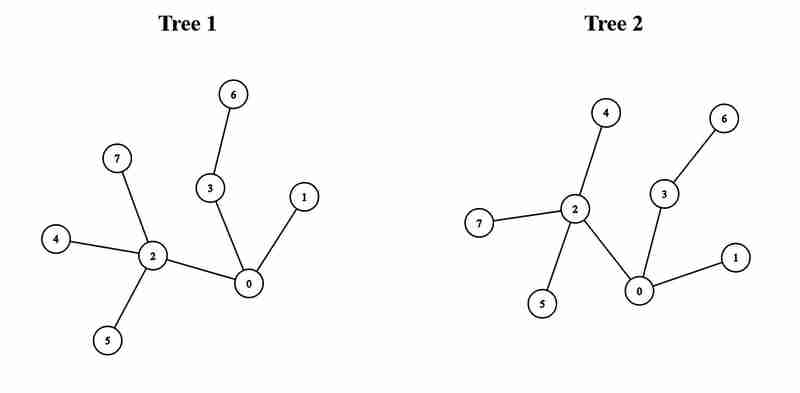
• Entrée : bords1 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2, 7]], bords2 = [[0,1],[0,2],[0,3],[2,4],[2,5],[3,6],[2,7]]
• Sortie : 5
• Explication : On peut obtenir un arbre de diamètre 5 en connectant le nœud 0 du premier arbre avec le nœud 0 du deuxième arbre.

Contraintes :

• 1 <= n, m <= 10⁵
• edges1.length == n - 1
• edges2.length == m - 1
• bords1[i].length == bords2[i].length == 2
• bords1[i] = [a_i, b_i]
• 0 <= a_i, b_i < n
• bords2[i] = [u_i, v_i]
• 0 <= u_i, v_i < m
• L'entrée est générée de telle sorte que les bords1 et les bords2 représentent des arbres valides.

Indice :

1. Supposons que nous connections le nœud a de l'arbre 1 au nœud b de l'arbre 2. La longueur du diamètre de l'arbre résultant sera la plus grande des 3 valeurs suivantes :
   1. Le diamètre de l'arbre 1.
   2. Le diamètre de l'arbre 2.
   3. La longueur du chemin le plus long qui commence au nœud a et qui est complètement dans l'arbre 1. La longueur du chemin le plus long qui commence au nœud b et qui est complètement dans l'arbre 2 1.
   4. Celui ajouté dans la troisième valeur est dû à l'arête supplémentaire que nous avons ajoutée entre les arbres 1 et 2.
2. Les valeurs 1 et 2 sont constantes quel que soit notre choix de a et b. Par conséquent, nous devons choisir a et b de manière à minimiser la valeur 3.
3. Si nous choisissons a et b de manière optimale, ils auront respectivement les diamètres de l'arbre 1 et de l'arbre 2. Quels nœuds du diamètre devons-nous choisir exactement ?
4. a est le centre du diamètre de l'arbre 1 et b est le centre du diamètre de l'arbre 2.

Solution :

Nous devons l'aborder étape par étape en nous concentrant sur la compréhension de la manière de calculer le diamètre d'un arbre et de la manière dont la connexion des deux arbres influence le diamètre total.

Étapes à résoudre :

1. Trouver le diamètre de chaque arbre:

   • Le diamètre d'un arbre est le chemin le plus long entre deux nœuds quelconques. Pour le trouver, nous pouvons utiliser le processus en deux étapes suivant :
     1. Effectuez un BFS (ou DFS) à partir d'un nœud arbitraire pour trouver le nœud le plus éloigné (appelons ce nœud A).
     2. Effectuez un autre BFS (ou DFS) en partant de A pour trouver le nœud le plus éloigné de A (appelons ce nœud B), et la distance de A à B sera le diamètre de l'arbre.

2. Déterminer les nœuds optimaux à connecter :

   • D'après l'indice du problème, la meilleure façon de minimiser le diamètre supplémentaire lors de la connexion de deux arbres est de relier les centres des diamètres des deux arbres. Cela minimisera le chemin le plus long provoqué par le nouveau bord.
   • Le nœud optimal dans le diamètre d'un arbre est généralement le "centre", qui peut être trouvé en effectuant un BFS à partir des extrémités du diamètre et en trouvant le milieu du chemin le plus long.

3. Minimiser le diamètre total :

   • Une fois que nous avons trouvé les centres des deux arbres, le nouveau diamètre est le maximum de :
     • Le diamètre de l'arbre 1.
     • Le diamètre de l'arbre 2.
     • La somme du chemin le plus long dans l'arbre 1, du chemin le plus long dans l'arbre 2 et 1 pour le nouveau bord de connexion.

Implémentons cette solution en PHP : 3203. Trouver le diamètre minimum après la fusion de deux arbres

  
  
  Explication:



Fonction d'assistance BFS : La fonction bfs calcule le nœud le plus éloigné d'un nœud de départ donné et renvoie le tableau de distance et le nœud le plus éloigné trouvé. Ceci est indispensable pour calculer le diamètre de l'arbre.
Obtenir le diamètre et le centre : La fonction getDiameterAndCenter trouve le diamètre d'un arbre et son centre. Le centre de l'arbre est crucial pour minimiser le diamètre du nouvel arbre lors de la fusion de deux arbres.

Solution principale :


Nous construisons d'abord des listes de contiguïté pour les deux arbres.
Nous calculons le diamètre et le centre des deux arbres.
Nous effectuons le BFS à partir des centres des deux arbres pour obtenir les chemins les plus longs au sein de chaque arbre.
Enfin, on calcule le maximum des trois valeurs pour obtenir le diamètre minimum de l'arbre fusionné.





  
  
  Complexité temporelle :



Construction de la liste de contiguïté : O(n m)
Parcours BFS : O(n m)
La complexité temporelle globale est O(n m), ce qui est efficace pour la limite de taille d'entrée de 105.


Cette approche garantit que nous trouvons le diamètre minimum possible lors de la fusion des deux arbres.

Liens de contact

Si vous avez trouvé cette série utile, pensez à donner une étoile au référentiel sur GitHub ou à partager la publication sur vos réseaux sociaux préférés ?. Votre soutien signifierait beaucoup pour moi !

Si vous souhaitez du contenu plus utile comme celui-ci, n'hésitez pas à me suivre :


LinkedIn
GitHub



          

            
  

            
        
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!