Escalader une colline de recherche en profondeur, Advent of Code, jour 10

Le défi d'aujourd'hui aborde le puzzle du jour 10, une grille 2D similaire à celle du jour 6, mais nécessitant l'exploration de plusieurs chemins. Ce puzzle met en valeur avec élégance la puissance de la recherche en profondeur (DFS).

Une illustration du puzzle générée par l'IA

La carte est représentée comme un dictionnaire ; les clés sont les coordonnées (x, y) et les valeurs sont des entiers à un chiffre (0-9) indiquant la hauteur, 9 représentant le pic. La fonction d'analyse gère efficacement cette structure de données :

<code class="language-python">def parse(input: str) -> dict[tuple[int, int], int | None]:
    return {
        (x, y): int(item) if item.isdigit() else None
        for y, row in enumerate(input.strip().splitlines())
        for x, item in enumerate(row)
    }</code>

Les sentiers montent depuis le début du sentier (hauteur 0) jusqu'au sommet (hauteur 9), augmentant la hauteur d'exactement 1 par marche. La fonction next_step identifie les prochaines étapes valides :

<code class="language-python">TRAIL_MAX = 9

def next_step(
    topo_map: dict[tuple[int, int], int | None], x: int, y: int
) -> tuple[tuple[int, int], ...]:
    assert topo_map[(x, y)] != TRAIL_MAX

    return tuple(
        incoming
        for incoming in (
            (x + 1, y),
            (x, y + 1),
            (x - 1, y),
            (x, y - 1),
        )
        if (
            isinstance(topo_map.get(incoming), int)
            and isinstance(topo_map.get((x, y)), int)
            and (topo_map[incoming] - topo_map[(x, y)] == 1)
        )
    )</code>

Les points de départ des sentiers (hauteur 0) sont localisés à l'aide de find_trailheads :

<code class="language-python">TRAILHEAD = 0

def find_trailheads(
    topo_map: dict[tuple[int, int], int | None],
) -> tuple[tuple[int, int], ...]:
    return tuple(key for key, value in topo_map.items() if value == TRAILHEAD)</code>

Le cœur de la solution est la fonction climb, qui implémente une recherche en profondeur d'abord. Suivant la définition de DFS donnée par Wikipédia, nous explorons entièrement chaque branche avant de revenir en arrière.

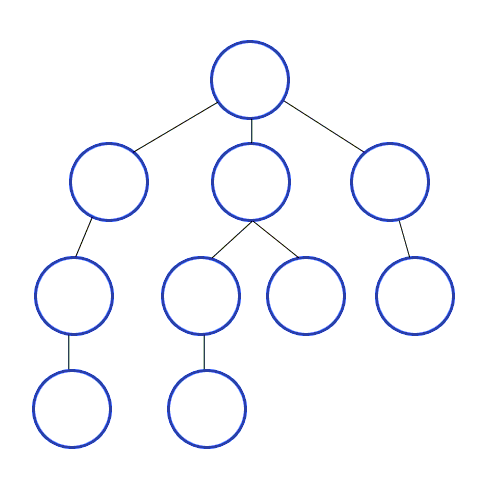
Une représentation visuelle de la recherche en profondeur

Les points de la carte sont nos « nœuds » et nous montons un niveau de hauteur à la fois. La fonction climb gère le processus DFS :

<code class="language-python">def climb(
    topo_map: dict[tuple[int, int], int | None], trailheads: tuple[tuple[int, int], ...]
) -> dict[
    tuple[tuple[int, int], tuple[int, int]], tuple[tuple[tuple[int, int], ...], ...]
]:
    candidates: list[tuple[tuple[int, int], ...]] = [(head,) for head in trailheads]

    result = {}

    while candidates:
        current = candidates.pop()
        while True:
            if topo_map[current[-1]] == TRAIL_MAX:
                result[(current[0], current[-1])] = result.get(
                    (current[0], current[-1]), ()
                ) + (current,)
                break

            elif steps := next_step(topo_map, *current[-1]):
                incoming, *rest = steps

                candidates.extend([current + (step,) for step in rest])

                current = current + (incoming,)
            else:
                break

    return result</code>

La clause else break gère les impasses, empêchant les boucles infinies. La fonction renvoie tous les chemins depuis chaque début de sentier jusqu'au sommet.

La partie 1 compte les destinations de pointe uniques :

<code class="language-python">def part1(input: str) -> int:
    topo_map = parse(input)

    return len(climb(topo_map, find_trailheads(topo_map)))</code>

La partie 2 compte tous les chemins uniques :

<code class="language-python">def part2(input: str) -> int:
    topo_map = parse(input)

    return sum(
        len(routes) for routes in climb(topo_map, find_trailheads(topo_map)).values()
    )</code>

Bien que des approches alternatives existent (par exemple, intégrer la détection des débuts de sentier dans l'analyse), les performances de cette solution sont acceptables. Les récents revers dans la recherche d’emploi ne m’ont pas refroidi le moral ; Je garde espoir. Si vous recherchez un développeur Python de niveau intermédiaire, veuillez nous contacter. A la semaine prochaine !

Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!