PHP Master | Structures de données pour les développeurs PHP: graphiques-tutoriel php-php.cn

PHP Master | Structures de données pour les développeurs PHP: graphiques

Les plats clés

Les graphiques sont des constructions mathématiques utilisées pour modéliser les relations entre les paires de clés / valeur et ont de nombreuses applications du monde réel tels que l'optimisation du réseau, le routage du trafic et l'analyse des réseaux sociaux. Ils sont constitués de sommets (nœuds) et de bords (lignes) qui les connectent, qui peuvent être dirigés ou non dirigés, pondérés ou non pondérés.
Les graphiques peuvent être représentés de deux manières: en tant que matrice d'adjacence ou liste d'adjacence. Les listes d'adjacence sont plus économes en espace, en particulier pour les graphiques clairsemés où la plupart des paires de sommets ne sont pas connectées, tandis que les matrices d'adjacence facilitent les recherches plus rapides.
Une application commune de la théorie des graphiques est de trouver le moins de houblon (c'est-à-dire le chemin le plus court) entre deux nœuds. Cela peut être réalisé en utilisant la recherche en largeur, ce qui implique de traverser le niveau du graphique par niveau à partir d'un nœud racine désigné. Ce processus nécessite de maintenir une file d'attente de nœuds non visités.
est largement utilisé pour trouver le chemin le plus court ou le plus optimal entre deux nœuds dans un graphique. Cela consiste à examiner chaque bord entre toutes les paires de sommets possibles, à partir du nœud source et à maintenir un ensemble de sommets mis à jour avec la distance totale la plus courte jusqu'à ce que le nœud cible soit atteint.

Dans l'un de mes articles précédents, je vous ai présenté la structure des données de l'arbre. Maintenant, je voudrais explorer une structure connexe - le graphique. Les graphiques ont un certain nombre d'applications du monde réel, telles que l'optimisation du réseau, le routage du trafic et l'analyse des réseaux sociaux. Le PageRank de Google, la recherche de graphiques de Facebook et les recommandations d'Amazon et de Netflix sont quelques exemples d'applications axées sur les graphiques. Dans cet article, je vais explorer deux problèmes courants dans lesquels les graphiques sont utilisés - le moins de houblon et les problèmes les plus courts. Un graphique est une construction mathématique utilisée pour modéliser les relations entre les paires de clés / valeur. Un graphique comprend un ensemble de sommets (nœuds) et un nombre arbitraire de bords (lignes) qui les connectent. Ces bords peuvent être dirigés ou non dirigés. Un bord dirigé est simplement un bord entre deux sommets, et le bord A → B n'est pas considéré comme le même que B → A. Un bord non dirigé n'a pas d'orientation ni de direction; Le bord A-B équivaut à B-A. Une structure d'arbre que nous avons apprise sur la dernière fois peut être considérée comme un type de graphique non dirigé, où chaque sommet est connecté à au moins un autre sommet par un chemin simple. Les graphiques peuvent également être pondérés ou non pondérés. Un graphique pondéré, ou un réseau, est celui dans lequel un poids ou une valeur de coût est attribué à chacun de ses bords. Les graphiques pondérés sont couramment utilisés pour déterminer le chemin le plus optimal, le plus opportun ou le plus bas chemin de «coût» entre deux points. Les itinéraires de Googlemap sont un exemple qui utilise des graphiques pondérés.

le moins de houblon

Une application commune de la théorie des graphiques est de trouver le moins de houblon entre deux nœuds. Comme pour les arbres, les graphiques peuvent être traversés de deux manières: profondeur en profondeur ou étendue. Nous avons couvert la recherche en profondeur d'abord dans l'article précédent, alors jetons un coup d'œil à la recherche en première vitesse. Considérez le graphique suivant:

PHP Master | Structures de données pour les développeurs PHP: graphiques

Par souci de simplicité, supposons que le graphique est non dirigé - c'est-à-dire que les bords dans n'importe quelle direction sont identiques. Notre tâche consiste à trouver le moins de houblon entre deux nœuds. Dans une recherche en largeur, nous commençons par le nœud racine (ou tout nœud désigné comme racine) et nous dirigeons vers le niveau de l'arbre par niveau. Pour ce faire, nous avons besoin d'une file d'attente pour maintenir une liste de nœuds non visités afin que nous puissions revenir en arrière et les traiter après chaque niveau. L'algorithme général ressemble à ceci:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Copier après la connexion

Mais comment savons-nous quels nœuds sont adjacents, et encore moins non visités, sans traverser le graphique en premier? Cela nous amène au problème de la façon dont une structure de données graphique peut être modélisée.

représentant le graphique

Il existe généralement deux façons de représenter un graphique: soit en tant que matrice d'adjacence, soit comme liste d'adjacence. Le graphique ci-dessus représenté comme une liste d'adjacence ressemble à ceci:

PHP Master | Structures de données pour les développeurs PHP: graphiques

Représenté comme une matrice, le graphique ressemble à ceci, où 1 indique une «incidence» d'un bord entre 2 sommets:

PHP Master | Structures de données pour les développeurs PHP: graphiques

Les listes d'adjacence sont plus économes en espace, en particulier pour les graphiques clairsemés dans lesquels la plupart des paires de sommets ne sont pas connectées, tandis que les matrices d'adjacence facilitent les recherches plus rapides. En fin de compte, le choix de la représentation dépendra du type d'opérations graphiques qui seront probablement nécessaires. Utilisons une liste d'adjacence pour représenter le graphique:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Copier après la connexion

Et maintenant, voyons à quoi ressemble l'implémentation générale de l'étendue de l'étendue de la recherche:

<span><span><?php
</span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span>

Copier après la connexion

Exécutant les exemples suivants, nous obtenons:

<span><span><?php
</span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span>

Copier après la connexion

Si nous avions utilisé une pile au lieu d'une file d'attente, la traversée devient une recherche en profondeur d'abord.

Trouver le chemin le plus court

Un autre problème courant est de trouver le chemin le plus optimal entre deux nœuds. Plus tôt, j'ai mentionné les itinéraires de Googlemap comme exemple de cela. Les autres applications comprennent la planification des itinéraires de voyage, la gestion du trafic routier et la planification des trains / bus. L'un des algorithmes les plus célèbres pour résoudre ce problème a été inventé en 1959 par un informaticien de 29 ans par le nom d'Edsger W. Dijkstra. En termes généraux, la solution de Dijkstra consiste à examiner chaque bord entre toutes les paires de sommets possibles à partir du nœud source et à maintenir un ensemble de sommets mis à jour avec la distance totale la plus courte jusqu'à ce que le nœud cible soit atteint, ou non atteint, quel que soit le cas. Il existe plusieurs façons de mettre en œuvre la solution, et en effet, au cours des années après 1959, de nombreuses améliorations - en utilisant Minheaps, des PriorityQuues et des Fibonacci Heaps - ont été conçues sur l'algorithme d'origine de Dijkstra. Certaines performances améliorées, tandis que d'autres ont été conçues pour répondre aux lacunes dans la solution de Dijkstra, car elle n'a fonctionné qu'avec des graphiques pondérés positifs (où les poids sont des valeurs positives). Voici un exemple de graphique pondéré (positif):

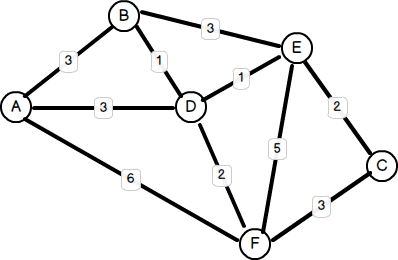
PHP Master | Structures de données pour les développeurs PHP: graphiques

Nous pouvons représenter ce graphique comme une liste d'adjacence, comme suit:

1. Create a queue
2. Enqueue the root node and mark it as visited
3. While the queue is not empty do:
  3a. dequeue the current node
  3b. if the current node is the one we're looking for then stop
  3c. else enqueue each unvisited adjacent node and mark as visited

Copier après la connexion

Et voici une implémentation utilisant une PriorityQueue pour maintenir une liste de tous les sommets «non optimisés»:

<span><span><?php
</span></span><span><span>$graph = array(
</span></span><span>  <span>'A' => array('B', 'F'),
</span></span><span>  <span>'B' => array('A', 'D', 'E'),
</span></span><span>  <span>'C' => array('F'),
</span></span><span>  <span>'D' => array('B', 'E'),
</span></span><span>  <span>'E' => array('B', 'D', 'F'),
</span></span><span>  <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span>

Copier après la connexion

Comme vous pouvez le voir, la solution de Dijkstra est simplement une variation de l'étendue-première recherche! L'exécution des exemples suivants donne les résultats suivants:

<span><span><?php
</span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span>  <span>protected $graph;
</span></span><span>  <span>protected $visited = array();
</span></span><span>
</span><span>  <span>public function __construct($graph) {
</span></span><span>    <span>$this->graph = $graph;
</span></span><span>  <span>}
</span></span><span>
</span><span>  <span>// find least number of hops (edges) between 2 nodes
</span></span><span>  <span>// (vertices)
</span></span><span>  <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span>    <span>// mark all nodes as unvisited
</span></span><span>    <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span>      <span>$this->visited[$vertex] = false;
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>// create an empty queue
</span></span><span>    <span>$q = new SplQueue();
</span></span><span>
</span><span>    <span>// enqueue the origin vertex and mark as visited
</span></span><span>    <span>$q->enqueue($origin);
</span></span><span>    <span>$this->visited[$origin] = true;
</span></span><span>
</span><span>    <span>// this is used to track the path back from each node
</span></span><span>    <span>$path = array();
</span></span><span>    <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span>    <span>$path[$origin]->setIteratorMode(
</span></span><span>      <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span>    <span>);
</span></span><span>
</span><span>    <span>$path[$origin]->push($origin);
</span></span><span>
</span><span>    <span>$found = false;
</span></span><span>    <span>// while queue is not empty and destination not found
</span></span><span>    <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span>      <span>$t = $q->dequeue();
</span></span><span>
</span><span>      <span>if (!empty($this->graph[$t])) {
</span></span><span>        <span>// for each adjacent neighbor
</span></span><span>        <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span>          <span>if (!$this->visited[$vertex]) {
</span></span><span>            <span>// if not yet visited, enqueue vertex and mark
</span></span><span>            <span>// as visited
</span></span><span>            <span>$q->enqueue($vertex);
</span></span><span>            <span>$this->visited[$vertex] = true;
</span></span><span>            <span>// add vertex to current path
</span></span><span>            <span>$path[$vertex] = clone $path[$t];
</span></span><span>            <span>$path[$vertex]->push($vertex);
</span></span><span>          <span>}
</span></span><span>        <span>}
</span></span><span>      <span>}
</span></span><span>    <span>}
</span></span><span>
</span><span>    <span>if (isset($path[$destination])) {
</span></span><span>      <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>, 
</span></span><span>        <span>count($path[$destination]) - 1,
</span></span><span>        <span>" hopsn";
</span></span><span>      <span>$sep = '';
</span></span><span>      <span>foreach ($path[$destination] as $vertex) {
</span></span><span>        <span>echo $sep, $vertex;
</span></span><span>        <span>$sep = '->';
</span></span><span>      <span>}
</span></span><span>      <span>echo "n";
</span></span><span>    <span>}
</span></span><span>    <span>else {
</span></span><span>      <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span>    <span>}
</span></span><span>  <span>}
</span></span><span><span>}</span></span>

Copier après la connexion

Résumé

Dans cet article, j'ai introduit les bases de la théorie des graphiques, deux façons de représenter les graphiques et deux problèmes fondamentaux dans l'application de la théorie des graphiques. Je vous ai montré comment une recherche en largeur est utilisée pour trouver le moins de houblon entre deux nœuds, et comment la solution de Dijkstra est utilisée pour trouver le chemin le plus court entre deux nœuds. Image via Fotolia

Questions fréquemment posées (FAQ) sur les graphiques dans les structures de données

Quelle est la différence entre un graphique et un arbre dans les structures de données?

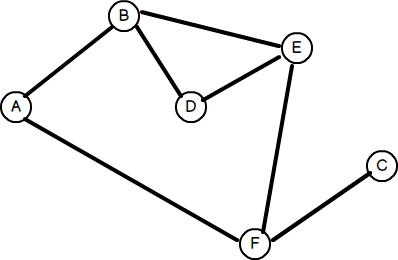
Un graphique et un arbre sont tous deux des structures de données non linéaires, mais elles ont des différences clés. Un arbre est un type de graphique, mais tous les graphiques ne sont pas des arbres. Un arbre est un graphique connecté sans cycles. Il a une structure hiérarchique avec un nœud racine et des nœuds enfants. Chaque nœud d'un arbre a un chemin unique de la racine. D'un autre côté, un graphique peut avoir des cycles et sa structure est plus complexe. Il peut être connecté ou déconnecté et les nœuds peuvent avoir plusieurs chemins entre eux.

Comment les graphiques sont-ils représentés dans les structures de données?

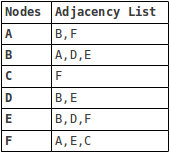
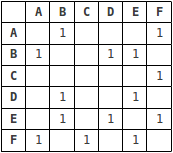
Les graphiques dans les structures de données peuvent être représentés de deux manières: matrice d'adjacence et paradopie liste. Une matrice d'adjacence est un tableau 2D de taille V x V où V est le nombre de sommets dans le graphique. S'il y a un bord entre les sommets I et J, alors la cellule à l'intersection de la ligne I et de la colonne J sera 1, sinon 0. Une liste d'adjacence est un tableau de listes liées. L'indice du tableau représente un sommet et chaque élément de sa liste liée représente les autres sommets qui forment un bord avec le sommet.

Quels sont les types de graphiques dans les structures de données?

sont plusieurs types de graphiques dans les structures de données. Un graphique simple est un graphique sans boucles et pas plus d'un bord entre deux sommets. Un multigraphe peut avoir plusieurs bords entre les sommets. Un graphique complet est un graphique simple où chaque paire de sommets est connectée par un bord. Un graphique pondéré attribue un poids à chaque bord. Un graphique dirigé (ou digraph) a des bords avec une direction. Les bords pointent d'un sommet à un autre.

Quelles sont les applications des graphiques en informatique?

Les graphiques sont utilisés dans de nombreuses applications en informatique. Ils sont utilisés dans les réseaux sociaux pour représenter les liens entre les personnes. Ils sont utilisés dans le flux Web pour visiter les pages Web et créer un index de recherche. Ils sont utilisés dans les algorithmes de routage de réseau pour trouver le meilleur chemin entre deux nœuds. Ils sont utilisés en biologie pour modéliser et analyser les réseaux biologiques. Ils sont également utilisés dans les simulations sur l'infographie et la physique.

Quels sont les algorithmes de traversée graphique?

Il existe deux algorithmes de traversée graphique principaux: recherche en profondeur d'abord (DFS) et largeur d'abord de recherche (BFS). DFS explore autant que possible le long de chaque branche avant de revenir en arrière. Il utilise une structure de données de pile. BFS explore tous les sommets à la profondeur actuelle avant de passer au niveau suivant. Il utilise une structure de données de file d'attente.

Comment implémenter un graphique dans Java?

En Java, un graphique peut être implémenté à l'aide d'un hashmap pour stocker la liste d'adjacence. Chaque clé du hashmap est un sommet et sa valeur est une liste liée contenant les sommets auxquels il est connecté.

Qu'est-ce qu'un graphique bipartite?

Un graphique bipartite est un graphique dont les vertices peuvent être divisé en deux ensembles disjoints tels que chaque bord relie un sommet dans un ensemble sur un sommet dans l'autre ensemble. Aucun bord ne connecte les sommets dans le même ensemble.

Qu'est-ce qu'un sous-graphique?

Un sous-graphique est un graphique qui fait partie d'un autre graphique. Il a des sommets (ou tous) du graphique d'origine et des (ou tous) bords du graphique d'origine.