Deepseek-V3 expliquée 1: Attention latente multi-tête
Deepseek-V3 Explication détaillée Série d'articles: Mécanisme d'attention potentiel des taureaux (MLA)
Cet article est le premier article de la série "Explication détaillée de Deepseek-V3".
Cette série d'articles couvrira deux sujets principaux:
- Les principales innovations architecturales de Deepseek-V3 incluent MLA (Bulner Potential Attention) [3], Deepseekmoe [4], l'équilibrage de la charge sans perte auxiliaire [5] et une formation de prédiction multi-marquée.
- Processus de formation Deepseek-V3, y compris les phases d'alignement d'apprentissage pré-formation, de réglage fin et de renforcement.
Cet article se concentre principalement sur le mécanisme d'attention potentiel multi-tête (MLA) , qui a été initialement proposé dans le développement de Deepseek-V2 et a été appliqué dans Deepseek-V3.
Catalogue:
- CONTEXTE: Nous allons commencer par le MHA standard et expliquer pourquoi le cache de valeur clé est nécessaire pendant la phase d'inférence, comment MQA et GQA essaient de l'optimiser et comment fonctionne la corde, etc.
- Mécanisme de potentiel d'attention (MLA): Introduction approfondie au MLA, y compris ses motivations, pourquoi il doit découpler la corde et ses performances.
- références.
Pour mieux comprendre le MLA et faire cet article un en un, nous passerons en revue plusieurs concepts connexes dans cette section avant de plonger dans les détails de MLA.
MHA dans le transformateur de décodeur
Notez que MLA est développé pour accélérer l'inférence de la génération de texte autorégressive, donc le MHA discuté dans ce contexte est pour le transformateur uniquement du décodeur.
La figure suivante compare trois architectures de transformateur pour le décodage, où (a) montre le codeur et le décodeur proposés dans le papier "l'attention de l'attention est tout ce dont vous avez besoin". La partie de décodeur est ensuite simplifiée par [6] pour obtenir le modèle de transformateur uniquement du décodeur indiqué dans (b), qui a été utilisé plus tard par de nombreux modèles génératifs tels que GPT [8].
Aujourd'hui, les grands modèles de langage choisissent le plus souvent la structure indiquée en (C) pour une formation plus stable, appliquez une normalisation sur les entrées plutôt que sur les sorties, et améliorez la norme Layernor à RMS. Cela servira d'architecture de base dont nous discutons dans cet article.
Dans ce contexte, les calculs MHA suivent largement le processus dans [6], comme le montre la figure ci-dessous: 
Supposons que nous ayons  n_h têtes d'attention, et la dimension de chaque tête d'attention est exprimée comme d_h , donc la dimension connectée sera ( h_n · d_h ).
n_h têtes d'attention, et la dimension de chaque tête d'attention est exprimée comme d_h , donc la dimension connectée sera ( h_n · d_h ).
l calque, si nous représentons l'entrée de la balise T-th dans cette couche comme h_t avec une dimension de d , puis Nous devons utiliser une matrice de mappage linéaire pour cartographier les dimensions de h_t de d à ( h_n · d_h ).
Plus formellement, nous avons (Eq de [3]):  où w ^ q , w ^ k et w ^ v sont des matrices de cartographie linéaires:
où w ^ q , w ^ k et w ^ v sont des matrices de cartographie linéaires:
q_t  , k_t et v_t dans n_h t pour calculer le produit à points proportionnel.
où
, k_t et v_t dans n_h t pour calculer le produit à points proportionnel.
où
est une autre matrice de projection utilisée pour cartographier les dimensions inversement de ( h_n · d_h ) à d :
Notez que les procédures décrites ci-dessus dans l'équation (1) à (8) ne sont que pour un seul marqueur. Pendant le processus de raisonnement, nous devons répéter ce processus pour chaque balisage nouvellement généré, qui implique de nombreux calculs répétés. Cela conduit à une technique appelée mise en cache de valeur clé.
h_n · d_h ) à d :
Notez que les procédures décrites ci-dessus dans l'équation (1) à (8) ne sont que pour un seul marqueur. Pendant le processus de raisonnement, nous devons répéter ce processus pour chaque balisage nouvellement généré, qui implique de nombreux calculs répétés. Cela conduit à une technique appelée mise en cache de valeur clé.
cache de valeur clé 
Notez que le cache KV n'est généralement utilisé que dans la phase d'inférence, car pendant la formation, nous devons encore traiter la séquence d'entrée entière en parallèle.
Le cache
KV est généralement implémenté en tant que tampon de roulement. Dans chaque étape de décodage, seule la nouvelle requête Q est calculée, et les K et V stockés dans le cache seront réutilisés afin de calculer l'attention en utilisant le nouveau Q et Resseuched K et V. Dans le même temps, les nouveaux taggés K et V seront également ajoutés au cache pour une utilisation ultérieure.Cependant, l'accélération apportée par le cache de valeur clé se fait au prix de la mémoire, car les caches de valeur clé varient généralement avec
Taille du lot × longueur de séquence × taille cachée × nombre de têtes
Lorsque nous avons plus grand cela Peut provoquer des goulots d'étranglement de mémoire lorsque la taille ou la séquence du lot est plus longue.Cela conduit en outre à deux techniques conçues pour aborder cette limitation: l'attention multi-remerge et l'attention de la requête en groupe.
Attention à requête multiple (MQA) par rapport à l'attention de groupe (GQA)La figure suivante montre la comparaison entre le MHA d'origine, l'attention de la requête groupée (GQA) [10] et l'attention multi-remery (MQA) [9].
L'idée de base de la MQA est de partager des clés uniques et des en-têtes à valeur unique dans tous les en-têtes de requête, ce qui peut réduire considérablement l'utilisation de la mémoire mais affectera également la précision de l'attention.
GQA peut être considéré comme une méthode d'interpolation entre MHA et MQA, où une seule paire de clés et d'en-têtes de valeur sera partagée par un seul ensemble d'en-têtes de requête, pas toutes les requêtes. Mais cela conduira toujours à des résultats pires que MHA. 
corde (position rotative intégrée)
Le dernier fond que nous devons mentionner est la corde [11], qui code directement sur la position dans le mécanisme d'attention en faisant tourner la requête et les vecteurs clés dans l'attention multi-tête à l'aide d'une fonction sinusoïdale.
Plus précisément, Rope applique la matrice de rotation dépendante de la position à la requête et au vecteur clé de chaque balise et utilise les fonctions sinus et cosinus comme base, mais les applique d'une manière unique pour implémenter Rotate.
Pour comprendre ce qui rend la position dépendante de la position, considérez un vecteur d'intégration de jouets avec seulement 4 éléments, c'est-à-dire (x_1, x_2, x_3, x_4).Pour appliquer une corde, nous regroupons d'abord les dimensions continues en paires:
- (x_1, x_2) - & gt;
- (x_3, x_4) - & gt;
- Ensuite, nous appliquons la matrice de rotation pour faire tourner chaque paire:
où θ = θ (p) = p ⋅ θ_0, et θ_0 est la fréquence fondamentale
. Dans notre exemple de jouet 4D, cela signifie (x_1, x_2) tournera θ_0, tandis que (x_3, x_4) fera tourner 2 ⋅ θ_0.
 C'est pourquoi nous appelons cette matrice de rotation liée à la position : À chaque position (ou chaque paire), nous appliquerons une matrice de rotation différente où l'angle de rotation est déterminé par la position.
C'est pourquoi nous appelons cette matrice de rotation liée à la position : À chaque position (ou chaque paire), nous appliquerons une matrice de rotation différente où l'angle de rotation est déterminé par la position.
est largement utilisée dans les modèles modernes de grande langue en raison de son efficacité dans le codage de longues séquences, mais comme nous pouvons le voir à partir de la formule ci-dessus, il a une sensibilité positionnelle à la fois Q et K, ce qui le rend dans certains aspects incompatibles avec MLA. Mécanisme d'attention potentiel des Bules
Enfin, nous pouvons continuer à discuter de la section MLA. Dans cette section, nous élaborerons d'abord les idées avancées de MLA, puis plongerons pourquoi elle nécessite une modification de la corde. Enfin, nous présenterons également les algorithmes détaillés et leurs performances de MLA.
MLA: pensées avancées
L'idée de base de MLA est de compresser l'attention de l'attention
h_tdans un vecteur laté de faible dimension dont la dimension est
d_c, où d_c est beaucoup plus petit que l'original ( h_n · d_h ). Plus tard, lorsque nous devons calculer l'attention, nous pouvons ramener ce vecteur latent à un espace de haute dimension pour restaurer les clés et les valeurs. Par conséquent, seul le vecteur potentiel doit être stocké, réduisant ainsi considérablement l'utilisation de la mémoire. Ce processus peut être décrit plus formellement avec l'équation suivante, où c ^ {kv} _t est le vecteur latent, et
w ^ {dkv} est à H_T est mappée de ( h_n · d_h ) à la matrice de compression de d_c (D dans l'expositement représente ici "la projection de réduction de la dimensionnalité de dimensionnalité ", ce qui signifie la compression, et w ^ {uk} et w ^ {uv} sont tous deux des matrices de projection supérieures que la carte partageait les vecteurs latents à un espace de haute dimension.
De même, nous pouvons mapper la requête à un vecteur potentiel de basse dimension, puis le ramener à l'espace de haute dimension d'origine: Comme mentionné précédemment, la corde est un choix courant pour la formation de modèles génératifs pour gérer de longues séquences. Si nous appliquons directement la politique MLA ci-dessus, cela sera incompatible avec la corde. Pour voir cela plus clairement, considérons ce qui se passe lorsque nous calculons l'attention en utilisant l'équation. La matrice w ^ q et w ^ {uk} apparaîtra au milieu, et leur combinaison est équivalente à d_c à d un seul Dimension de cartographie pour .
Dans l'article d'origine [3], l'auteur le décrit comme w ^ {uk} qui peut être absorbé par " w ^ q , par conséquent, Nous n'avons pas besoin de stocker w ^ {uk} dans le cache, réduisant ainsi davantage l'utilisation de la mémoire.
Cependant, ce n'est pas le cas lorsque nous considérons la matrice de rotation de la figure (4), car la corde appliquera la matrice de rotation à gauche de w ^ {uk} et cette matrice de rotation finira par être Situé entre w ^ q w ^ {uk} transposé.
Comme nous l'avons expliqué dans la section d'arrière-plan, cette matrice de rotation dépend de la position, ce qui signifie que la matrice de rotation pour chaque position est différente. Par conséquent, w ^ {uk} ** ne peut pas être absorbé par w ^ q ** w ^ q ** .
Pour résoudre ce conflit, les auteurs ont proposé ce qu'ils ont appelé " Corde découplée
L'ensemble du processus MLA peut être résumé comme suit (le numéro d'équation est réutilisé à partir de l'annexe C de [3]):
où
Fait intéressant, les capacités de modélisation de MLA dépassent même celles du MHA d'origine.  ### Pourquoi avez-vous besoin de découpler la corde
### Pourquoi avez-vous besoin de découpler la corde  eqn.
eqn. eqn.
 Plus précisément, le tableau suivant montre les performances de MHA, GQA et MQA sur le modèle 7B, où MHA a des performances nettement meilleures que MQA et GQA.
Plus précisément, le tableau suivant montre les performances de MHA, GQA et MQA sur le modèle 7B, où MHA a des performances nettement meilleures que MQA et GQA.  [3] ont également analysé MHA et MLA, et les résultats sont résumés dans le tableau ci-dessous, où MLA a obtenu de meilleurs résultats dans l'ensemble.
[3] ont également analysé MHA et MLA, et les résultats sont résumés dans le tableau ci-dessous, où MLA a obtenu de meilleurs résultats dans l'ensemble.
 références
références
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1672
1672
 14
14
 1428
1428
 52
52
 1332
1332
 25
25
 1276
1276
 29
29
 1256
1256
 24
24
 Comment construire des agents d'IA multimodaux à l'aide d'AGNO Framework?
Apr 23, 2025 am 11:30 AM
Comment construire des agents d'IA multimodaux à l'aide d'AGNO Framework?
Apr 23, 2025 am 11:30 AM
Tout en travaillant sur une IA agentique, les développeurs se retrouvent souvent à naviguer dans les compromis entre la vitesse, la flexibilité et l'efficacité des ressources. J'ai exploré le cadre de l'IA agentique et je suis tombé sur Agno (plus tôt c'était Phi-
 Comment ajouter une colonne dans SQL? - Analytique Vidhya
Apr 17, 2025 am 11:43 AM
Comment ajouter une colonne dans SQL? - Analytique Vidhya
Apr 17, 2025 am 11:43 AM
Instruction ALTER TABLE de SQL: Ajout de colonnes dynamiquement à votre base de données Dans la gestion des données, l'adaptabilité de SQL est cruciale. Besoin d'ajuster votre structure de base de données à la volée? L'énoncé de la table alter est votre solution. Ce guide détaille l'ajout de Colu
 Openai change de mise au point avec GPT-4.1, priorise le codage et la rentabilité
Apr 16, 2025 am 11:37 AM
Openai change de mise au point avec GPT-4.1, priorise le codage et la rentabilité
Apr 16, 2025 am 11:37 AM
La version comprend trois modèles distincts, GPT-4.1, GPT-4.1 Mini et GPT-4.1 Nano, signalant une évolution vers des optimisations spécifiques à la tâche dans le paysage du modèle grand langage. Ces modèles ne remplacent pas immédiatement les interfaces orientées utilisateur comme
 Nouveau cours court sur les modèles d'intégration par Andrew Ng
Apr 15, 2025 am 11:32 AM
Nouveau cours court sur les modèles d'intégration par Andrew Ng
Apr 15, 2025 am 11:32 AM
Déverrouiller la puissance des modèles d'intégration: une plongée profonde dans le nouveau cours d'Andrew Ng Imaginez un avenir où les machines comprennent et répondent à vos questions avec une précision parfaite. Ce n'est pas de la science-fiction; Grâce aux progrès de l'IA, cela devient un R
 Simulation et analyse de lancement de fusées à l'aide de Rocketpy - Analytics Vidhya
Apr 19, 2025 am 11:12 AM
Simulation et analyse de lancement de fusées à l'aide de Rocketpy - Analytics Vidhya
Apr 19, 2025 am 11:12 AM
Simuler les lancements de fusée avec Rocketpy: un guide complet Cet article vous guide à travers la simulation des lancements de fusées haute puissance à l'aide de Rocketpy, une puissante bibliothèque Python. Nous couvrirons tout, de la définition de composants de fusée à l'analyse de Simula
 Google dévoile la stratégie d'agent la plus complète au cloud prochain 2025
Apr 15, 2025 am 11:14 AM
Google dévoile la stratégie d'agent la plus complète au cloud prochain 2025
Apr 15, 2025 am 11:14 AM
Gemini comme fondement de la stratégie d'IA de Google Gemini est la pierre angulaire de la stratégie d'agent AI de Google, tirant parti de ses capacités multimodales avancées pour traiter et générer des réponses à travers le texte, les images, l'audio, la vidéo et le code. Développé par Deepm
 Robots humanoïdes open source que vous pouvez imprimer vous-même: les câlins de visage achètent la robotique du pollen
Apr 15, 2025 am 11:25 AM
Robots humanoïdes open source que vous pouvez imprimer vous-même: les câlins de visage achètent la robotique du pollen
Apr 15, 2025 am 11:25 AM
"Super heureux d'annoncer que nous acquérons une robotique de pollen pour amener les robots open source au monde", a déclaré Hugging Face sur X. "Depuis que Remi Cadene nous a rejoints de Tesla, nous sommes devenus la plate-forme logicielle la plus utilisée pour la robotique ouverte grâce à des remerciements grâce à des remerciements grâce à des remerciements à une robotique ouverte grâce à des remerciements à des remerciements à des remerciements à la robotique ouverte grâce à des remerciements à Gérom
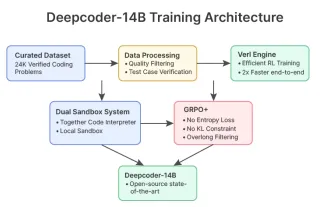 Deepcoder-14b: la compétition open source à O3-MinI et O1
Apr 26, 2025 am 09:07 AM
Deepcoder-14b: la compétition open source à O3-MinI et O1
Apr 26, 2025 am 09:07 AM
Dans un développement significatif pour la communauté de l'IA, Agetica et ensemble AI ont publié un modèle de codage d'IA open source nommé Deepcoder-14b. Offrir des capacités de génération de code à égalité avec des concurrents à source fermée comme OpenAI




