Excel Linest Fonction avec des exemples de formule
Ce tutoriel explique la syntaxe de la fonction Linest et montre comment l'utiliser pour effectuer une analyse de régression linéaire dans Excel.
Microsoft Excel n'est pas un programme statistique, cependant, il a un certain nombre de fonctions statistiques. L'une de ces fonctions est Linest, qui est conçue pour effectuer une analyse de régression linéaire et le retour des statistiques liées. Dans ce didacticiel pour les débutants, nous ne toucherons que légèrement sur la théorie et les calculs sous-jacents. Notre objectif principal sera de vous fournir une formule qui fonctionne simplement et peut être facilement personnalisée pour vos données.
Fonction Excel Linest - Syntaxe et utilisations de base
La fonction Linest calcule les statistiques pour une ligne droite qui explique la relation entre la variable indépendante et une ou plusieurs variables dépendantes, et renvoie un tableau décrivant la ligne. La fonction utilise la méthode des moindres carrés pour trouver le meilleur ajustement pour vos données. L'équation de la ligne est la suivante.
Équation de régression linéaire simple:
y = bx aÉquation de régression multiple:
y = b 1 x 1 b 2 x 2 … b n x n aOù:
- y - la variable dépendante que vous essayez de prédire.
- X - La variable indépendante que vous utilisez pour prédire y .
- A - L'interception (indique où la ligne coupe l'axe y).
- B - La pente (indique la pente de la ligne de régression, c'est-à-dire le taux de variation de Y à mesure que x change).
Dans sa forme de base, la fonction Linest renvoie l'ordonnée (a) et la pente (b) pour l'équation de régression. Facultativement, il peut également renvoyer des statistiques supplémentaires pour l'analyse de régression, comme le montre cet exemple.
Syntaxe de la fonction Linest
La syntaxe de la fonction Excel Linest est la suivante:
Linest (connu_y's, [connu_x], [const], [statistiques])Où:
- Known_y's (requis) est une plage des valeurs y dépendantes dans l'équation de régression. Habituellement, il s'agit d'une seule colonne ou d'une seule ligne.
- Known_X's (Facultatif) est une gamme des valeurs X indépendantes. S'il est omis, il est supposé être le tableau {1,2,3, ...} de la même taille que connu_y .
- const (facultatif) - une valeur logique qui détermine comment l'interception (constante a ) doit être traitée:
- Si elle est vraie ou omise, la constante A est calculée normalement.
- Si faux, la constante A est forcée à 0 et la pente (coefficient B ) est calculée pour s'adapter à y = bx.
- Les statistiques (facultatives) sont une valeur logique qui détermine ou non des statistiques supplémentaires:
- Si vrai, la fonction Linest renvoie un tableau avec des statistiques de régression supplémentaires.
- S'il est faux ou omis, Linest ne renvoie que la constante d'interception et le (s) coefficient (s).
Note. Étant donné que Linest renvoie un tableau de valeurs, il doit être entré sous forme de formule de tableau en appuyant sur le raccourci Entrée Ctrl Shift . S'il est entré en tant que formule régulière, seul le premier coefficient de pente est retourné.
Des statistiques supplémentaires renvoyées par Linest
L'argument des statistiques défini sur True demande à la fonction Linest de renvoyer les statistiques suivantes pour votre analyse de régression:
| Statistique | Description |
| Coefficient de pente | B valeur b en y = bx a |
| Interception constante | une valeur en y = bx a |
| Erreur standard de la pente | La ou les valeurs d'erreur standard pour le (s) coefficient (s) B. |
| Erreur standard d'interception | La valeur d'erreur standard pour la constante a . |
| Coefficient de détermination (r 2 ) | Indique à quel point l'équation de régression explique la relation entre les variables. |
| Erreur standard pour l'estimation Y | Montre la précision de l'analyse de régression. |
| F statistique, ou la valeur observée F | Il est utilisé pour faire le test F pour l'hypothèse nulle afin de déterminer la qualité globale de l'ajustement du modèle. |
| Degrés de liberté (DF) | Le nombre de degrés de liberté. |
| Somme de régression des carrés | Indique la quantité de variation de la variable dépendante est expliquée par le modèle. |
| Somme résiduelle des carrés | Mesure la quantité de variance dans la variable dépendante qui ne s'explique pas par votre modèle de régression. |
La carte ci-dessous montre l'ordre dans lequel Linest renvoie un tableau de statistiques:

Dans les trois dernières lignes, les erreurs # n / a apparaîtront dans les troisième colonnes et suivantes qui ne sont pas remplies de données. C'est le comportement par défaut de la fonction Linest, mais si vous souhaitez masquer les notations d'erreur, enveloppez votre formule Linest dans IFERROR comme indiqué dans cet exemple.
Comment utiliser Linest dans Excel - Exemples de formule
La fonction Linest peut être difficile à utiliser, en particulier pour les novices, car vous devez non seulement créer une formule correctement, mais aussi interpréter correctement sa sortie. Ci-dessous, vous trouverez quelques exemples d'utilisation de formules Linest dans Excel qui, espérons-le, aideront à couler les connaissances théoriques :)
Régression linéaire simple: calculer la pente et l'interception
Pour obtenir l'interception et la pente d'une ligne de régression, vous utilisez la fonction la plus line dans sa forme la plus simple: fournissez une plage de valeurs dépendantes pour l'argument de connu et une plage des valeurs indépendantes pour l'argument de connu_x . Les deux derniers arguments peuvent être définis sur vrai ou omis.
Par exemple, avec les valeurs Y (numéros de vente) dans les valeurs C2: C13 et X (coût publicitaire) en B2: B13, notre formule de régression linéaire est aussi simple que:
=LINEST(C2:C13,B2:B13)
Pour y entrer correctement dans votre feuille de calcul, sélectionnez deux cellules adjacentes dans la même ligne, E2: F2 Dans cet exemple, tapez la formule et appuyez sur Ctrl Shift Entrez pour le terminer.
La formule renverra le coefficient de pente dans la première cellule (E2) et la constante d'interception dans la deuxième cellule (F2):

La pente est d'environ 0,52 (arrondie à deux décimales). Cela signifie que lorsque X augmente de 1, Y augmente de 0,52.
L' ordonnée Y est négative -4,99. C'est la valeur attendue de Y lorsque x = 0. S'il est tracé sur un graphique, c'est la valeur à laquelle la ligne de régression traverse l'axe y.
Fournir les valeurs ci-dessus à une simple équation de régression linéaire, et vous obtiendrez la formule suivante pour prédire le numéro de vente en fonction du coût publicitaire:
y = 0.52*x - 4.99
Par exemple, si vous dépensez 50 $ pour la publicité, vous devez vendre 21 parapluies:
0.52*50 - 4.99 = 21.01
Les valeurs de pente et d'interception peuvent également être obtenues séparément en utilisant la fonction correspondante ou en nichant la formule Linest en index:
Pente
=SLOPE(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),1)
Intercepter
=INTERCEPT(C2:C13,B2:B13)
=INDEX(LINEST(C2:C13,B2:B13),2)
Comme le montre la capture d'écran ci-dessous, les trois formules donnent les mêmes résultats:

Régression linéaire multiple: pente et interception
Dans le cas où vous avez deux variables indépendantes ou plus, assurez-vous de les saisir dans des colonnes adjacentes et fournissez toute cette plage à l'argument de connu_x .
Par exemple, avec les nombres de vente (valeurs Y ) en D2: D13, le coût publicitaire (un ensemble de valeurs x) en B2: B13 et les précipitations mensuelles moyennes (un autre ensemble de valeurs x ) en C2: C13, vous utilisez cette formule:
=LINEST(D2:D13,B2:C13)
Comme la formule va renvoyer un tableau de 3 valeurs (2 coefficients de pente et la constante d'interception), nous sélectionnons trois cellules contiguës dans la même ligne, entrons la formule et appuyons sur le décalage Ctrl Entrez le raccourci.
Veuillez noter que la formule de régression multiple renvoie les coefficients de pente dans l' ordre inverse des variables indépendantes (de droite à gauche), qui est b n , b n-1 ,…, b 2 , b 1 :

Pour prédire le nombre de ventes, nous fournissons les valeurs renvoyées par la formule Linest à l'équation de régression multiple:
y = 0,3 * x 2 0,19 * x 1 - 10,74
Par exemple, avec 50 $ dépensés pour la publicité et des précipitations mensuelles moyennes de 100 mm, vous devez vendre environ 23 parapluies:
0.3*50 0.19*100 - 10.74 = 23.26
Régression linéaire simple: prédire la variable dépendante
En plus de calculer les valeurs A et B pour l'équation de régression, la fonction Excel Linest peut également estimer la variable dépendante (Y) basée sur la variable indépendante connue (x). Pour cela, vous utilisez Linest en combinaison avec la fonction SUM ou SUMPRODUCT.
Par exemple, voici comment vous pouvez calculer le nombre de ventes de parapluies pour le mois prochain, par exemple octobre, sur la base des ventes des mois précédents et du budget publicitaire d'octobre de 50 $:
=SUM(LINEST(C2:C10, B2:B10)*{50,1})

Au lieu de coder en dur la valeur x dans la formule, vous pouvez le fournir comme référence cellulaire. Dans ce cas, vous devez également saisir la constante 1 dans une cellule car vous ne pouvez pas mélanger les références et les valeurs dans une constante de tableau.
Avec la valeur X en E2 et la constante 1 en F2, l'une des formules ci-dessous fonctionnera un régal:
Formule régulière (entrée en appuyant sur Entrée ):
=SUMPRODUCT(LINEST(C2:C10, B2:B10)*(E2:F2))
Formule du tableau (entrée en appuyant sur Ctrl Shift Entrée ):
=SUM(LINEST(C2:C10, B2:B10)*(E2:F2))

Pour vérifier le résultat, vous pouvez obtenir l'interception et la pente pour les mêmes données, puis utiliser la formule de régression linéaire pour calculer Y :
=E2*G2 F2
Où E2 est la pente, G2 est la valeur X et F2 est l'ordonnée:

Régression multiple: prédire la variable dépendante
Dans le cas où vous avez affaire à plusieurs prédicteurs, c'est-à-dire que quelques ensembles différents de valeurs X incluent tous ces prédicteurs dans la constante de tableau. Par exemple, avec le budget publicitaire de 50 $ (x 2 ) et une précipitation mensuelle moyenne de 100 mm (x 1 ), la formule se déroule comme suit:
=SUM(LINEST(D2:D10, B2:C10)*{50,100,1})
Où d2: d10 sont les valeurs y connues et B2: C10 sont deux ensembles de valeurs x :

Veuillez faire attention à l'ordre des valeurs X dans la constante de tableau. Comme indiqué précédemment, lorsque la fonction Excel Linest est utilisée pour effectuer une régression multiple, il renvoie les coefficients de pente de droite à gauche. Dans notre exemple, le coefficient publicitaire est renvoyé en premier, puis le coefficient de précipitations . Pour calculer correctement le nombre de ventes prévu, vous devez multiplier les coefficients par les valeurs x correspondantes, vous mettez donc les éléments de la constante du tableau dans cet ordre: {50,100,1}. Le dernier élément est 1, car la dernière valeur renvoyée par Linest est l'interception qui ne doit pas être modifiée, vous le multipliez donc simplement par 1.
Au lieu d'utiliser une constante de tableau, vous pouvez saisir toutes les variables X dans certaines cellules et faire référence à ces cellules de votre formule comme nous l'avons fait dans l'exemple précédent.
Formule régulière:
=SUMPRODUCT(LINEST(D2:D10, B2:C10)*(F2:H2))
Formule de tableau:
=SUM(LINEST(D2:D10, B2:C10)*(F2:H2))
Où F2 et G2 sont les valeurs X et H2 est 1:

Formule Linest: Statistiques de régression supplémentaires
Comme vous vous en souvenez peut-être, pour obtenir plus de statistiques pour votre analyse de régression, vous mettez vrai dans le dernier argument de la fonction Linest. Appliqué à nos données d'échantillonnage, la formule prend la forme suivante:
=LINEST(D2:D13, B2:C13, TRUE, TRUE)
Comme nous avons 2 variables indépendantes dans les colonnes B et C, nous sélectionnons une rage composée de 3 lignes (deux valeurs x intercepter) et 5 colonnes, entrez la formule ci-dessus, appuyez sur Ctrl Shift Entrée et obtenez ce résultat:

Pour vous débarrasser des erreurs # n / a, vous pouvez nicher Linest dans IFERROR comme ceci:
=IFERROR(LINEST(D2:D13, B2:C13, TRUE, TRUE), "")
La capture d'écran ci-dessous montre le résultat et explique ce que signifie chaque nombre:

Les coefficients de pente et l'ordonnée Y ont été expliqués dans les exemples précédents, alors examinons rapidement les autres statistiques.
Coefficient de détermination (R 2 ). La valeur de R 2 est le résultat de la division de la somme de régression des carrés par la somme totale des carrés. Il vous indique combien de valeurs y sont expliquées par les variables x . Il peut être n'importe quel nombre de 0 à 1, soit 0% à 100%. Dans cet exemple, R 2 est d'environ 0,97, ce qui signifie que 97% de nos variables dépendantes (ventes de parapluies) s'expliquent par les variables indépendantes (publicité mensuelle moyenne), ce qui est un excellent ajustement!
Erreurs standard . Généralement, ces valeurs montrent la précision de l'analyse de régression. Plus les chiffres sont petits, plus vous pouvez être certain de votre modèle de régression.
F statistique . Vous utilisez la statistique F pour soutenir ou rejeter l'hypothèse nulle. Il est recommandé d'utiliser la statistique F en combinaison avec la valeur P lors de la décision si les résultats globaux sont significatifs.
Degrés de liberté (DF). La fonction Linest dans Excel renvoie les degrés de liberté résiduels , qui est le DF total moins la régression DF . Vous pouvez utiliser les degrés de liberté pour obtenir des valeurs critiques F dans un tableau statistique, puis comparer les valeurs critiques F à la statistique F pour déterminer un niveau de confiance pour votre modèle.
Somme de régression des carrés (aka la somme expliquée des carrés , ou la somme modèle des carrés ). C'est la somme des différences carrés entre les valeurs Y prévues et la moyenne de Y, calculée avec cette formule: = ∑ (ŷ - ȳ) 2 . Il indique la part de la variation de la variable dépendante que votre modèle de régression explique.
Somme résiduelle des carrés . C'est la somme des différences carrés entre les valeurs Y réelles et les valeurs Y prévues. Cela indique la part de la variation de la variable dépendante que votre modèle n'explique pas. Plus la somme résiduelle des carrés est petite par rapport à la somme totale des carrés, meilleur est votre modèle de régression correspond à vos données.
5 choses que vous devez savoir sur la fonction Linest
Pour utiliser efficacement les formules Linest dans vos feuilles de travail, vous voudrez peut-être en savoir un peu plus sur les «mécanismes intérieurs» de la fonction:
- Connu_y et connu_x . Dans un modèle de régression linéaire simple avec un seul ensemble de variables X, les connues et les connues peuvent être des gammes de n'importe quelle forme tant qu'ils ont le même nombre de lignes et de colonnes. Si vous effectuez une analyse de régression multiple avec plus d'un ensemble de variables X indépendantes, les connus doivent être un vecteur, c'est-à-dire une gamme d'une ligne ou d'une colonne.
- Forcer la constante à zéro . Lorsque l'argument const est vrai ou est omis, la constante (interception) est calculée et incluse dans l'équation: y = bx a. Si const est défini sur false, l'ordonnée est considérée comme égale 0 et omise de l'équation de régression: y = bx.
Dans les statistiques, il a été débattu depuis des décennies, qu'il soit logique de forcer la constante d'interception à 0 ou non. De nombreux praticiens de l'analyse de régression crédibles croient que si la définition de l'interception à zéro (const = false) semble utile, la régression linéaire elle-même est un mauvais modèle pour l'ensemble de données. D'autres supposent que la constante peut être forcée de zéro dans certaines situations, par exemple, dans le contexte des conceptions de discontinuité de régression. En général, il est recommandé de suivre le const = par défaut True ou omis dans la plupart des cas.
- Précision . La précision de l'équation de régression calculée par la fonction Linest dépend de la dispersion de vos points de données. Plus les données sont linéaires, plus les résultats de la formule Linest.
- Valeurs X redondantes . Dans certaines situations, une ou plusieurs variables X indépendantes peuvent ne pas avoir de valeur prédictive supplémentaire, et la suppression de ces variables du modèle de régression n'affecte pas la précision des valeurs Y prévues. Ce phénomène est connu sous le nom de "colinéarité". La fonction Excel Linest vérifie la colinéarité et omet toutes les variables X redondantes qu'il identifie à partir du modèle. Les variables X omises peuvent être reconnues par 0 coefficients et 0 valeurs d'erreur standard.
- Linest vs pente et interception . L'algorithmique sous-jacent de la fonction la plus line diffère de l'algorithme utilisé dans les fonctions de pente et d'interception. Par conséquent, lorsque les données source sont indéterminées ou colinéaires, ces fonctions peuvent renvoyer différents résultats.
Excel Linest Fonction ne fonctionne pas
Si votre formule Linest lance une erreur ou produit une mauvaise sortie, il est probable que ce soit pour l'une des raisons suivantes:
- Si la fonction Linest ne renvoie qu'un seul numéro (coefficient de pente), vous l'avez très probablement entré en tant que formule régulière, pas une formule de tableau. Assurez-vous d'appuyer sur Ctrl Shift Entrez pour compléter correctement la formule. Lorsque vous faites cela, la formule est enfermée dans les {supports bouclés} qui sont visibles dans la barre de formule.
- #Ref! erreur. Se produit si les gammes connues et connues ont des dimensions différentes.
- #VALEUR! erreur. Se produit si Known_X's ou Know_y's contient au moins une cellule vierge, une valeur de texte ou une représentation de texte d'un nombre qui ne reconnaît pas comme une valeur numérique. De plus, l'erreur #value se produit si l'argument const ou statS ne peut pas être évalué en vrai ou faux.
C'est ainsi que vous utilisez Linest dans Excel pour une analyse de régression linéaire simple et multiple. Pour avoir un examen plus approfondi les formules discutées dans ce tutoriel, vous êtes invités à télécharger notre exemple de classeur ci-dessous. Je vous remercie d'avoir lu et j'espère vous voir sur notre blog la semaine prochaine!
Classeur de pratique pour télécharger
Excel Linest Fonction Exemples (fichier .xlsx)
Ce qui précède est le contenu détaillé de. pour plus d'informations, suivez d'autres articles connexes sur le site Web de PHP en chinois!

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Formule Excel pour trouver des valeurs top 3, 5, 10 dans la colonne ou la ligne
Apr 01, 2025 am 05:09 AM
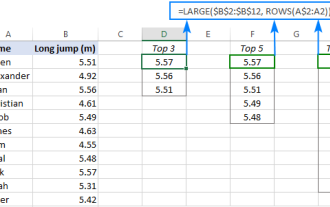
Formule Excel pour trouver des valeurs top 3, 5, 10 dans la colonne ou la ligne
Apr 01, 2025 am 05:09 AM
Ce didacticiel montre comment localiser efficacement les n valeurs supérieures dans un ensemble de données et récupérer les données associées à l'aide de formules Excel. Que vous ayez besoin des critères les plus élevés, les plus bas ou les plus élevés, ce guide fournit des solutions. Findi
 Comment ajouter le calendrier à Outlook: partagé, calendrier Internet, fichier ical
Apr 03, 2025 am 09:06 AM
Comment ajouter le calendrier à Outlook: partagé, calendrier Internet, fichier ical
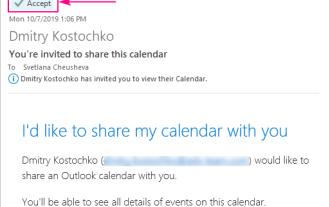
Apr 03, 2025 am 09:06 AM
Cet article explique comment accéder et utiliser des calendriers partagés dans l'application Outlook Desktop, y compris l'importation de fichiers icalEndar. Auparavant, nous avons couvert le partage de votre calendrier Outlook. Maintenant, explorons comment voir les calendriers partagés avec
 Ajouter une liste déroulante sur le modèle d'e-mail Outlook
Apr 01, 2025 am 05:13 AM
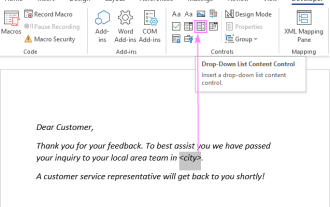
Ajouter une liste déroulante sur le modèle d'e-mail Outlook
Apr 01, 2025 am 05:13 AM
Ce didacticiel vous montre comment ajouter des listes déroulantes à vos modèles de messagerie Outlook, y compris plusieurs sélections et population de bases de données. Bien que Outlook ne prenne pas directement en charge les listes déroulantes, ce guide fournit des solutions créatives. Modèles de messagerie SAV
 Comment utiliser Flash Fill In Excel avec des exemples
Apr 05, 2025 am 09:15 AM
Comment utiliser Flash Fill In Excel avec des exemples
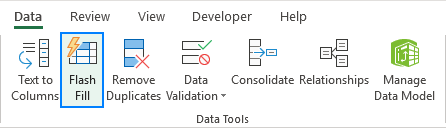
Apr 05, 2025 am 09:15 AM
Ce tutoriel fournit un guide complet de la fonction Flash Fill d'Excel, un outil puissant pour automatiser les tâches de saisie de données. Il couvre divers aspects, de sa définition et de son emplacement à une utilisation et à un dépannage avancées. Comprendre Excel's Fla
 Formule médiane dans Excel - Exemples pratiques
Apr 11, 2025 pm 12:08 PM
Formule médiane dans Excel - Exemples pratiques
Apr 11, 2025 pm 12:08 PM
Ce tutoriel explique comment calculer la médiane des données numériques dans Excel en utilisant la fonction médiane. La médiane, une mesure clé de la tendance centrale, identifie la valeur moyenne dans un ensemble de données, offrant une représentation plus robuste de Central Tenden
 Fonction FV dans Excel pour calculer la valeur future
Apr 01, 2025 am 04:57 AM
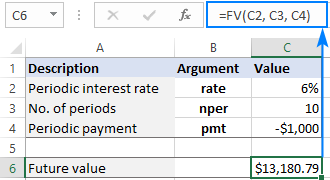
Fonction FV dans Excel pour calculer la valeur future
Apr 01, 2025 am 04:57 AM
Ce tutoriel explique comment utiliser la fonction FV d'Excel pour déterminer la valeur future des investissements, englobant à la fois des paiements réguliers et des dépôts forfaitaires. Une planification financière efficace dépend de la compréhension de la croissance des investissements, et ce guide Prov
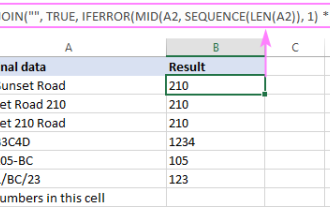 Comment supprimer / diviser le texte et les nombres dans Excel Cell
Apr 01, 2025 am 05:07 AM
Comment supprimer / diviser le texte et les nombres dans Excel Cell
Apr 01, 2025 am 05:07 AM
Ce tutoriel montre plusieurs méthodes de séparation du texte et des nombres dans les cellules Excel, en utilisant à la fois des fonctions intégrées et des fonctions VBA personnalisées. Vous apprendrez à extraire les nombres tout en supprimant le texte, isolez le texte tout en jetant les nombres
 Comment importer des contacts à Outlook (à partir du fichier CSV et PST)
Apr 02, 2025 am 09:09 AM
Comment importer des contacts à Outlook (à partir du fichier CSV et PST)
Apr 02, 2025 am 09:09 AM
Ce didacticiel montre deux méthodes d'importation de contacts dans Outlook: à l'aide de fichiers CSV et PST, et couvre également le transfert de contacts sur Outlook en ligne. Si vous consolidez les données d'une source externe, migrant à partir d'un autre e-mail pro






