邻接矩阵prim:php实现图的邻接矩阵及普里姆(prim算法),弗洛伊德(floyd),迪杰斯特拉(dijkstra)算法
require 'mgraph.php';
$a = array('a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i');
$b = array('ab'=>'10', 'af'=>'11', 'bg'=>'16', 'fg'=>'17', 'bc'=>'18', 'bi'=>'12', 'ci'=>'8', 'cd'=>'22', 'di'=>'21', 'dg'=>'24', 'gh'=>'19', 'dh'=>'16', 'de'=>'20', 'eh'=>'7','fe'=>'26');//键为边,值权值
$test = new mgraph($a, $b);
print_r($test->prim());
?>
mgraph.php
/**
* php 实现图邻接矩阵
*
* @author zhaojiangwei
* @since 2011/10/31 17:23
*/
class mgraph{
private $vexs; //顶点数组
private $arc; //边邻接矩阵,即二维数组
private $arcdata; //边的数组信息
private $direct; //图的类型(无向或有向)
private $haslist; //尝试遍历时存储遍历过的结点
private $queue; //广度优先遍历时存储孩子结点的队列,用数组模仿
private $infinity = 65535;//代表无穷,即两点无连接,建带权值的图时用,本示例不带权值
private $primvexs; //prim算法时保存顶点
private $primarc; //prim算法时保存边
private $krus;//kruscal算法时保存边的信息
public function mgraph($vexs, $arc, $direct = 0){
$this->vexs = $vexs;
$this->arcdata = $arc;
$this->direct = $direct;
$this->initalizearc();
$this->createarc();
}
private function initalizearc(){
foreach($this->vexs as $value){
foreach($this->vexs as $cvalue){
$this->arc[$value][$cvalue] = ($value == $cvalue ? 0 : $this->infinity);
}
}
}
//创建图 $direct:0表示无向图,1表示有向图
private function createarc(){
foreach($this->arcdata as $key=>$value){
$strarr = str_split($key);
$first = $strarr[0];
$last = $strarr[1];
$this->arc[$first][$last] = $value;
if(!$this->direct){
$this->arc[$last][$first] = $value;
}
}
}
//floyd算法
public function floyd(){
$path = array();//路径数组
$distance = array();//距离数组
foreach($this->arc as $key=>$value){
foreach($value as $k=>$v){
$path[$key][$k] = $k;
$distance[$key][$k] = $v;
}
}
for($j = 0; $j vexs); $j ++){
for($i = 0; $i vexs); $i ++){
for($k = 0; $k vexs); $k ++){
if($distance[$this->vexs[$i]][$this->vexs[$k]] > $distance[$this->vexs[$i]][$this->vexs[$j]] + $distance[$this->vexs[$j]][$this->vexs[$k]]){
$path[$this->vexs[$i]][$this->vexs[$k]] = $path[$this->vexs[$i]][$this->vexs[$j]];
$distance[$this->vexs[$i]][$this->vexs[$k]] = $distance[$this->vexs[$i]][$this->vexs[$j]] + $distance[$this->vexs[$j]][$this->vexs[$k]];
}
}
}
}
return array($path, $distance);
}
//djikstra算法
public function dijkstra(){
$final = array();
$pre = array();//要查找的结点的前一个结点数组
$weight = array();//权值和数组
foreach($this->arc[$this->vexs[0]] as $k=>$v){
$final[$k] = 0;
$pre[$k] = $this->vexs[0];
$weight[$k] = $v;
}
$final[$this->vexs[0]] = 1;
for($i = 0; $i vexs); $i ++){
$key = 0;
$min = $this->infinity;
for($j = 1; $j vexs); $j ++){
$temp = $this->vexs[$j];
if($final[$temp] != 1 && $weight[$temp] $key = $temp;
$min = $weight[$temp];
}
}
$final[$key] = 1;
for($j = 0; $j vexs); $j ++){
$temp = $this->vexs[$j];
if($final[$temp] != 1 && ($min + $this->arc[$key][$temp]) $pre[$temp] = $key;
$weight[$temp] = $min + $this->arc[$key][$temp];
}
}
}
return $pre;
}
//kruscal算法
private function kruscal(){
$this->krus = array();
foreach($this->vexs as $value){
$krus[$value] = 0;
}
foreach($this->arc as $key=>$value){
$begin = $this->findroot($key);
foreach($value as $k=>$v){
$end = $this->findroot($k); 本文链接http://www.cxybl.com/html/wlbc/Php/20120607/28507.html

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 1393
1393
 52
52
 1207
1207
 24
24
 Quelles sont les différences entre Huawei GT3 Pro et GT4 ?
Dec 29, 2023 pm 02:27 PM
Quelles sont les différences entre Huawei GT3 Pro et GT4 ?
Dec 29, 2023 pm 02:27 PM
De nombreux utilisateurs choisiront la marque Huawei lors du choix des montres intelligentes. Parmi eux, les Huawei GT3pro et GT4 sont des choix très populaires. De nombreux utilisateurs sont curieux de connaître la différence entre Huawei GT3pro et GT4. Quelles sont les différences entre Huawei GT3pro et GT4 ? 1. Apparence GT4 : 46 mm et 41 mm, le matériau est un miroir en verre + un corps en acier inoxydable + une coque arrière en fibre haute résolution. GT3pro : 46,6 mm et 42,9 mm, le matériau est du verre saphir + corps en titane/corps en céramique + coque arrière en céramique 2. GT4 sain : en utilisant le dernier algorithme Huawei Truseen5.5+, les résultats seront plus précis. GT3pro : ajout d'un électrocardiogramme ECG, d'un vaisseau sanguin et de la sécurité
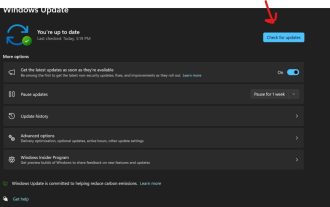 Correctif : l'outil de capture ne fonctionne pas sous Windows 11
Aug 24, 2023 am 09:48 AM
Correctif : l'outil de capture ne fonctionne pas sous Windows 11
Aug 24, 2023 am 09:48 AM
Pourquoi l'outil Snipping ne fonctionne pas sous Windows 11 Comprendre la cause première du problème peut aider à trouver la bonne solution. Voici les principales raisons pour lesquelles l'outil de capture peut ne pas fonctionner correctement : L'assistant de mise au point est activé : cela empêche l'ouverture de l'outil de capture. Application corrompue : si l'outil de capture plante au lancement, il est peut-être corrompu. Pilotes graphiques obsolètes : des pilotes incompatibles peuvent interférer avec l'outil de capture. Interférence provenant d'autres applications : d'autres applications en cours d'exécution peuvent entrer en conflit avec l'outil de capture. Le certificat a expiré : une erreur lors du processus de mise à niveau peut provoquer ce problème. Solution simple. Celles-ci conviennent à la plupart des utilisateurs et ne nécessitent aucune connaissance technique particulière. 1. Mettez à jour les applications Windows et Microsoft Store
 Que signifie privé en Java
Nov 24, 2022 pm 06:27 PM
Que signifie privé en Java
Nov 24, 2022 pm 06:27 PM
En Java, private signifie « privé » et est un modificateur de contrôle d'accès utilisé pour modifier les classes, les propriétés et les méthodes. Les membres de la classe modifiés avec private ne peuvent être consultés et modifiés que par les méthodes de la classe elle-même, et ne peuvent être consultés et référencés par aucune autre classe (y compris les sous-classes de la classe, par conséquent, le modificateur private a le niveau de protection le plus élevé) ;
 Comment réparer l'erreur Impossible de se connecter à l'App Store sur iPhone
Jul 29, 2023 am 08:22 AM
Comment réparer l'erreur Impossible de se connecter à l'App Store sur iPhone
Jul 29, 2023 am 08:22 AM
Partie 1 : étapes de dépannage initiales Vérification de l'état du système Apple : avant d'aborder des solutions complexes, commençons par les bases. Le problème ne vient peut-être pas de votre appareil ; les serveurs Apple sont peut-être en panne. Visitez la page État du système d'Apple pour voir si l'AppStore fonctionne correctement. S'il y a un problème, tout ce que vous pouvez faire est d'attendre qu'Apple le résolve. Vérifiez votre connexion Internet : assurez-vous que vous disposez d'une connexion Internet stable, car le problème "Impossible de se connecter à l'AppStore" peut parfois être attribué à une mauvaise connexion. Essayez de basculer entre le Wi-Fi et les données mobiles ou de réinitialiser les paramètres réseau (Général > Réinitialiser > Réinitialiser les paramètres réseau > Paramètres). Mettez à jour votre version iOS :
 php提交表单通过后,弹出的对话框怎样在当前页弹出,该如何解决
Jun 13, 2016 am 10:23 AM
php提交表单通过后,弹出的对话框怎样在当前页弹出,该如何解决
Jun 13, 2016 am 10:23 AM
php提交表单通过后,弹出的对话框怎样在当前页弹出php提交表单通过后,弹出的对话框怎样在当前页弹出而不是在空白页弹出?想实现这样的效果:而不是空白页弹出:------解决方案--------------------如果你的验证用PHP在后端,那么就用Ajax;仅供参考:HTML code
 Voyons pourquoi Vue2 peut accéder aux attributs dans diverses options via ceci
Dec 08, 2022 pm 08:22 PM
Voyons pourquoi Vue2 peut accéder aux attributs dans diverses options via ceci
Dec 08, 2022 pm 08:22 PM
Cet article vous aidera à interpréter le code source de Vue et à vous expliquer pourquoi vous pouvez l'utiliser pour accéder aux propriétés de diverses options de Vue2. J'espère qu'il sera utile à tout le monde !
 Un article qui comprend ce point et rattrape 70% des front-end
Sep 06, 2022 pm 05:03 PM
Un article qui comprend ce point et rattrape 70% des front-end
Sep 06, 2022 pm 05:03 PM
Un collègue est resté bloqué à cause d'un bug signalé par ce problème de pointage de Vue2 qui a provoqué l'utilisation d'une fonction de flèche, entraînant l'impossibilité d'obtenir les accessoires correspondants. Il ne le savait pas quand je le lui ai présenté, puis j'ai délibérément regardé le groupe de communication front-end. Jusqu'à présent, au moins 70 % des programmeurs front-end ne le comprennent toujours pas. Aujourd'hui, je vais partager avec. vous ce lien. Si tout n'est pas clair Si vous ne l'avez pas encore appris, s'il vous plaît, faites-moi une grande gueule.
 Explication détaillée des modificateurs d'accès privé pour les fonctions Java
Apr 25, 2024 pm 04:48 PM
Explication détaillée des modificateurs d'accès privé pour les fonctions Java
Apr 25, 2024 pm 04:48 PM
Private est un modificateur d'accès Java qui restreint l'accessibilité d'une fonction uniquement à la classe dans laquelle elle est définie, notamment : la fonction n'est pas accessible dans d'autres classes. La fonction n'est pas non plus accessible dans les sous-classes.




