递归删除一个节点以及该节点下的所有节点示例_PHP教程
有的时候删除信息的时候,需要把这条信息下的所有的都删除,这个时候就需要递归删除了。下面是我在做部门管理中的删除部门功能的时候写的一段递归删除一个部门以及它的所有子部门的一段代码。仅供大家参考和自己以后备用。
下面是我的一段代码的展示:
/*
* 修改一条部门信息
*/
function del($bumen_id){
$sql="select bumen_id from lxsm_bumen where topbumen_id=".$bumen_id; //查询以topbumen_id为$bumen_id的bumen_id
$delsql="delete from lxsm_bumen where bumen_id=".$bumen_id; //删除bumen_id为$bumen_id的部门信息
$xiaji_id=$this->DB->fetch_assoc($sql);
if($xiaji_id){
foreach($xiaji_id as $id){
$res=$this->del($id[bumen_id]);
}
}
$result=$this->DB->query($delsql);
if($result){
return true;
}
else{
return false;
}
}
注释:这里的topbumen_id是部门信息中的上级部门的id号,fetch_assoc()函数是自己已经封装好的函数,是把查询得到的所有内容返回成一个数组。
心得体会:这是自己第一次写递归算法,写得还很稚嫩,不管怎样功能是实现了。我感觉写递归方面的代码的时候,自己先画好一个树状结构,认清其结构后,根据自己想要得到的效果,先在脑子里模拟一步一步的执行。比如这里的删除,想要删除一个部门,就得删除自己并且查找以自己为上级部门的子部门有哪些,把子部门一个一个地遍历得到,这时候子部门的操作,就和它的上级部门的删除一样,需要删除自己并且查找它的子部门,这样一来就有个类似重复的操作,子部门的操作和上级部门的操作经历的步骤是一样的,因此在子部门的遍历中让它执行这个本身的函数。这样一来就形成了一个递归算法。

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

AI Hentai Generator
Générez AI Hentai gratuitement.

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)

Sujets chauds
 Interrogez le poids minimum dans le sous-arbre à partir du nœud X et la distance au plus D
Aug 25, 2023 am 11:25 AM
Interrogez le poids minimum dans le sous-arbre à partir du nœud X et la distance au plus D
Aug 25, 2023 am 11:25 AM
Lors de la programmation informatique, il est parfois nécessaire de trouver le poids minimum d'un sous-arbre provenant d'un nœud spécifique, à condition que le sous-arbre ne puisse pas contenir de nœuds éloignés de plus de D unités du nœud spécifié. Ce problème se pose dans divers domaines et applications, notamment la théorie des graphes, les algorithmes arborescents et l'optimisation des réseaux. Un sous-arbre est un sous-ensemble d'une structure arborescente plus grande, le nœud spécifié servant de nœud racine du sous-arbre. Un sous-arbre contient tous les descendants du nœud racine et leurs arêtes de connexion. Le poids d'un nœud fait référence à une valeur spécifique attribuée à ce nœud, qui peut représenter son importance, sa signification ou d'autres mesures pertinentes. Dans ce problème, l’objectif est de trouver le poids minimum parmi tous les nœuds d’un sous-arbre tout en limitant le sous-arbre aux nœuds situés au plus à D unités du nœud racine. Dans l'article suivant, nous approfondirons la complexité de l'extraction des poids minimum des sous-arbres.
 Quelle est la méthode pour supprimer un nœud dans js
Sep 01, 2023 pm 05:00 PM
Quelle est la méthode pour supprimer un nœud dans js
Sep 01, 2023 pm 05:00 PM
Les méthodes de suppression de nœuds dans js sont : 1. La méthode removeChild() est utilisée pour supprimer le nœud enfant spécifié du nœud parent. Elle nécessite deux paramètres. Le premier paramètre est le nœud enfant à supprimer et le deuxième paramètre est. le nœud parent. 2. La méthode parentNode.removeChild() peut être appelée directement via le nœud parent pour supprimer le nœud enfant ; 3. La méthode remove() peut supprimer directement le nœud sans spécifier le nœud parent ; L'attribut innerHTML est utilisé pour supprimer le contenu du nœud.
 Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ?
Aug 15, 2023 pm 05:57 PM
Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ?
Aug 15, 2023 pm 05:57 PM
Comment implémenter les fonctions de copie et de coupure de nœuds des cartes mentales via Vue et jsmind ? La carte mentale est un outil de réflexion courant qui peut nous aider à organiser nos pensées et à trier notre logique de pensée. Les fonctions de copie et de coupe de nœuds sont des opérations couramment utilisées dans les cartes mentales, qui nous permettent de réutiliser plus facilement les nœuds existants et d'améliorer l'efficacité de l'organisation de la réflexion. Dans cet article, nous utiliserons les deux outils Vue et jsmind pour implémenter les fonctions de copie et de coupe de nœuds de la carte mentale. Tout d'abord, nous devons installer Vue et jsmind et créer
 Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
Trouvez le chemin le plus court entre deux nœuds à l'aide de l'algorithme Floyd-Warshal
Sep 20, 2023 pm 02:21 PM
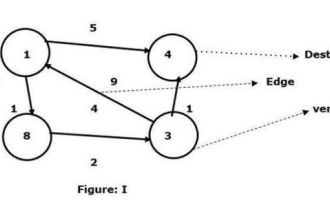
C++ a une macro, qui est définie comme un morceau de code ou une valeur attendue, et elle sera réutilisée chaque fois que l'utilisateur en aura besoin. L'algorithme de Floyd-Walshall est le processus permettant de trouver le chemin le plus court entre toutes les paires de sommets dans un graphe pondéré donné. L'algorithme suit une approche de programmation dynamique pour trouver le graphique de poids minimum. Comprenons la signification de l'algorithme de Floyd-Walshall à travers un diagramme - prenons le sommet 1 comme source et le sommet 4 comme destination et trouvons le chemin le plus court entre eux. Nous avons vu qu'il existe deux chemins qui peuvent être connectés au sommet cible 4. 1->4 – l'arête a un poids de 51->8->3->4 – le poids de l'arête (1+2+1) est 4. Dans le graphique I donné, nous voyons la plus petite arête reliant deux sommets. Voici donc le sommet
 Comment créer, supprimer, ajouter et remplacer des nœuds d'éléments dans js (avec des exemples de code)
Aug 06, 2022 pm 05:26 PM
Comment créer, supprimer, ajouter et remplacer des nœuds d'éléments dans js (avec des exemples de code)
Aug 06, 2022 pm 05:26 PM
Cet article présente principalement comment créer, supprimer, ajouter et remplacer des nœuds d'éléments dans js. J'espère qu'il sera utile aux amis dans le besoin !
 Dans le programme C, traduisez le contenu suivant en chinois : Programme pour trouver le nième nœud à partir du bas d'une liste chaînée
Sep 13, 2023 pm 03:13 PM
Dans le programme C, traduisez le contenu suivant en chinois : Programme pour trouver le nième nœud à partir du bas d'une liste chaînée
Sep 13, 2023 pm 03:13 PM
Étant donné n nœuds, la tâche consiste à imprimer le nième nœud à la fin de la liste chaînée. Le programme ne doit pas modifier l'ordre des nœuds dans la liste, mais doit uniquement imprimer le nième nœud du dernier nœud de la liste chaînée. Exemple d'entrée-:102030405060 N=3Output-:40 Dans l'exemple ci-dessus, en partant du premier nœud, parcourez jusqu'à n nœuds, c'est-à-dire 10,2030,40,50,60, donc l'avant-dernier nœud est 40. . Au lieu de parcourir toute la liste de manière aussi efficace, l'approche que vous pouvez suivre consiste à obtenir un pointeur temporaire vers, par exemple, la température du type de nœud, et à définir ce pointeur temporaire sur le premier nœud pointé par le pointeur principal pour définir le compteur sur celui de la liste.
 Avec le plug-in ChatGPT, c'est un nœud, mais pas un centre
Apr 04, 2023 am 11:45 AM
Avec le plug-in ChatGPT, c'est un nœud, mais pas un centre
Apr 04, 2023 am 11:45 AM
OpenAI est un nœud (bien qu’important) dans le monde du dialogue robot-robot, mais ce n’est pas le centre. ChatGPT a lancé un mécanisme de plugin, ce qui constitue un développement très passionnant. Tout le monde a déclaré à l'unanimité qu'« un système d'exploitation était né ». Cette affirmation est complètement fausse. OpenAI est un nœud (bien qu’important) dans le monde du dialogue robot-robot, mais ce n’est pas le centre. J'ai toujours eu une image en tête : un monde où les robots parlent à des robots. Les gens discutent avec un robot et laissent le robot aider l'humain à accomplir des tâches grâce à ses amis robots. Le plugin ChatGPT démontre parfaitement le monde
 Vérifie si le chemin entre deux nœuds dans le graphique donné représente le chemin le plus court
Sep 07, 2023 pm 06:57 PM
Vérifie si le chemin entre deux nœuds dans le graphique donné représente le chemin le plus court
Sep 07, 2023 pm 06:57 PM
Pour vérifier si un chemin donné entre deux centres d'un graphique est conforme au chemin le plus court, cela peut être calculé en comparant le poids total du bord le long du chemin donné à la distance la plus courte entre des combinaisons des mêmes centres en utilisant un chemin le plus court fiable, tel que Calcul de Dijkstra ou calcul de Floyd-Warshall. Si tous les poids des bords sur un chemin donné correspondent à la suppression la plus limitée, alors cela représente le chemin le plus simple. Également : si le poids global du bord est plus important que la distance la plus courte, cela indique qu'il existe une courte distance entre les deux centres dans le graphique. Méthodes utilisées Algorithme de Dijkstra Algorithme Floyd−Warshall avec coût d'inversion marginal Algorithme gourmand Le calcul de Dijkstra peut être un calcul de parcours de graphe populaire






