 interface Web
interface Web
 js tutoriel
js tutoriel
 Pourquoi js ne peut-il pas gérer correctement les opérations décimales ? _compétences javascript
Pourquoi js ne peut-il pas gérer correctement les opérations décimales ? _compétences javascript
Pourquoi js ne peut-il pas gérer correctement les opérations décimales ? _compétences javascript
var sum = 0;
for(var i = 0; i < 10; i++) {
sum += 0.1;
}
console.log(sum);
Le programme ci-dessus produira-t-il 1 ?
Dans l'article 25 questions d'entretien JavaScript que vous devez connaître , la 8ème question explique brièvement pourquoi js ne peut pas gérer correctement les opérations décimales. Aujourd'hui, je vais revenir sur un vieux sujet et analyser cette question de manière plus approfondie.
Mais tout d'abord, il convient de noter que l'incapacité à gérer correctement les opérations décimales n'est pas une erreur de conception dans le langage JavaScript lui-même. D'autres langages de programmation de haut niveau, tels que C, Java, etc., en sont également incapables. pour gérer correctement les opérations décimales :
#include <stdio.h>
void main(){
float sum;
int i;
sum = 0;
for(i = 0; i < 100; i++) {
sum += 0.1;
}
printf('%f\n', sum); //10.000002
}
Représentation des nombres à l'intérieur de l'ordinateur
Nous savons tous que les programmes écrits dans des langages de programmation de haut niveau doivent être convertis en langage machine pouvant être reconnu par le CPU (Central Processing Unit) via l'interprétation, la compilation et d'autres opérations avant de pouvoir être exécutés. , pour le CPU, il ne reconnaît pas les systèmes de nombres décimaux et décimaux octal et hexadécimal, etc., ces nombres de base que nous déclarons dans le programme seront convertis en nombres binaires pour le calcul.
Pourquoi ne pas le convertir en nombres ternaires pour le calcul ?
L'intérieur d'un ordinateur est composé de nombreux composants électroniques tels que des IC (Integrated Circuit : Integrated Circuit). Il ressemble à ceci :
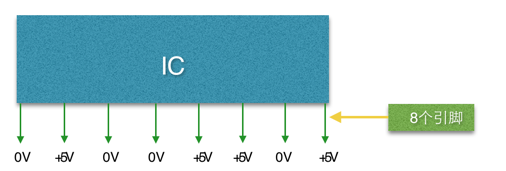
Les circuits intégrés se présentent sous de nombreuses formes, avec de nombreuses broches disposées côte à côte des deux côtés ou à l'intérieur (un seul côté est montré sur l'image). Toutes les broches du circuit intégré n'ont que deux états de tension continue 0 V ou 5 V, c'est-à-dire qu'une broche du circuit intégré ne peut représenter que deux états. Cette caractéristique d'IC détermine que les données contenues dans l'ordinateur ne peuvent être traitées qu'avec des nombres binaires.
Puisque 1 bit (une broche) ne peut représenter que deux états, la méthode de calcul binaire devient 0, 1, 10, 11, 100... Cette forme :
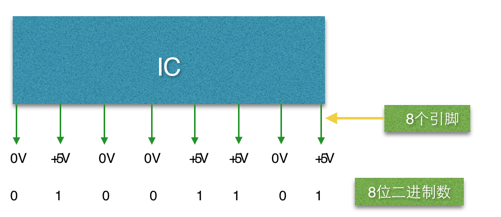
Ainsi, dans les opérations sur les nombres, tous les opérandes seront convertis en nombres binaires pour participer à l'opération, comme 39, sera converti en binaire 00100111
Représentation binaire des décimales
Comme mentionné ci-dessus, les données du programme seront converties en nombres binaires Lorsque des décimales sont impliquées dans des opérations, elles seront également converties en nombres binaires. Par exemple, le nombre décimal 11,1875 sera converti en 1101,0010.
La plage numérique exprimée par 4 chiffres après la virgule dans les nombres binaires est de 0,0000 ~ 0,1111. Par conséquent, cela ne peut représenter que la combinaison (addition) des quatre nombres décimaux 0,5, 0,25, 0,125, 0,0625 et les poids en bits après. le point décimal :

Comme le montre le tableau ci-dessus, le chiffre suivant du nombre décimal 0 est 0,0625. Par conséquent, les décimales entre 0 et 0,0625 ne peuvent pas être représentées par des nombres binaires avec 4 chiffres après la virgule décimale ; le point décimal, le nombre de chiffres décimaux correspondants augmentera également, mais quel que soit le nombre de chiffres ajoutés, le résultat de 0,1 ne peut pas être obtenu. En fait, 0,1 converti en binaire vaut 0,00110011001100110011... Notez que 0011 est répété à l'infini :
console.log(0.2+0.1); //操作数的二进制表示 0.1 => 0.0001 1001 1001 1001…(无限循环) 0.2 => 0.0011 0011 0011 0011…(无限循环)
Le type Number de js n'est pas divisé en entier, simple précision, double précision, etc. comme C/Java, mais est uniformément exprimé comme un type à virgule flottante double précision. Selon la réglementation IEEE, les nombres à virgule flottante simple précision utilisent 32 bits pour représenter toutes les décimales, tandis que les nombres à virgule flottante double précision utilisent 64 bits pour représenter toutes les décimales. Les nombres à virgule flottante sont composés d'un signe, d'une mantisse, d'un exposant et d'une base. , donc tous les chiffres ne sont pas utilisés. Pour représenter des décimales, les symboles, les exposants, etc. doivent également occuper des chiffres, et la base n'occupe pas de chiffres :

La partie décimale d'un nombre à virgule flottante double précision prend en charge jusqu'à 52 chiffres, donc après avoir ajouté les deux, vous obtenez une chaîne de 0,0100110011001100110011001100110011001100... un nombre binaire tronqué en raison de la limitation de la place décimale de le nombre à virgule flottante. À ce moment, convertissez-le en décimal, cela devient 0,30000000000000004.
Résumé
js ne peut pas gérer correctement les opérations décimales, y compris d'autres langages de programmation de haut niveau. Ce n'est pas une erreur de conception du langage lui-même, mais l'ordinateur lui-même ne peut pas gérer correctement les opérations décimales. Les opérations sur les décimales ne produisent souvent pas des résultats inattendus. les fractions décimales peuvent être représentées en binaire.
Ce qui précède représente l’intégralité du contenu de cet article, j’espère qu’il sera utile à l’étude de chacun.

Outils d'IA chauds

Undresser.AI Undress
Application basée sur l'IA pour créer des photos de nu réalistes

AI Clothes Remover
Outil d'IA en ligne pour supprimer les vêtements des photos.

Undress AI Tool
Images de déshabillage gratuites

Clothoff.io
Dissolvant de vêtements AI

Video Face Swap
Échangez les visages dans n'importe quelle vidéo sans effort grâce à notre outil d'échange de visage AI entièrement gratuit !

Article chaud

Outils chauds

Bloc-notes++7.3.1
Éditeur de code facile à utiliser et gratuit

SublimeText3 version chinoise
Version chinoise, très simple à utiliser

Envoyer Studio 13.0.1
Puissant environnement de développement intégré PHP

Dreamweaver CS6
Outils de développement Web visuel

SublimeText3 version Mac
Logiciel d'édition de code au niveau de Dieu (SublimeText3)
 Comment utiliser JS et Baidu Maps pour implémenter la fonction Map Pan
Nov 21, 2023 am 10:00 AM
Comment utiliser JS et Baidu Maps pour implémenter la fonction Map Pan
Nov 21, 2023 am 10:00 AM
Comment utiliser JS et Baidu Map pour implémenter la fonction de panoramique de la carte Baidu Map est une plate-forme de services cartographiques largement utilisée, souvent utilisée pour afficher des informations géographiques, le positionnement et d'autres fonctions dans le développement Web. Cet article explique comment utiliser JS et l'API Baidu Map pour implémenter la fonction de panoramique de la carte et fournit des exemples de code spécifiques. 1. Préparation Avant d'utiliser l'API Baidu Map, vous devez d'abord demander un compte de développeur sur Baidu Map Open Platform (http://lbsyun.baidu.com/) et créer une application. Création terminée
 Recommandé : Excellent projet de détection et de reconnaissance des visages open source JS
Apr 03, 2024 am 11:55 AM
Recommandé : Excellent projet de détection et de reconnaissance des visages open source JS
Apr 03, 2024 am 11:55 AM
La technologie de détection et de reconnaissance des visages est déjà une technologie relativement mature et largement utilisée. Actuellement, le langage d'application Internet le plus utilisé est JS. La mise en œuvre de la détection et de la reconnaissance faciale sur le front-end Web présente des avantages et des inconvénients par rapport à la reconnaissance faciale back-end. Les avantages incluent la réduction de l'interaction réseau et de la reconnaissance en temps réel, ce qui réduit considérablement le temps d'attente des utilisateurs et améliore l'expérience utilisateur. Les inconvénients sont les suivants : il est limité par la taille du modèle et la précision est également limitée ; Comment utiliser js pour implémenter la détection de visage sur le web ? Afin de mettre en œuvre la reconnaissance faciale sur le Web, vous devez être familier avec les langages et technologies de programmation associés, tels que JavaScript, HTML, CSS, WebRTC, etc. Dans le même temps, vous devez également maîtriser les technologies pertinentes de vision par ordinateur et d’intelligence artificielle. Il convient de noter qu'en raison de la conception du côté Web
 Comment créer un graphique en chandeliers boursiers en utilisant PHP et JS
Dec 17, 2023 am 08:08 AM
Comment créer un graphique en chandeliers boursiers en utilisant PHP et JS
Dec 17, 2023 am 08:08 AM
Comment utiliser PHP et JS pour créer un graphique en bougies boursières. Un graphique en bougies boursières est un graphique d'analyse technique courant sur le marché boursier. Il aide les investisseurs à comprendre les actions de manière plus intuitive en dessinant des données telles que le prix d'ouverture, le prix de clôture, le prix le plus élevé et le prix le plus élevé. prix le plus bas des fluctuations du prix des actions. Cet article vous apprendra comment créer des graphiques en bougies boursières en utilisant PHP et JS, avec des exemples de code spécifiques. 1. Préparation Avant de commencer, nous devons préparer l'environnement suivant : 1. Un serveur exécutant PHP 2. Un navigateur prenant en charge HTML5 et Canvas 3.
 Outils essentiels pour l'analyse boursière : découvrez les étapes pour dessiner des graphiques en bougies avec PHP et JS
Dec 17, 2023 pm 06:55 PM
Outils essentiels pour l'analyse boursière : découvrez les étapes pour dessiner des graphiques en bougies avec PHP et JS
Dec 17, 2023 pm 06:55 PM
Outils essentiels pour l'analyse boursière : découvrez les étapes pour dessiner des graphiques en bougies en PHP et JS. Des exemples de code spécifiques sont nécessaires. Avec le développement rapide d'Internet et de la technologie, le trading d'actions est devenu l'un des moyens importants pour de nombreux investisseurs. L'analyse boursière est une partie importante de la prise de décision des investisseurs, et les graphiques en bougies sont largement utilisés dans l'analyse technique. Apprendre à dessiner des graphiques en bougies à l'aide de PHP et JS fournira aux investisseurs des informations plus intuitives pour les aider à prendre de meilleures décisions. Un graphique en chandeliers est un graphique technique qui affiche les cours des actions sous forme de chandeliers. Il montre le cours de l'action
 Comment utiliser JS et Baidu Map pour implémenter la fonction de traitement des événements de clic sur la carte
Nov 21, 2023 am 11:11 AM
Comment utiliser JS et Baidu Map pour implémenter la fonction de traitement des événements de clic sur la carte
Nov 21, 2023 am 11:11 AM
Présentation de la façon d'utiliser JS et Baidu Maps pour implémenter les fonctions de traitement des événements de clic sur la carte : dans le développement Web, il est souvent nécessaire d'utiliser des fonctions de carte pour afficher la localisation géographique et les informations géographiques. Le traitement des événements de clic sur la carte est une partie couramment utilisée et importante de la fonction de carte. Cet article explique comment utiliser JS et l'API Baidu Map pour implémenter la fonction de traitement des événements de clic de la carte et donne des exemples de code spécifiques. Étapes : Importez le fichier API de Baidu Map. Tout d’abord, importez le fichier de l’API Baidu Map dans le fichier HTML. Cela peut être réalisé via le code suivant :
 Comment utiliser JS et Baidu Maps pour implémenter la fonction de carte thermique de carte
Nov 21, 2023 am 09:33 AM
Comment utiliser JS et Baidu Maps pour implémenter la fonction de carte thermique de carte
Nov 21, 2023 am 09:33 AM
Comment utiliser JS et Baidu Maps pour implémenter la fonction de carte thermique de carte Introduction : Avec le développement rapide d'Internet et des appareils mobiles, les cartes sont devenues un scénario d'application courant. En tant que méthode d'affichage visuel, les cartes thermiques peuvent nous aider à comprendre la distribution des données de manière plus intuitive. Cet article explique comment utiliser JS et l'API Baidu Map pour implémenter la fonction de carte thermique de carte et fournit des exemples de code spécifiques. Travail de préparation : Avant de commencer, vous devez préparer les éléments suivants : un compte développeur Baidu, créer une application et obtenir l'AP correspondant
 Conseils de développement PHP et JS : maîtrisez la méthode de création de graphiques en bougies boursières
Dec 18, 2023 pm 03:39 PM
Conseils de développement PHP et JS : maîtrisez la méthode de création de graphiques en bougies boursières
Dec 18, 2023 pm 03:39 PM
Avec le développement rapide de la finance sur Internet, l'investissement en actions est devenu le choix de plus en plus de personnes. Dans le trading d'actions, les graphiques en bougies sont une méthode d'analyse technique couramment utilisée. Ils peuvent montrer l'évolution des cours des actions et aider les investisseurs à prendre des décisions plus précises. Cet article présentera les compétences de développement de PHP et JS, amènera les lecteurs à comprendre comment dessiner des graphiques en bougies boursières et fournira des exemples de code spécifiques. 1. Comprendre les graphiques en bougies boursières Avant de présenter comment dessiner des graphiques en bougies boursières, nous devons d'abord comprendre ce qu'est un graphique en bougies. Les graphiques en chandeliers ont été développés par les Japonais
 Comment utiliser JS et Baidu Maps pour implémenter la fonction de dessin de polygones de carte
Nov 21, 2023 am 10:53 AM
Comment utiliser JS et Baidu Maps pour implémenter la fonction de dessin de polygones de carte
Nov 21, 2023 am 10:53 AM
Comment utiliser JS et Baidu Maps pour implémenter la fonction de dessin de polygones cartographiques. Dans le développement Web moderne, les applications cartographiques sont devenues l'une des fonctions courantes. Dessiner des polygones sur la carte peut nous aider à marquer des zones spécifiques que les utilisateurs peuvent visualiser et analyser. Cet article explique comment utiliser JS et l'API Baidu Map pour implémenter la fonction de dessin de polygones de carte et fournit des exemples de code spécifiques. Tout d’abord, nous devons introduire l’API Baidu Map. Vous pouvez utiliser le code suivant pour importer le JavaScript de l'API Baidu Map dans un fichier HTML





